Некоторые вопросы нелинейной механики грунтов

Для стадии установившегося пластично-вязкого течения

t _i = t₀ + h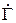, h = tgn (6.24)

Это и есть уравнение установившегося пластично-вязкого течения Бингама - Шведова, применимость которого к глинистым грунтам доказана опытами П.А.Ребиндера, Н.Н.Маслова, Н.М.Гольдштейна, Э.В.Костерина и многих других исследователей.

Теорию линейно-деформируемой среды можно применять для расчета осадок и напряжений, если под фундаментами происходит уплотнение грунтов и частично развиваются зоны местных сдвигов (пластические деформации) на глубину до 0,25 b (b - ширина фундамента). Если мы хотим проектировать фундаменты зданий и сооружений, исходя из предельно допустимых деформаций, особенно для тяжелых сооружений, необходимо использовать закономерности нелинейной механики. В этом случае напряженное состояние грунтов приходится рассматривать, например, по октаэдрическим площадкам, равнонаклонным к плоскостям, по которым действуют главные напряжения. Из общей механики сплошных сред известно, что на эти площадки будут действовать октаэдрические напряжения:

нормальные

(6.25)

и касательные

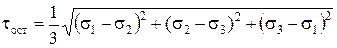. (6.26)

Кроме деформаций объема, большое значение имеют и деформации формы. За меру деформации формы принимают интенсивность деформаций сдвигов

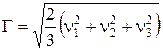, (6.27)

где – наибольшие главные деформации сдвигов. Деформации объема и формы могут быть выражены через s_ост и t_ост.

На рис.6.6 показаны графики зависимости деформации объема (а) и формы (б) от октаэдрических напряжений. Анализ этих графиков показывает, что линейную зависимость между напряжениями и деформациями можно использовать при небольших октаэдрических нормальных и касательных напряжениях. При увеличении напряжений следует учитывать нелинейную зависимость между напряжениями и деформациями.

Рис.6.6. Зависимость деформации объема (а) и формы (б) от октаэдрических напряжений. 1 – линейная зависимость между напряжениями и деформациями; 2 – экспериментальная кривая для случая неизменности объема; 3 – экспериментальные кривые при изменении объема в результате деформации сдвигов; 4 – кривые, которые соответствуют развитию деформации формы при различных октаэдрических нормальных напряжениях

На кафедре ОФиМ ПГТУ разработаны метод и программа прогноза напряженно-деформируемого состояния системы "основание - сооружение" с учетом нелинейного деформирования, предыстории нагружения массива и изменяющейся жесткости сооружения при строительстве [21].

Дата добавления: 2014-01-07