Кратчайший путь между парами вершин, транзитивное замыкание отношения

Очевидно, что задачу определения расстояния между всеми парами вершин можно решить, используя n раз (поочередно для каждой вершины) один из описанных ранее методов нахождения расстояний от фиксированной вершины. Таким образом мы получаем алгоритм со сложностью O(n⁴) (при использовании метода Форда-Беллмана) или O(n³) для бесконтурных графов или неотрицательных весов. Однако оказывается, что в общем случае n-кратное использование метода Форда-Беллмана не является лучшим методом. Покажем теперь два более эффективных метода.

Для этого рассмотрим ориентированный граф G=(V,E), где V={v₁,...,v_n }, и предположим, что А=[a_ij] есть матрица весов (a_ij=a(v_i,v_j)). Обозначив через d^(m)_ij длину кратчайшего пути из v_i и v_j, содержащего не более m дуг, получаем следующее очевидные уравнения(cp. c(3.3)):

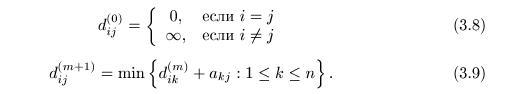
Отметим, что уравнение (3.9) обнаруживает некоторое сходство с определением произведения двух кратных матриц. Если операцию min трактовать как "сумму", операцию "+"- как "произведение", то матрица [d^(m)_ij] и А=[a_ij]. Обозначим такое "произведение" двух матриц А и В через A * B и отметим, что для этой операции единичным элементом служит матрица:

Из уравнений (3.9) и (3.9) теперь легко следует, что d⁽⁰⁾_ij=U и

1. d^(n-1)_ij=d⁽ⁿ⁾_ij и в результате d^(m)_ij=d^(n-1)_ij для каждого m=>n. Тогда очевидно d^(n-1)_ij= d(v _i ,v_j).
2.d^(n-1)_ij не равно d⁽ⁿ⁾_ij. Это означает, что существует контур отрицательной длины.
Произведение А * В двух матриц размерности n * n можно вычислить за время O(n³) (n сложений и n-1 сравнений на каждый из n² элементов произведения A * B). Следовательно, матрицу [d^(n-1)_ij] и тем самым расстояние между всеми парами вершин можно вычислить за время O(⁴).
Пока сложность этого алгоритма такая же, как и для случая n-кратного использования алгоритма Форда-Беллмана. Однако мы сможем ее снизить если заметим, что "*" ассоциативно. Этот факт позволяет вычислить произведение (3.10), поочередно возводя матрицу А в квадрат и тем самым заменяя n-1 умножение матрицы [log n] умножения. таким образом, мы получаем алгоритм сложности O(n³log n), отыскивающий расстояние между всеми парами вершин в графе без контуров отрицательной длины.
Авторами еще более эффективного алгоритма являются Уоршал[ 70 ] и Флойд [ 20 ]. Идея алгоритма следующая. Обозначим через d^(m)_ij длину кратчайшего из путей из v_i в v_j с промежуточными вершинами в множестве { v₁,...,v_m }. Тогда имеем следующие уравнения:
d ^o _ij = a_ij (3.11)
d^(m+1)_ij=min 'd^(m)_ij, d^(m)_im+d^(m)_mj' (3.12)
Обоснование второго уравнения достаточно простое. рассмотрим кратчайший путь не содержит v_m+1, то d^(m+1)_ij= d^(m)_ij. Если же он содержит v_m+1, то, деля путь на отрезки от v_i до v_m+1 и от v_m+1 до v_j, получаем равенство d^(m+1)_ij = d^(m)_im + d^(m)_mj.
Уравнения (3.11) и (3.12) дают возможность легко вычислить расстояния d(v_i,v_j) = d⁽ⁿ⁾_ij, 1<= i,j <=n.
Алгоритм 3.7. (Вычисление расстояний между всеми парами вершин - метод Флойда.)
Данные: Матрица весов дуг A[ i,j ], 1<= i,j <=n ориентированного графа без контуров отрицательной длины.
Результаты: Расстояния между всеми парами вершин D[ i,j ] = d(v_i,v_j).

1. begin
2. for i: =1 to n do
3. for j: = 1 to n do D[i,j]:= A[i,j];
4. for i:= 1 to n do D[i,j]:=0;
5. for m:= 1 to n do
6. for i:= 1 to n do
7. for j:= 1 to n do
8. D[i,j]:=min(D[i,j], D[i,m] + D[m,j])
9. end

Обоснование корректности алгоритма предоставляем читателю. Очевидно, что сложность этого алгоритма есть O(n₃). Стоит отметить, что такую же сложность имел алгоритм Форда-Беллмана нахождения расстояний от фиксированной вершины до всех остальных вершин. Любопытно, что для общего случая не известен ни один алгоритм нахождения расстояния между одной фиксированной парой вершин, который был бы значительно эффективнее алгоритма нахождения расстояний между всеми парами вершин.
С задачей определения кратчайших путей в графе тесно связана задача транзитивного замыкания бинарного отношения. Вспомним, что под бинарным отношением на множестве V мы понимаем произвольное подмножество E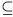V x V. Такое отношение является транзитивным, если удовлетворяется условие: (x,y) принадлежит E 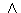(y,z) принадлежит E следовательно (x,z) принадлежат E
любых x,y,z принадлежащих E. Отметим, что бинарное отношение E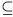V x V. Можно однозначно представить ориентированным графом G = (V, E). Для произвольного такого отношения мы определяем
E^*= { (x, y): в (V, E) существует путь ненулевой длины из x в y }.
Нетрудно заметить, что E^*- транзитивное отношение на множестве V и E содержащего E^*. Более того, E^* является наименьшим транзитивным отношением, содержащим Е. Отношение E^* является транзитивным замыканием отношения Е.
Если отношение Е представить виде графа (V, E), в котором каждая дуга имеет вес 1, то транзитивное замыкание E^* можно вычислить с помощью алгоритма (3.7) за время O(n₃); после завершения работы алгоритма имеем
(v_i, v_j) принадлежащие E^* равносильно D[ i, j ] < бесконечности.
При вычислении транзитивного замыкания удобно принять

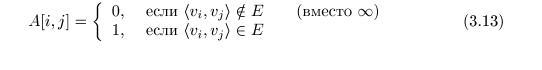
Тогда строку 7 алгоритма 3.7 мы можем заменить на
D[i,j]:= D[i, j] 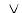(D[i, m],
где 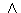и 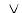обычные булевы операции:

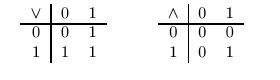
После завершения работы алгоритма, модифицированного таким образом, очевидно, имеем

Здесь следует отметить, что известен алгоритм построения транзитивного замыкания, более эффективный, чем алгоритм Уоршала (см. [53]). Он использует связь этой задачи с умножением матриц, обсуждавшуюся в начале этого параграфа, эта связь для матриц А, определяемых равенством (3.13), приводит к обычному умножению булевых матриц по формуле

Оказывается (см. [64]), что такое умножение выполнить за время O(n^log7)1, что дает алгоритм построения транзитивного замыкания, имеющего сложность O(n^log7logn). Такой алгоритм имеет скорее теоретическое значение, поскольку метод умножения матриц за время O(n^log7) является довольно сложным и, следовательно, обнаруживает свое преимущество перед обычным "школьным" методом только при очень больших значениях n. На практике обычно самым эффективным оказывается алгоритм Уоршала, соответствующим образом запрограммированный (см. [65] и задачу 3.9).
Другим способом построения транзитивного замыкания отношения Е является применение поиска в глубину (или в ширину) в графе (V,E). Этот способ особенно выгоден, когда отношение Е симметрично; очевидно, что тогда транзитивное замыкание строится отдельно для каждой связной компоненты, на которые разбивается неориентированный граф, определяемый отношением Е, и это построение может быть получено за время O(m+n). Детали оставляем читателю (см. задачу 3.12).

Дата добавления: 2014-01-07