Машинное представление графов

Очевидно, что наиболее понятный и полезный для человека способ представления графа - изображение графа на плоскости в виде точек и соединяющих их линий - будет совершенно бесполезным, если мы захотим решать с помощью ЭВМ задачи, связанные с графами.

Выбор соответствующей структуры данных для представления графа имеет принципиальное влияние на эффективность алгоритмов, поэтому мы подробнее остановимся на данной проблеме. Мы покажем несколько различных способов представления и кратко разберем их достоинства и недостатки.

Мы будем рассматривать как ориентированные, так и неориентированные графы. Граф мы всегда будем обозначать G = (V, E), где V обозначает множество вершин, а E множество ребер.

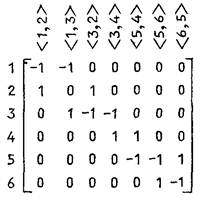
В теории графов классическим способом представления графов служит матрица инциденций. Это матрица A c n строками, соответствующими вершинам, и m столбцами, соответствующими ребрам. Для ориентированного графа столбец, соответствующий дуге < x, y > содержит -1 в строке, соответствующей вершине x, 1 в строке соответствующей вершине y, и нулю во всех остальных строках. Петлю, т.е. дугу вида < x, x > удобно представлять иным значением в строке x, например 2. В случае неориентированного графа столбец, соответствующий ребру { x, y }, содержит 1 в строках, соответствующих x и y, и нули в остальных строках.

a) Ориентированный граф и его матрица инциденций

б) Неориентированный граф и его матрица инциденций

С алгоритмической точки зрения матрица инциденций является, вероятно, самым худшим способом представления графа, который только можно себе представить. Во-первых, он требует nm ячеек, причем большинство этих ячеек вообще занято нулями. Неудобен также доступ к информации. Ответ на элементарные вопросы типа «существует ли дуга < x, y >?», к каким вершинам ведут ребра их x?» требует в худшем случае перебора всех столбцов матрицы, а следовательно, m шагов.

Лучшим способом представления графа является матрица смежности, определяемая как B = [b_ij] размера n x n, где b_ij=1, если существует ребро идущее из вершины x в вершину y, и b_ij=0 в противном случае. Здесь мы подразумеваем, что ребро { x, y } неориентированного графа идет как от x к y, так и от y к x, так что матрица такого графа является всегда симметричной.

a) Ориентированный граф и его матрица смежности

б) Неориентированный граф и его матрица смежности

Основным преимуществом матрицы смежности является тот факт, что за один шаг можно получить ответ на вопрос «существует ли дуга из x в y?». Недостатком же является тот факт, что независимо от числа ребер объем занятой памяти составляет n ².

На практике это неудобство можно иногда уменьшить, храня целую строку (столбец) матрицы в одном машинном слове – это возможно для малых n.

Дата добавления: 2014-01-07