Метод интегрирования по частям

Пусть u=u(x) и v=v(x) – дифференцируемые функции. По свойству дифференциала d(uv)=vdu+udv или udv= d(uv)-vdu. Интегрируя левую и правую части равенства получаем:

.

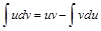(6)

Формула (6) называется формулой интегрирования по частям для неопределенного интеграла. При ее применении фиксируется разбиение подынетгрального выражения на два сомножителя (u и dv). При переходе к правой части равенства (6) первый из них дифференцируется, а второй интегрируется. Выбор сомножителей осуществляется сходя из условия, что дифференцирование упрощает первый сомножитель, а интегрирование не слишком усложняет другой.

Наиболее часто встречающиеся виды интегралов, которые находятся методом интегрирования по частяим, можно разбить на две группы:

I	II
,,	,,, ,

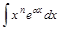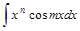
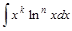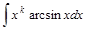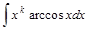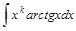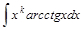
a,m,k – действительные числа (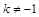), n – целое положительное число.

Для нахождения интегралов из первой группы формулу интегрирования по частям придется применить n раз, пока степень n переменной x не станет равной нулю. При этом принимают 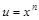, остальные сомножители подынтегрального выражения задают равными dv.

Для нахождения интегралов второй группы полагают 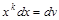, оставшиеся сомножители задают выражения для u.

Замечание. Константа C, полученная при вычислении v в запись окончательного ответа не входит. Поэтому при подстановке ее в формулу (6) будем принимать C=0, что упростит запись решения.

На практике метод интегрирования по частям часто комбинируется с другими методами интегрирования.

Пример 1. Найти интеграл: .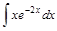

Решение: 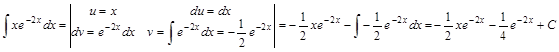Пример 2. Найти интеграл: .

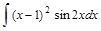Решение:

.

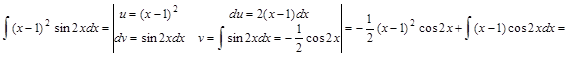
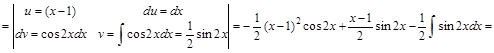
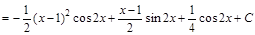Пример 3. Найти интеграл: .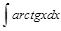

Решение: .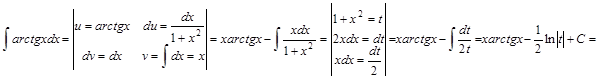

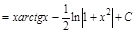Пример 4. Найти интеграл: .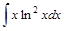

Решение: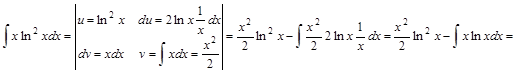

.

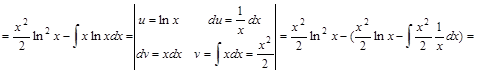
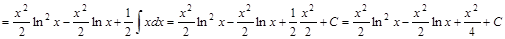Интегралы вида 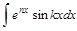и 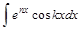называются возвратными интегралами. Они также находятся методом интегрирования по частям за счет того, что операции дифференцирования и интегрирования не меняют множитель 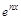с точностью до постоянного коэффициента n, а после двойного интегрирования или дифференцирования множитель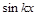или 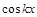возвращается к своему исходному виду, но с обратным знаком и с точностью до постоянного коэффициента k.

Пример 5. Вычислить возвратный интеграл: .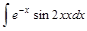

Решение.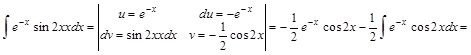

.

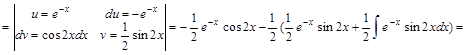
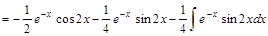Как видно из примера, после второго применения метода интегрирования по частям был получен исходный интеграл. Обозначим его и решим полученное функциональное уравнение относительно :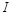

;

;

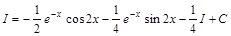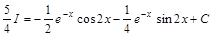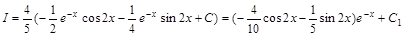, где .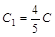

Таким образом данный возвратный интеграл равен .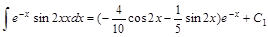

Дата добавления: 2014-01-07