Основные понятия

Элементы теории обыкновенных дифференциальных уравнений

Определение. Дифференциальным уравнением (сокращенно ДУ) называется уравнение, в которую входит неизвестная функция вместе со своими аргументами и производными различных порядков данной функции.

Если функция зависит от одной переменной, то такие уравнения называются обыкновенными, если от нескольких, то уравнениями в частных производных. Мы будем рассматривать только обыкновенные дифференциальные уравнения.

В общем случае дифференциальное уравнение можно записать в виде:

,

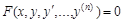(1)

где F – некоторая функция от n+2 переменных.

Порядок n старшей производной, входящей в запись дифференциального уравнения называется порядком дифференциального уравнения.

Например, 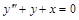- ДУ 3 порядка.

Дифференциальное уравнение n-го порядка называется разрешенным относительно старшей производной, если оно имеет вид:

,

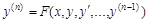(2)

где F – некоторая функция от (n+1) переменной.

Определение: Решением дифференциального уравнения (1) называется такая функция 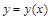, которая при подстановке ее в это уравнение обращает его в тождество.

Пример 1. Функция 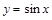является решением уравнения , так как 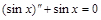при любых значениях x.

Задача о нахождении решения некоторого дифференциального уравнения называется задачей интегрирования данного дифференциального уравнения.

График решения дифференциального уравнения называется интегральной кривой.

Определение. Общим решением дифференциального уравнения n-го порядка называется такое его решение вида

,

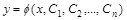(3)

которое является функцией переменной x и n произвольных независимых постоянных .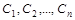

Определение. Частным решением дифференциального уравнения называется решение, получаемое из общего решения при некоторых конкретных числовых значениях постоянных .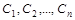

К дифференциальным уравнениям приводит ряд задач экономики, физики, биологии, экологии и других наук.

Пример 2. Из статистических данных известно, что прирост населения некоторого города составляет 5% в год. Найти закон изменения численности населения города и количество жителей через 10 лет, если известно, что в настоящий момент в городе проживает 10 000 человек.

Решение: Пусть 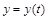-функция, показывающая зависимость численности жителей от времени, k=0.05 – прирост населения, где 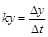. Перейдем к пределу при :

.

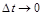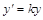Решаем данное дифференциальное уравнение:

; ; ; проинтегрируем обе части равенства: ;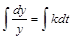

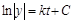; выразим y: 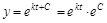; обозначим константу ;

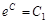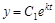- общее решение дифференциального уравнения.

Чтобы определеить, сколько человек будет жить в городе через десять лет, нужно знать, сколько их живет в некоторый известный момент времени. По условию задачи сказано, что .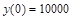

;

.

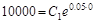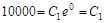Частное решение данного уравнения: .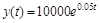

Через десять лет в городе будет проживать: 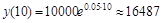человек.

Дата добавления: 2014-01-07