Для функций

Рассмотрим функцию 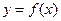, которая точке 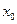имеет все необходимые производные.

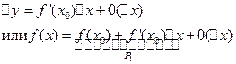
Многочлен 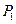дает приближение функции на величину 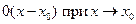. Многочлен 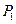обладает свойством, что его значение в точке 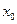и первая производная в точке 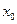совпадают с таковыми для самой функции. Возникает гипотеза, что многочлен 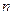-ного порядка 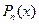даст еще большее приближение нашей функции, причем значение этого многочлена 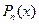и его производной в точке 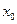совпадает с таковыми для самой функции.

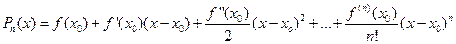(4) – многочлен Тейлора 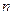-ной степени для функции 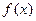с центром в точке.

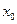Обозначая 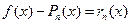, можно записать: 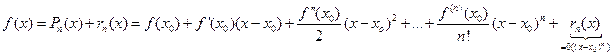(5)- формула Тейлора 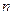-ной степени для функции 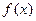с центром в точке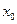и остаточным членом .

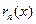Замечание. Записывая 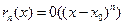, говорят, что остаточный член записан в форме Пеано. Формула Тейлора для функции при 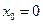называют формулой Маклорена:

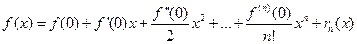
Лекция №12.

§6.6. Приложения формулы Тейлора.

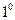Для разложения некоторых функций (все разложения будут рассматриваться по формуле Маклорана, т.е. при ).

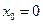1)

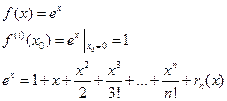
2)

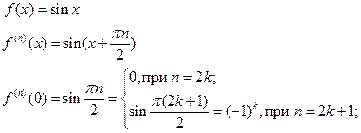
В разложении будут отсутствовать четные номера производных, а нечетные будут чередоваться, начиная с +1.

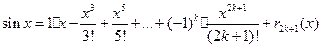
3)

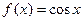
В разложении будут отсутствовать нечетные номера, а четные будут чередоваться, начиная с +1.

4)

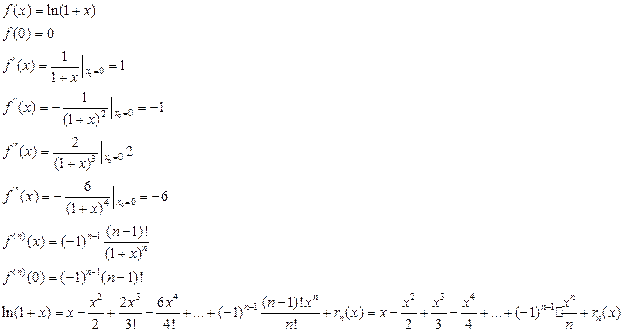
5) Биноминальное разложение

Если 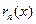в полученных формулах взять в виде 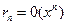(в форме Пиана), то увидим, что все они дают нам более точные, чем известные нам ранее выражения эквивалентности для функций 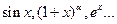, приближения.

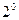Для вычисления некоторых функций.

При разложении формул Тейлора можно оценить погрешность этой формулы, т.л. она равна (по абсолютной величине) первому отброшенному члену.

Например:

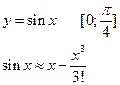
определяем погрешность

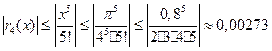
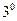Для вычисления пределов.

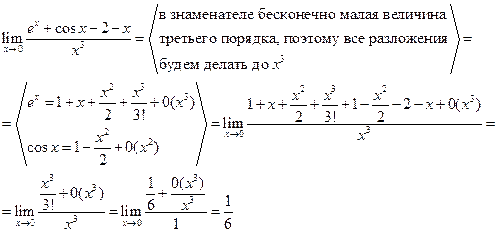
Дата добавления: 2014-01-06