
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Приклад 1
|
|
|
|
Задача про використання сировини
З математичної точки зору ця задача є узагальненням тієї, котра розглянута в попередньому параграфі. Формулюється вона так.
Підприємство випускає продукцію n видів  , на виготовлення якої витрачається сировина m видів
, на виготовлення якої витрачається сировина m видів 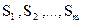 , запаси котрої на підприємстві дорівнюють відповідно
, запаси котрої на підприємстві дорівнюють відповідно 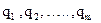 . Відомі витрати
. Відомі витрати 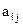 сировини Si на виробництво одиниці продукції
сировини Si на виробництво одиниці продукції  (i =
(i = 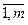 ; j =
; j = ). Вартість одиниці продукції
). Вартість одиниці продукції  дорівнює
дорівнює  (j =
(j = ). Потрібно скласти такий план випуску продукції, при якому прибуток від реалізації продукції був би найбільшим.
). Потрібно скласти такий план випуску продукції, при якому прибуток від реалізації продукції був би найбільшим.
Складемо математичну модель задачі.
Нехай 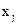 - кількість одиниць продукції
- кількість одиниць продукції  (j =
(j = ).
).
Математична модель має вигляд:
f =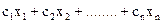 → max
→ max
при обмеженнях:
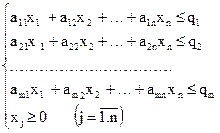 (4.0)
(4.0)
4.3. Задачі складання раціону (задача про дієту)
Для відгодівлі тварини використовується n видів кормів, що містять m видів поживних речовин. Нехай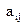 - вміст i- ої поживної речовини в одному кілограмі j - го виду корму
- вміст i- ої поживної речовини в одному кілограмі j - го виду корму 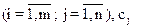 - вартість одного кілограма j-ro виду корму
- вартість одного кілограма j-ro виду корму 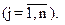 Мінімальна добова потреба тварини в i-ої поживній речовині дорівнює
Мінімальна добова потреба тварини в i-ої поживній речовині дорівнює  . Необхідно скласти найбільш дешевий раціон потрібної поживності.
. Необхідно скласти найбільш дешевий раціон потрібної поживності.
Позначимо через xj кількість кілограмів корму j-го виду.
Очевидно, математична модель задачі така.
f =  → min
→ min
при обмеженнях:
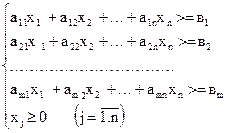
4.4. Загальна постановка задач лінійного програмування
Лінійним обмеженням, накладеним на змінні  , називається співвідношення одного з наступних трьох типів:
, називається співвідношення одного з наступних трьох типів:
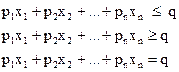
де  - дійсні числа.
- дійсні числа.
Наприклад, співвідношення 2х -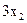 ≤ 1 або
≤ 1 або 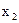 ≥ 0 є
≥ 0 є
лінійними, а співвідношення  ≥ 3 або sin x1 ≤
≥ 3 або sin x1 ≤  не є лінійними.
не є лінійними.
Загальна постановка задачі лінійного програмування (ЗЛП) полягає в наступному.
Дано деяку лінійну функцію
f = n (4.1)
n (4.1)
і деяка система лінійних обмежень, накладених на змінні 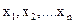 :
:
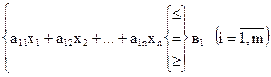 (4.2)
(4.2)
Потрібно знайти такі значення змінних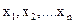 , які
, які
задовольняли б обмеженням (4.2) і при цьому обертали б в оптимум (max і min) функцію (4.1).
Функція (4.1) називається цільовою. Кожний набір значень змінних, при яких задовольняються обмеження (4.2), називається припустимим рішенням або припустимим планом ЗЛП. Сукупність всіх припустимих рішень називається областю припустимих рішень (ОПР).
Наведені в параграфах 4.1, 4.2, 4.3 задачі є задачами лінійного програмування.
Припустиме рішення, що обертає цільову функцію в оптимум, називається оптимальним рішенням або оптимальним планом.
Говорять, що ЗЛП розв'язна, якщо вона має оптимальний план. У протилежному випадку задача називається нерозв'язною.
ЗЛП може бути нерозв'язною тільки з наступних двох причин:
а) ОПР порожня;
б) ОПР непорожня, але цільова функція не обмежена на ОПР зверху, якщо в ЗЛП шукається її максимум, або - не обмежена знизу, якщо в ЗЛП шукається мінімум цільової функції.
Наприклад, задача: f =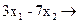 min
min
при обмеженнях

нерозв'язна через порожнечу ОПР.
Задача ж f = max при обмеженні
max при обмеженні
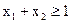 нерозв'язна через те, що цільова функція не обмежена зверху на ОПР. (Щоб переконатися в цьому, розгляньте такі припустимі рішення:
нерозв'язна через те, що цільова функція не обмежена зверху на ОПР. (Щоб переконатися в цьому, розгляньте такі припустимі рішення: 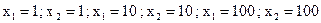 і т.д.).
і т.д.).
5. ГЕОМЕТРИЧНИЙ МЕТОД ВИРІШЕННЯ ЗЛП
У випадку, коли число змінних у ЗЛП дорівнює двом, завдання можна вирішити геометрично. Розглянемо приклади.
f = 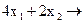 max
max
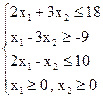
Кожне припустиме рішення ЗЛП будемо зображувати точкою 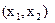 координатної площини. Побудуємо ОПР (рис. 5.1). Розглянемо перше лінійне обмеження
координатної площини. Побудуємо ОПР (рис. 5.1). Розглянемо перше лінійне обмеження  . Сукупність точок площини, що задовольняють цьому обмеженню, являє собою напівплощину, обмежену прямою
. Сукупність точок площини, що задовольняють цьому обмеженню, являє собою напівплощину, обмежену прямою 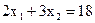 . Спочатку побудуємо цю граничну пряму (її можна побудувати по двох точках: (0,6) і (9,0). Ця пряма розіб'є площину на дві напівплощини. Щоб вирішити питання про те, яку із цих двох напівплощин визначає нерівність
. Спочатку побудуємо цю граничну пряму (її можна побудувати по двох точках: (0,6) і (9,0). Ця пряма розіб'є площину на дві напівплощини. Щоб вирішити питання про те, яку із цих двох напівплощин визначає нерівність  , візьмемо в одній з напівплощин яку-небудь точку, що не лежить на граничній прямій, і підставимо її координати в нерівність. Наприклад, за таку точку візьмемо початок координат - точку (0,0). Оскільки
, візьмемо в одній з напівплощин яку-небудь точку, що не лежить на граничній прямій, і підставимо її координати в нерівність. Наприклад, за таку точку візьмемо початок координат - точку (0,0). Оскільки  , то напівплощина, обумовлена нерівністю
, то напівплощина, обумовлена нерівністю  , містить точку (0,0). Аналогічно знаходимо напівплощини, обумовлені іншими обмеженнями. Далі визначимо ОПР як загальну частину отриманих напівплощин. Одержимо опуклий багатокутник
, містить точку (0,0). Аналогічно знаходимо напівплощини, обумовлені іншими обмеженнями. Далі визначимо ОПР як загальну частину отриманих напівплощин. Одержимо опуклий багатокутник

Рис.5.1.
Тепер залишилося визначити максимум цільової функції на ОПР. Для цього побудуємо лінії рівня цільової функції. Лінія рівня - це безліч точок площини, у яких цільова функція приймає постійне значення. Оскільки цільова функція
f =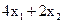 ,то кожна лінія рівня має вигляд
,то кожна лінія рівня має вигляд . Бачимо, що при різних значеннях параметра С маємо паралельні прямі. Побудуємо, наприклад, дві лінії рівня, поклавши С = 4 і С = 8. Відзначимо стрілкою напрямок, у якому переміщається лінія рівня при збільшенні С. Пересуваючи лінію рівня в зазначеному напрямку, знайдемо точку ОПР, у якій С має найбільше значення. Це буде точка А. Вона є результатом перетинання двох прямих:
. Бачимо, що при різних значеннях параметра С маємо паралельні прямі. Побудуємо, наприклад, дві лінії рівня, поклавши С = 4 і С = 8. Відзначимо стрілкою напрямок, у якому переміщається лінія рівня при збільшенні С. Пересуваючи лінію рівня в зазначеному напрямку, знайдемо точку ОПР, у якій С має найбільше значення. Це буде точка А. Вона є результатом перетинання двох прямих: 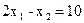 і
і 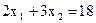
Для знаходження координат точки А вирішимо систему

Одержимо оптимальне рішення
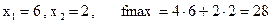
Приклад 2. f = min
min
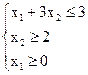


рис. 5.2.
У цьому прикладі напівплощини, обумовлені лінійними обмеженнями, не мають загальних точок. Тому ЗЛП нерозв'язна через порожнечу ОПР.
Приклад 3. f =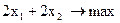

У даному прикладі (рис.5.3) ОПР - опукла необмежена багатокутна область.

рис. 5.3.
Побудуємо лінію рівня  . Пересуваючи лінію рівня в напрямку, зазначеному стрілкою, бачимо, що на ОПР цільова функція може приймати які завгодно великі значення. Тому ЗЛП нерозв'язна через необмеженість зверху на ОПР цільової функції.
. Пересуваючи лінію рівня в напрямку, зазначеному стрілкою, бачимо, що на ОПР цільова функція може приймати які завгодно великі значення. Тому ЗЛП нерозв'язна через необмеженість зверху на ОПР цільової функції.
Приклад 4. f =
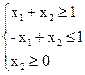
Цей приклад відрізняється від попереднього тільки тим, що цільову функцію потрібно мінімізувати, а не максимізувати. Лінію рівня потрібно переміщати в напрямку, протилежному тому, що зазначено на рисунку 5.3 стрілкою. Оскільки лінія рівня паралельна прямій 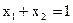 , то мінімальне значення на ОПР цільова функція досягає у всіх точках відрізка АВ. Щоб указати конкретне оптимальне рішення задачі, потрібно виписати координати якої-небудь точки цього відрізка.
, то мінімальне значення на ОПР цільова функція досягає у всіх точках відрізка АВ. Щоб указати конкретне оптимальне рішення задачі, потрібно виписати координати якої-небудь точки цього відрізка.
Наприклад,

Приклад 5. Вирішимо геометрично задачу про використання
обладнання, що розглядалася в параграфі 4.1. Її математична модель
f =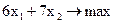

Побудуємо ОПР (рис 5.4). Потім проведемо лінію рівня  . Укажемо стрілкою напрямок, у якому переміщається лінія рівня
. Укажемо стрілкою напрямок, у якому переміщається лінія рівня  із збільшенням C. Максимум цільової функції на ОПР досягається в точці А. Для відшукання координат точки А вирішимо систему:
із збільшенням C. Максимум цільової функції на ОПР досягається в точці А. Для відшукання координат точки А вирішимо систему:

рис.5.4.
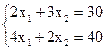
Звідси 
Відповідь. Оптимальний план такий: виробів А потрібно робити 7,5 одиниць, виробів В -5 одиниць; при цьому прибуток буде дорівнювати 80 грошовим одиницям.
Геометричний метод можна використовувати для вирішення ЗЛП із числом змінних n = 3. При більшому числі змінних ЗЛП не допускає наочного геометричного вирішення. Разом з тим для довільного числа змінних справедливі твердження:
1) область припустимих рішень являє собою опуклий багатогранник;
2) якщо ЗЛП розв'язна, то оптимальне рішення досягається в одній з вершин опуклого багатогранника.
6. ТАБЛИЧНИЙ ПРОЦЕСОР Excel У РІШЕННІ ЗАДАЧ ЛІНІЙНОГО ПРОГРАМУВАННЯ
При рішенні проблем в економіці часто розглядаються завдання знаходження точок, у яких досягаються максимальні або мінімальні значення функцій декількох змінних з лінійними й нелінійними обмеженнями. Іншими словами - знаходиться оптимальне рішення завдання управління з обмеженнями.
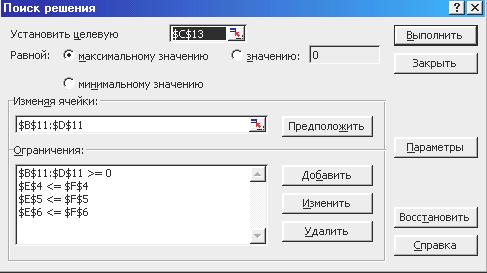
Всі завдання цього типу вирішуються за допомогою інструмента Excel Пошук рішення. Цей режим викликається за допомогою пунктів меню Сервис\Поиск решения, при цьому на екрані виникає вікно наступного виду:
У поле введення Установить целевую ячейку вказується посилання на комірку із цільовою функцією, значення якої буде максимальним, мінімальним або нулем залежно від обраного перемикача. Ця комірка повинна містити формулу. Кнопка Равной служить для вибору варіанта із заданим значенням цільової комірки. Щоб установити задане число, введіть його в поле.
Поле Изменяя ячейки служить для вказівки комірок, значення яких змінюються в процесі пошуку рішення доти, поки не будуть виконані накладені обмеження й умова оптимізації значення комірки, зазначеної в полі Установить целевую ячейку. У поле Изменяя ячейки вводяться імена або адреси змінюваних комірок. Поле Предположить використовується для автоматичного пошуку комірок, що впливають на формулу, посилання на яку дані в полі Установить целевую ячейку. Результат пошуку відображається в полі Изменяя ячейки.
Поля Ограничения служать для відображення списку граничних умов поставленого завдання. Система обмежень організується шляхом вказівки на комірки із записаними формулами командами Добавить, Изменить, Удалить. При цьому необхідно вказати вид порівняння за допомогою вікна введення обмежень (рис. 6.1), у якому є присутнім посилання на комірку з формулою обмеження, знак порівняння. У поле Ссылка на ячейку вводяться адреси комірок або діапазону, на значення яких накладаються обмеження. Зі списку, що розкривається, вибирається умовний оператор, який необхідно розмістити між посиланням і його обмеженням. Щоб приступити до набору нової умови, натисніть кнопку Додати.
Команда Выполнить служить для запуску пошуку рішення поставленого завдання. Команда Закрыть служить для виходу з вікна діалогу без запуску пошуку рішення поставленого завдання. При цьому зберігаються установи, зроблені у вікнах діалогу, що з'являлися після натискань на кнопки Параметры, Добавить, Заменить або Удалить.
Кнопка Параметры служить для відображення діалогового вікна Параметры поиска решения, у якому можна завантажити або зберегти модель, яка оптимізується і вказати передбачені варіанти пошуку рішення.
Кнопка Отмена служить для очищення полів вікна діалогу й відновлення значень параметрів пошуку рішення, використовуваних за замовчуванням.
 |
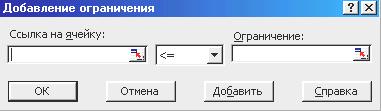 |
Рис. 6.1- Вид вікна в режимі Поиск решения
Рис.6.2.- Діалогове вікно Добавление ограничений
Настроювання параметрів алгоритму й програми проводиться в діалоговому вікні Параметры поиска решения ( рис.6.3). У вікні установлюються обмеження на час рішення завдань, вибираються алгоритми, задається точність рішення, надається можливість для збереження варіантів моделі і їхнього наступного завантаження. Значення й стани елементів управління, використовувані за замовчуванням, підходять для рішення більшості завдань.
Поле Максимальное время служить для обмеження часу, що відпускається на пошук рішення завдання. У поле можна ввести час (у секундах) не перевищуючий 32767; значення 100, використовуване за замовчуванням, підходить для рішення більшості лабораторних робіт.
Поле Предельное число итераций служить для управління часом рішення завдання, шляхом обмеження числа проміжних обчислень. У поле можна ввести час (у секундах) не перевищуючий 32767. При досягненні відведеного тимчасового інтервалу або при виконанні відведеного числа ітерацій на екрані з'являється діалогове вікно Текущее состояние поиска решения.
Поле Относительная погрешность служить для завдання точності (припустимої погрішності), з якої визначається відповідність комірки цільовому значенню або наближення до зазначених границь. Поле повинно містити число з інтервалу від 0 (нуля) до 1, наприклад, 0,0001. Висока точність збільшить час, потрібний для того, щоб зійшовся процес оптимізації. Чим менше введене число, тим вища точність результатів
Поле Допустимое отклонение служить для завдання допуску на відхилення від оптимального рішення. При вказівці більшого допуску пошук рішення закінчується швидше.
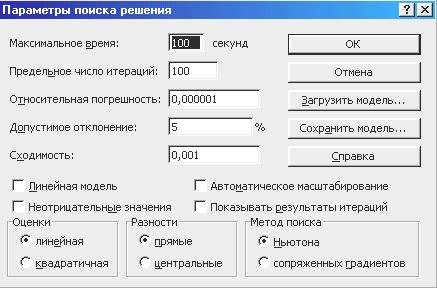 |
Рис. 6.3 - Діалогове вікно Параметры поиска решения
Поле Сходимость результатів пошуку рішення застосовується тільки до нелінійних завдань. Коли відносна зміна значення в цільовій комірці за останні п'ять ітерацій стає менше числа, зазначеного в полі Сходимость, пошук припиняється.
Прапорець Линейная модель служить для прискорення пошуку рішення лінійного завдання оптимізації або лінійної апроксимації нелінійного завдання.
Прапорець Неотрицательные значения дозволяє установити нульову нижню межу для тих комырок, для яких вона не була зазначена в поле Оганичения діалоговоговікна Добавление ограничения.
Прапорець Автоматическое масштабирование служить для включення автоматичної нормалізації вхідних і вихідних значень, що різняться за величиною, наприклад, максимізація прибутку у відсотках стосовно вкладень, обчислюваних у мільйонах рублів.
Прапорець Показывать результаты итераций служить для припинення пошуку рішення для перегляду результатів окремих ітерацій.
Кнопки Оценки служать для вказівки методу екстраполяції (лінійна або квадратична), використовуваного для одержання вихідних оцінок значень змінних у кожному одновимірному пошуку. Линейная служить для використання лінійної екстраполяції уздовж дотичного вектора. Кавдратичная служить для використання квадратичної екстраполяції, що дає кращі результати при рішенні нелінійних завдань.
Кнопки Разности (похідні) служать для вказівки методу чисельного диференціювання (прямі або центральні похідні), що використовується для обчислення часток похідних цільових і обмежуючих функцій. Прямые використовується для гладких безперервних функцій. Центральные використовується для функцій, що мають розривну похідну. Незважаючи на те, що даний спосіб вимагає більше обчислень, він може допомогти при одержанні підсумкового повідомлення про те, що процедура пошуку рішення не може поліпшити поточний набір вживаючих осередків.
Кнопки Метод поиска служать для вибору алгоритму оптимізації (метод Ньютона або сполучених градієнтів) – при необхідності. Кнопка Ньютона служить для реалізації квазіньютонівского методу, у якому запитується більше пам'яті, але виконується менше ітерацій, чим у методі сполучених градієнтів. Тут обчислюються частки похідні другого порядку. Кнопка Сопряженных градиентов служить для реалізації методу сполучених градієнтів, у якому запитується менше пам'яті, але виконується більше ітерацій, чим у методі Ньютона. Даний метод варто використовувати, якщо завдання досить велике й необхідно заощаджувати пам'ять, а також якщо ітерації дають занадто малу відмінність у послідовних наближеннях. Для рішення лінійних завдань використовуються алгоритми симплексного методу.
Команда Загрузить модель служить для відображення на екрані діалогового вікна Загрузить модель, у якому можна задати посилання на область комірок, призначену для зберігання моделі оптимізації. Даний варіант передбачений для зберігання на аркуші більше однієї моделі оптимізації. Перша модель зберігається автоматично.
Для прикладу розглянемо наступне завдання: меблева фабрика випускає три види продукції: столи, стільці й дивани, використовуючи при цьому три види ресурсів: дошки, цвяхи й клей. Відомі питомі витрати ресурсів, їхні запаси й прибуток, одержуваний від реалізації одиниці продукції:
| Стіл | Стілець | Диван | Запас | |
| Дошки | ||||
| Цвяхи | ||||
| Клей | ||||
| Прибуток |
Побудуємо математичну модель завдання знаходження оптимального плану. Позначимо xi, i=1,2,3, відповідно обсяги випуску столів, стільців і диванів. Тоді завдання максимізації прибутку буде виглядати в такий спосіб: знайти
20x1+18x2+22x3 ® max
за умови дотримання наступних обмежень:
9x1+5x2+6x3 £ 600
4x1+5x2+6x3 £ 400
3x1+4x2+5x3 £ 800
x1³0, x2³0, x3³0
Рішення поставленого завдання проведемо в табличному процесорі Excel за допомогою режиму «Поиск решения». Вихідні дані завдання оптимізації прибутку:
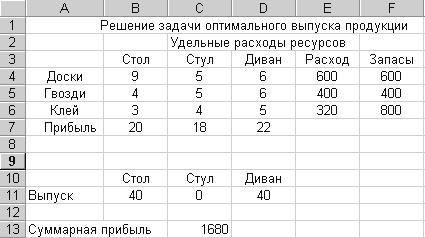 |
Рис.6.4 - Результат пошуку оптимального рішення
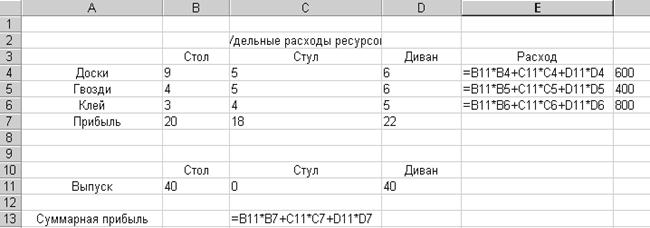 |
Використовувані в таблиці формули наступні:
Рис.6.5 - Формули, які введені для пошуку рішення
7. ЦІЛОЧИСЛОВЕ ЛІНІЙНЕ ПРОГРАМУВАННЯ
Цілочислове програмування - розділ математичного програмування, що розглядає оптимізаційні задачі, в яких всі або деякі змінні можуть приймати тільки цілі значення. Як правило, вимога цілочисельности змінних значно ускладнює задачу. Цілочислове програмування систематично вивчається з 1956 року, але й зараз цей розділ перебуває в стадії розвитку.
7.1. Загальна постановка задачі цілочислового лінійного програмування (ЗЦП)
Ми будемо розглядати тільки повністю цілочислові задачі, в яких вимога цілочисельності накладена на всі змінні. Загальний вигляд такої ЗЦЛП відрізняється від ЗЛП тільки тим, що до всіх змінних ставиться вимога цілочисельности. Зокрема, у канонічному вигляді ЗЦЛП ставиться так:
 (7.1)
(7.1)
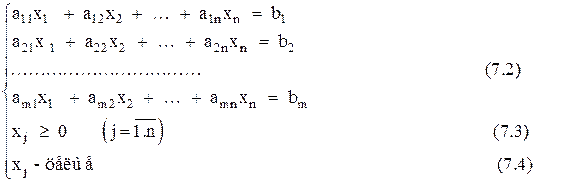
Для ЗЦЛП використовується саме така ж термінологія, що й для ЗЛП: цільова функція, припустиме рішення, оптимальне рішення тощо. Якщо в ЗЦЛП відкинути вимогу цілочисельності, то вийде так звана послаблена задача. Послаблена задача є ЗЛП, у той час як ЗЦЛП такою не є. Справа в тому, що вимога цілочисельності змінних не можна записати у вигляді лінійного обмеження. Аналітично його записати можна. Дійсно, позначимо через [a] цілу частину числа а, тобто найбільше ціле, що не більше а. Наприклад, [3.4] =3; [-7.2]= -8. Вимога цілочисельності змінної xj можна записати так: xj -[xj ] =0. Однак це співвідношення не є лінійним. Таким чином, не можна сказати, що ЗЦЛП є окремий випадок ЗЛП - вона взагалі не є ЗЛП.
З точних методів вирішення відзначимо геметричний метод (при двох змінних), метод відсікання Гоморі й комбінований метод гілок та меж.
На практиці більшість ЗЦЛП вирішується приблизно. При цьому часто доводиться розробляти наближений метод, що враховує специфічні особливості задачі.
Наведемо приклади ЗЦЛП.
7.2. Цілочислова задача про використання сировини
Підприємство випускає n видів штучної продукції вартістю 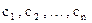 за штуку. Для виготовлення продукції використовується m видів сировини, запаси якої на підприємстві рівні відповідно
за штуку. Для виготовлення продукції використовується m видів сировини, запаси якої на підприємстві рівні відповідно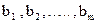 . Відома (m х n) – матриця (aij), в якій
. Відома (m х n) – матриця (aij), в якій 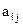 - витрата i – ої сировини на виробництво одиниці продукції j -го виду. Потрібно скласти такий план виробництва, при якому прибуток від реалізації продукції був б найбільшим.
- витрата i – ої сировини на виробництво одиниці продукції j -го виду. Потрібно скласти такий план виробництва, при якому прибуток від реалізації продукції був б найбільшим.
Математична модель задачі має вигляд:
f =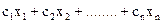 → max
→ max
при обмеженнях:
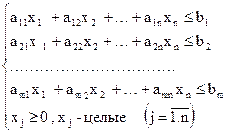
Тут 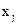 - кількість продукції j -го виду.
- кількість продукції j -го виду.
Це задача цілочислового лінійного програмування.
Цілочисельність змінних суттєва в тих випадках, коли мова йде про виробництво цінної продукції.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 809; Нарушение авторских прав?; Мы поможем в написании вашей работы!