Загальна характеристика й основні етапи симплекс - методу

СИМПЛЕКСНИЙ МЕТОД ВИРІШЕННЯ ЗЛП

Основоположниками симплекс-методу є радянський математик Л.В. Канторович і американський математик Дж. Данциг.

Симплекс-методом можна вирішити будь-яку ЗЛП або виявити її нерозв'язність. Багато спеціальних класів ЗЛП можна вирішити іншими, більш ефективними для цих класів методами. Однак перевага симплекс-методу - його універсальність. Майже для всіх ЕОМ розроблені стандартні програми для вирішення ЗЛП симплекс - методом.

Опишемо загальну ідею симплекса-методу.

Припустимо, що ЗЛП записано в канонічному вигляді й цільовій функції потрібно мінімізувати. Як ми вже знаємо, оптимальний план слід шукати серед опорних планів ЗЛП. Симплекс-метод не перебирає всі опорні плани (що було б часто неможливо через їхню величезну кількість), а, починаючи з деякого вихідного опорного плану, він послідовно переходить до інших опорних планів зі зменшенням цільової функції. Симплекс-метод припиняє свою роботу тоді, коли або буде знайдений оптимальний опорний план, або установлена нерозв'язність задачі.

При вирішенні ЗЛП симплекс-методом можна виділити наступні етапи:

1) приведення ЗЛП до канонічного вигляду;

2) приведення системи лінійних рівнянь до жорданової форми з невід’ємними правими частинами з одночасною перевіркою на нерозв'язність ЗЛП через суперечливість системи лінійних обмежень;

3) дослідження опорного плану на оптимальність;

4) дослідження ЗЛП на нерозв'язність через необмеженість знизу на ОПР цільової функції;

5) перехід до нового, "кращого" опорного плану.

3.2. Табличний вигляд ЗЛП. Симплекс - таблиці

Для скорочення й упорядкування записів при вирішенні ЗЛП симплекс-методом використовуються так звані симплекси-таблиці. Щоб скористатися симплекс-таблицею, ЗЛП потрібно привести до табличного вигляду. Робиться це так.

Нехай ЗЛП записана в канонічному вигляді (2.3-2.5). Для приведення ЗЛП до табличного вигляду систему (2.4) слід спочатку привести до жорданової форми з невід’ємними правими частинами. Припустимо, що ця жорданова форма має вигляд (2.6). Виразимо з (2.6) базисні змінні через вільні:

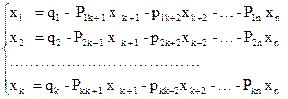(3.1)

Підставивши в цільову функцію (2.3) замість базисних змінних їхні вираження через вільні змінні за формулами (3.1), вилучимо тим самим із цільової функції базисні змінні. Цільова функція прийме вигляд:

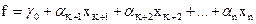(3.2)

У табличному вигляді цільова функція записується так:

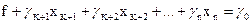(3.3)

де .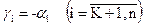

Відзначимо наступні особливості табличного вигляду ЗЛП:

а) система лінійних рівнянь приведена до жорданової форми з невід’ємними правими частинами;

б) із цільової функції виключені базисні змінні й вона записана у формі (3.3).

Перейдемо тепер до опису симплекса-таблиці. Нехай ЗЛП записана в табличному вигляді:

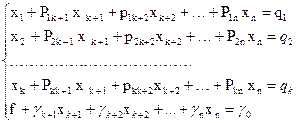(3.4)

Тоді заповнена симплекс-таблиця виглядає так.

Таблиця 3.1.

Базис	Змінні	Вільні члени
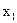
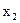
			...	xk			...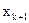
			...				...
			...				...
. . .	..	..	...	..	..	..	...	..	...
			...				...
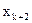
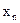
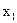
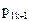
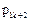
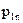
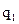
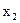
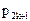
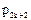
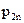
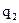
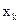
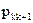
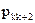
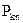
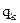
f			...				....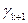

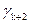
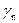
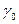
Опорний план ЗПЛ: 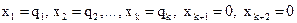..., 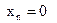називається опорним планом, що відповідає цій симплекс-таблиці. Як видно з формули (3.2), значення цільової функції при цьому опорному плані дорівнює γ_0.

Розглянемо приклад. Привести до табличного вигляду наступну ЗЛП і заповнити симплекс-таблицю:

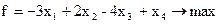
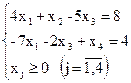
Спочатку ЗЛП потрібно привести до канонічного вигляду. Для цього функцію f потрібно замінити на - f:

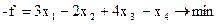
Система рівнянь повинна бути записана в жордановій формі з невід’ємними правими частинами. Загальний прийом, за допомогою якого це досягається, буде розглянутий пізніше (параграф 3.7). У нашому прикладі така жорданова форма вже є з базисними змінними 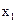і 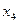. Виключимо базисні змінні із цільової функції - f. Для цього виразимо їх через вільні й підставимо ці вираження в цільову функцію.

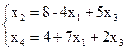
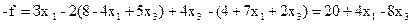
Табличний вигляд ЗЛП такий:

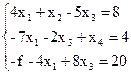
Заповнимо симплекс-таблицю (для скорочення записів перший стовпчик названий "Б", останній стовпчик - "Q").

Таблиця 3.2.

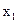
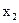
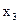
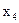
Б					Q
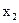
			-5
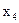
	-7		-2
-f	-4				-20

Опорний план, що відповідає цій симплекс-таблиці, має вигляд:

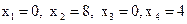. Значення функції - f при цьому опорному плані дорівнює - 20.

Дата добавления: 2014-01-07