Двоїстість у лінійному програмуванні

4.1. Економічна інтерпретація двоїстих завдань

Поняття двоїстості в лінійному програмуванні викликає великий теоретичний і практичний інтерес. Двоїста задача - це допоміжна задача лінійного програмування, що формулюється за допомогою певних правил безпосередньо з умов вихідної, або прямої задачі.

Розглянемо практичну ситуацію, що приводить до необхідності розгляду двоїстої задачі.

Підприємство випускає чотири види продукції, для виготовлення якої використовується сировина трьох видів. Запаси сировини, норми витрати сировини на одиницю продукції й прибуток від реалізації одиниці продукції наведені в наступній таблиці:

Сировина	Види продукції	Запаси сировини
П 1	П 2	П 3	П 4
Норми витрати сировини
Прибуток

Потрібно скласти такий план виробництва продукції, при якому сумарний прибуток був би найбільшим.

Для запису математичної моделі задачі позначимо через x_j кількість продукції П_j (j=1, 2, 3, 4). Математична модель задачі:

Сформулюємо тепер двоїсту задачу. Припустимо, що деяка організація вирішила купити у підприємства всю сировину. Покупець прагне установити ціни у_i на одиницю сировини i-ro виду (i = 1, 2, 3, 4) так, щоб мінімізувати сумарну вартість сировини, що виражається величиною φ=80у₁+90у₂+100у₃. При цінах, запропонованих покупцем, підприємство одержить за сировину, витрачену на виготовлення продукції П₁, виторг 2y₁+7у₂+5у₃. Підприємство погодиться на угоду з покупцем, якщо цей виторг буде не менше прибутку підприємства від виготовлення одиниці продукції П₁, тобто якщо буде виконуватися умова 2y₁+7у₂+5у₃≥14. Такого ж обмеження покупець змушений ураховувати й для всіх інших видів продукції. Таким чином, математична модель задачі, розв'язуваної покупцем, має вигляд:

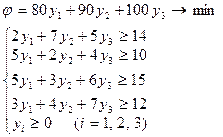
Отримана задача є двоїстою для вихідної.

З економічної точки зору зрозуміло, що f_max=φ_min. Дійсно, у випадку f_max>φ_min підприємство не буде продавати сировину, тому що при виробництві воно б одержало більший прибуток. У випадку ж f_max<φ_min покупець відмовиться від покупки сировини, тому що його плата за сировину більше прибутку від виробництва.

Результати вирішення двоїстої задачі виявляють найбільш дефіцитні види сировини (найбільш дефіцитним видом є та сировина, що в оптимальному рішенні двоїстої задачі має найбільшу ціну у_i). Аналіз рішення дозволяє визначити вплив збільшення запасів дефіцитної сировини на прибуток виробництва. Він може також підказати напрямок зміни технології виробництва, при якому дефіцитна сировина використовується в менших кількостях.

Дата добавления: 2014-01-07