Теореми двоїстості

Приведемо без доказу наступні дві теореми.

Перша теорема двоїстості. Пряма задача розв'язна тоді й тільки тоді, коли розв'язна двоїста. При цьому f_max=φ_min.

Друга теорема двоїстості. Для того, щоб два припустимих рішення x₁', x₂',...,x_n' і у₁', у₂',…,y_m' пари двоїстих задач були оптимальними, необхідно й достатньо, щоб ці рішення задовольняли умовам

Друга теорема двоїстості дає можливість знаходити оптимальне рішення однієї з пари двоїстих задач, маючи оптимальне рішення іншої задачі.

Приклад 2. Дана задача

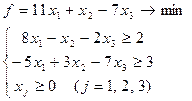
Побудувати двоїсту задачу, вирішити її геометрично, а потім за допомогою другої теореми двоїстості знайти оптимальне рішення прямої задачі.

Звернемо увагу, що дана задача записана у формі (4.4) - (4.6). Оскільки має місце принцип взаємної двоїстості, то будемо записувати двоїсту задачу у формі (4.1) - (4.3). Одержимо:

Вирішимо геометрично двоїсту задачу. Побудуємо на координатній площині граничні прямі (1) 8у₁–5у₂=11; (2) –у₁+3у₂=1; (3) –2у₁–7у₂=–7; знаходимо напівплощини, визначаємо ОПР, а потім знаходимо на ОПР оптимальну точку А (див. рисунок 4.1). Для відшукання координат точки А вирішуємо систему рівнянь

Одержуємо у₁=2, у₂=1. Підставивши ці значення змінних у цільову функцію, одержимо φ_max=7.

					Y2
									(5)
		(3)
										A
											•									(4)					Y1
						0,3			ОПР
				-1					1,4
													3,5
	(2)
							-2,2
	(1)

Рис. 4.1.

Для відшукання оптимального рішення вихідної задачі скористаємося другою теоремою двоїстості. Для цього запишемо систему рівностей (4.7) і (4.8)

Підставивши у₁=2, у₂=1, після очевидних перетворень одержимо систему

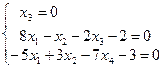
Вирішивши отриману систему, знайдемо х₁= 9/19; х₂=34/19; х₃=0; f_min= 7.

Дата добавления: 2014-01-07