Загальна постановка транспортної задачі

Задача про перевезення.

ТРАНСПОРТНА ЗАДАЧА

Симплекс-методом можна вирішити будь-яку ЗЛП. Але є такі ЗЛП, які можна вирішити простішими методами. До таких задач зараховані транспортні задачі. Прикладом транспортної задачі є задача про перевезення, задача про призначення, задача розвитку й розміщення одно- і багатопродуктових галузей.

Є m пунктів відправлення (ПВ) А₁, А₂,..., А_m, у яких зосереджений деякий вантаж у кількостях а₁,а₂,...,а_m і n пунктів призначення (ПП.) В₁, В₂,..., В_n, у які потрібно завезти цей вантаж у кількостях b₁,b₂,...,b_n, причому

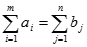. Відомі вартості c_ij перевезення одиниці

вантажу з пунктів А_i у пункти В_j (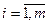; 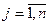). Передбачається, що

а) товар є однорідним й діленим, тобто споживачеві байдужне джерело одержуваного товару, а перевезення можуть здійснюватися партіями будь-якого розміру;

б) вартість перевезення вантажу з одного пункту в інший пропорційна кількості перевезеного вантажу.

Потрібно скласти такий план перевезень із пунктів А_i у пункти В_j, при якому витрати на перевезення були б найменшими.

Вихідні дані задачі звичайно подаються у вигляді транспортної таблиці (табл. 5.1).

Таблиця 5.1

Пп Пв	В1	В2	...	В3	Запаси
А1	с11	^С12	...	^С1n	а1
А2	^С21	^С22	...	^С2n	а2
...	...	...	...	...	...
Аm	^Сm1	^Сm2	...	^Сmn	аm
Потреби	в1	в2	...	вn

Вартості c_ij проставляються в правих верхніх кутах відповідних клітинок.

Складемо математичну модель задачі. Нехай x_ij – кількість вантажу, перевезеного з пункту А_i у пункт В_j. Цільова функція задачі (загальна вартість перевезень) записується в такий спосіб:

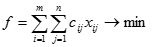
Систему обмежень записуємо, керуючись тим, що:

а) запаси пунктів відправлення повинні бути вичерпані;

б) потреби пунктів призначення повинні бути задоволені;

в) перевезення можуть бути тільки невід’ємними.

Таким чином, обмеження задачі мають вигляд:

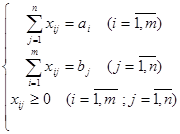
Ми бачимо, що задача про перевезення є ЗЛП.

Транспортною задачею називається ЗЛП наступного вигляду:

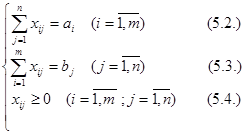
Відзначимо наступну особливість транспортної задачі як ЗЛП спеціального вигляду: система рівнянь розбита на дві групи (5.2) і (5.3) так, що кожна змінна входить рівно в одне рівняння групи з коефіцієнтом 1.

Рівняння (5.2) називаються горизонтальними, рівняння (5.3) -вертикальними.

Будь-який набір значень змінних x_ij називається планом перевезень. План перевезень називається припустимим, оптимальним або опорним, якщо він є припустимим, оптимальним або опорним планом ЗЛП (5.1 - 5.4).

Транспортна задача, як і будь-яка задача лінійного програмування, може бути вирішена симплекс-методом. Однак
завдяки зазначеній вище особливості транспортної задачі, для неї
існують більш прості методи рішення, один із яких – метод
потенціалів - ми вивчимо.

Дата добавления: 2014-01-07