Цілочислове лінійне програмування

Цілочислове програмування - розділ математичного програмування, що розглядає оптимізаційні задачі, в яких всі або деякі змінні можуть приймати тільки цілі значення. Як правило, вимога цілочисельности змінних значно ускладнює задачу. Цілочислове програмування систематично вивчається з 1956 року, але й зараз цей розділ перебуває в стадії розвитку.

6.1. Загальна постановка задачі цілочислового лінійного програмування (ЗЦЛП)

Ми будемо розглядати тільки повністю цілочислові задачі, в яких вимога цілочисельності накладена на всі змінні. Загальний вигляд такої ЗЦЛП відрізняється від ЗЛП тільки тим, що до всіх змінних ставиться вимога цілочисельности. Зокрема, у канонічному вигляді ЗЦЛП ставиться так:

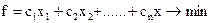(6.1)

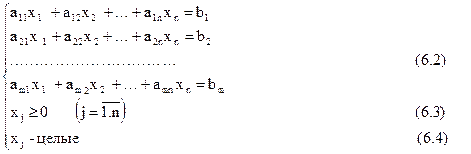
Для ЗЦЛП використовується саме така ж термінологія, що й для ЗЛП: цільова функція, припустиме рішення, оптимальне рішення тощо. Якщо в ЗЦЛП відкинути вимогу цілочисельності, то вийде так звана послаблена задача. Послаблена задача є ЗЛП, у той час як ЗЦЛП такою не є. Справа в тому, що вимога цілочисельності змінних не можна записати у вигляді лінійного обмеження. Аналітично його записати можна. Дійсно, позначимо через [a] цілу частину числа а, тобто найбільше ціле, що не більше а. Наприклад, [3.4] =3; [-7.2]= -8. Вимога цілочисельності змінної x_j можна записати так: x_j -[x_j ] =0. Однак це співвідношення не є лінійним. Таким чином, не можна сказати, що ЗЦЛП є окремий випадок ЗЛП - вона взагалі не є ЗЛП.

Для ЗЦЛП не існує такого універсального ефективного методу вирішення, яким є симплекс-метод для ЗЛП. З точних методів вирішення відзначимо метод відсікання Гоморі й комбінований метод гілок та меж. Суть цього комбінованого методу ми викладемо.

На практиці більшість ЗЦЛП вирішується приблизно. При цьому часто доводиться розробляти наближений метод, що враховує специфічні особливості задачі.

Наведемо приклади ЗЦЛП.

6.2. Цілочислова задача про використання сировини

Підприємство випускає n видів штучної продукції вартістю 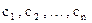за штуку. Для виготовлення продукції використовується m видів сировини, запаси якої на підприємстві рівні відповідно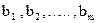. Відома (m х n) – матриця (a_ij), в якій 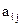- витрата i – ої сировини на виробництво одиниці продукції j -го виду. Потрібно скласти такий план виробництва, при якому прибуток від реалізації продукції був б найбільшим.

Математична модель задачі має вигляд:

f =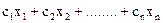→ max

при обмеженнях:

Тут 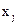- кількість продукції j -го виду.

Це задача цілочислового лінійного програмування.

Цілочисельність змінних суттєва в тих випадках, коли мова йде про виробництво цінної продукції.

Дата добавления: 2014-01-07