Вирішення ЗЦЛП методом округлення

Задача про рюкзак

Цілочисельність задачі про використання сировини не є яскраво вираженою ЗЦЛП. До типових ЗЦЛП зараховані так звані комбінаторні оптимізаційні задачі. У комбінаторних задачах є кінцева множина варіантів, з яких потрібно вибрати оптимальний. Прикладом такого задачі є задача про рюкзак.

Є рюкзак місткістю V і n предметів об’ємами v₁, v₂,...,v_n і вартостями с₁, c₂ ,..., c _n. Потрібно впакувати рюкзак так, щоб вартість упакованих предметів була максимальною.

Складемо математичну модель цієї задачі.

Нехай x_j – змінна, що приймає тільки два значення: 0 або 1, причому x_j =0, якщо j- й предмет не впаковується в рюкзак; x_j = 1, якщо j- й предмет упаковується в рюкзак. Тоді задача записується так:

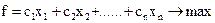
при обмеженнях

Ця ЗЦЛП називається задачею булєва програмування. Обмеження задачі можна записати інакше:

Метод округлення - найпростіший метод наближеного вирішення ЗЦЛП. Його сутність полягає в тому, що вирішується ослаблена задача (як задача лінійного програмування) і отримане оптимальне рішення ЗЛП округляється до цілочислового рішення. Цей метод має два суттєвих недоліки:

1) у результаті округлення може вийти неприпустиме рішення;

2) рішення, отримане в результаті округлення, будучи припустимим, може значно відрізнятися від оптимального.

Приклад 1.

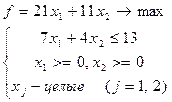
Вирішивши геометрично ослаблену задачу, одержуємо оптимальне рішення:

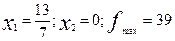
Зробимо округлення:

1) x₁=2; x₂=0. Одержимо неприпустиме рішення - не задовольняється обмеження 7x₁+4x₂<=13 (дійсно, 7*2+4*0<=13 – хибна нерівність).

2)х₁=1; х₂=0. Це припустиме рішення. Значення цільової функції f=21*1+11*0=21, що значно відрізняється від оптимального значення.

Оптимальне рішення цієї ЗЦЛП таке: х₁=0; х₂=3; f_max =33.

Метод округлення можна використовувати тоді, коли цільова функція малочутлива до змін змінних у межах одиниці.

Дата добавления: 2014-01-07