Метод аналізу ієрархій

У процесі розв’язання складних проблем застосовуються систематичні процедури, однією із котрих є метод аналізу ієрархій (Analytic Hierarchy Process), опрацьований американським системним аналітиком Томасом Л. Сааті (Thomas L. Saaty) по його відомих результатах у сфері „неструктурованого прийняття рішень” (Non-structured Decision Making). Загальним для цих процедур є використання декомпозиції для зменшення числа можливих помилок у процесі опрацювання експертних висновків. Застосування методу аналізу ієрархій приводить до структури у вигляді мультидерева, дозволяє уникнути складних порівнянь, замінивши їх попарними, та, окрім того, володіє засобами перевірки несуперечності висновків експерта. Цим пояснюється широка розповсюдженість методу, його дійсно системний характер та велика кількість практичних застосувань. При залученні кваліфікованих експертів та досвідченого системного аналітика цей метод дозволяє генерувати рішення, що відповідають меті складної системи. Отже:

метод аналізу ієрархій – це систематична процедура, що основна на ієрархічному представленні елементів, які визначають суть проблеми, що розбивається на простіші складові із наступною оцінкою особою, яка приймає рішення, ступеня взаємодії елементів отримуваної ієрархічної структури. У методі використовуються жорсткі оцінки у шкалі відношень. Він побудований на принципі ідентичності та декомпозиції і включає процедури синтезу множинних тверджень та знаходження альтернативних рішень.

Існує ряд модифікацій методу, що визначаються характером зв’язків між критеріями та альтернативами, розташованими на найнижчому рівні ієрархії, а також способом порівняння альтернатив: попарним порівнянням; порівнянням альтернатив щодо стандартів та порівняння альтернатив копіюванням.

Проблема, що її треба вирішити, зводиться до обґрунтованого вибору альтернативи із числа можливих, які характеризуються складною ієрархією аспектів та критеріїв.

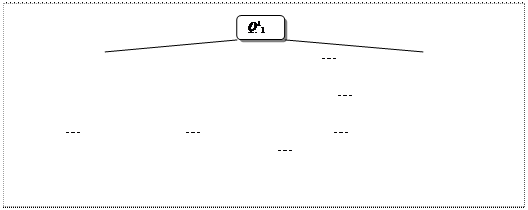
Побудова ієрархії починається із окреслення досліджуваної проблеми. Далі будується власне ієрархія, що включає мету системи, якій відповідає корінь ієрархії, проміжні рівні (аспекти мети, мета-критерії, критерії) та альтернативи, що формують найнижчий ієрархічний рівень (листя). Загальний вигляд ієрархії, де Q – елементи ієрархії, В – альтернативи, представлений наступним Рис. 25.

Рис. 25. Загальний вигляд ієрархії в методі аналізу ієрархій

Верхній індекс у елементів вказує рівень ієрархії, а нижній – їхній порядковий номер. Елементи порівнюються попарно стосовно їх дії (ваги, інтенсивності) на спільну характеристику. Якщо В = { B ₁,…, B _n } – множина елементів, а W = { w ₁,…, w _n} – відповідно їх ваги, або інтенсивності, то елементи матриці їх порівняльної важливості A = { a _ij} визначаються за формулою a _ij = w _i/ w _j. Якщо W невідомий, то попарні порівняння реалізуються на основі суб’єктивних тверджень, оцінюваних за певною шкалою, й за цими даними знаходяться.

В ієрархії виділяють елементи двох типів: елементи – предки та елементи – нащадки. Парні порівняння реалізуються у термінах домінування. Отримані твердження виражаються у цілих числах дев’ятибальної шкали. Значення елементів матриць визначаються у результаті опитування експертів.

Як результат після порівнянь для множини нащадків кожного предка отримують позитивно обернену симетричну матрицю.

Для реалізації суб’єктивних парних порівнянь використовують дев’ятибальну шкалу:

Таблиця 10.3. Шкала відносної важливості методу аналізу ієрархій

Бал k	Визначення	Примітка
	Рівна важливість	Рівний вклад двох видів діяльності в мету
	Помірна перевага	Легка перевага одного виду діяльності над іншим
	Суттєва перевага	Відчутна перевага одного виду діяльності над іншим
	Значна перевага	Практично значна перевага одного виду діяльності над іншим
	Дуже велика перевага	Очевидна перевага – домінування одного виду діяльності над іншим
2,4,6,8	Проміжні значення	Застосовується у перехідних випадках
1/ k	Обернені величини	Використовується для оцінки не переважаючих видів діяльності

Заповнення квадратної матриці А попарних порівнянь відбувається наступним чином.

А = = .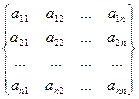

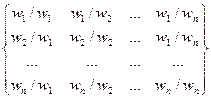Матриця будується для кожного елемента-предка, її розмір n n визначається кількістю безпосередніх нащадків n у цього елемента-предка. Якщо елемент – нащадок В _i домінує, тобто він кращий елемента – нащадка предка В _j, то експерт визначає ступінь домінування, використовуючи наведену вище шкалу в термінах визначень, і відповідне значення в балах присвоюється елементу а _ij, а значення 1/ а _ij – елементу а_ji (оскільки природно, що якщо В_i є кращий, ніж В_j у а _ij разів, то В_j „кращий” за В_i у 1/ а _ij разів, або, що еквівалентно, В_j гірший за В_i у а _ij разів). Отже, матриця А є обернено симетричною, тобто для всіх її елементів а _ij = 1/ а _ji, а елементи головної діагоналі дорівнюють 1.

У процесі реалізації попарних порівнянь формулюють наступні запитання:

· Який з двох варіантів важливіший чи більше впливає?

· Який з двох варіантів імовірніший?

· Який з двох варіантів має більшу перевагу?

Для більшості застосувань запитання потрапляє, зазвичай, в одну із цих категорій. При порівнянні критеріїв питають, який із критеріїв важливіший; при порівнянні альтернатив за критеріями – яка із альтернатив є бажанішою; при порівнянні сценаріїв, котрі отримують із критеріїв, - який є більш імовірний.

У випадках, коли важко розрізнити стільки проміжних градацій, може використовуватися шкала із меншим числом градацій. Гранично може бути дві градації: 1 – об’єкти рівнозначні; 2 – перевага одного над другим.

Локальним завданням є визначення „ваг” W = { w ₁, w ₂, …, w _n} кожного із нащадків відносно усіх вершин ієрархії (за винятком листя) і хочеться, щоби відповідальна особа або експерт вказали ці ваги. Однак, практично безпосереднє призначення здійсненне лише для випадку, коли є два елементи. Якщо ж елементів-нащадків більше трьох, виникають суттєві складності – оскільки у цьому випадку висновки експерта будуть суперечливими та ненадійними, що підтверджено багатьма дослідженнями. У цьому „винні” психологічні особливості людини-експерта, для якої значно простіше виконати ряд попарних порівнянь нащадків між собою, аніж відразу присвоїти їм певні ваги, що відображають вклад деякого елемента-нащадка в елемент-предок. Саме цим пояснюється необхідність методу попарних порівнянь, бо ця інформація надалі використовується для отримання значень ваг та оцінювання послідовності висновків експерта.

На цьому кроці формуються локальні пріоритети на основі матриць попарних порівнянь. Змістовно це є знаходження бажаності, сили впливу, цінності чи імовірності кожного окремого об’єкта-нащадка відносно безпосереднього об’єкта-предка.

Локальні пріоритети отримують шляхом обчислення головних власних векторів для кожної з обернено симетричних матриць ієрархії та нормалізації результату.

Обчислення головного власного вектора x = { x ₁, x ₂,…, x _n} позитивної квадратної матриці А = { a _ij) реалізується шляхом визначення рівності Аx =λ _max, де λ _max – максимальне власне значення матриці А.

Для позитивної квадратної матриці А правий власний вектор x, що відповідає максимальному власному значенню λ _max, можна обчислити із точністю до постійного співмножника за наступною формулою:

= Cx,

де е = {1,1,…,1}^т - одиничний вектор, k = 1,2,... – показник степеня, C - константа, T - знак транспонування.

Обчислення власного вектора відбувається до досягнення заданої точності за співвідношенням е ^т| x ^(k) – x ^(k-1)| ≤ ε, де k – номер ітерації, ε - точність обчислень.

Практично можна вважати, що ε =.01, незалежно від порядку матриці А.

Максимальне власне значення обчислюється за формулою λ _max = е ^т Ах. Для цього можна скористатися програмним пакетом Mathcad, або наближено отримати шляхом обчислення середнього геометричного рядків матриці попарних порівнянь А = { a _ij) із наступною нормалізацією компонент отриманого вектора за формулою:

x _i = /.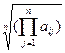

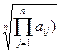Значення вектора x = { x ₁, x ₂,…, x _n} використовуються в подальших обчисленнях.

Оскільки експерт оцінює переваги шляхом попарних порівнянь, рівність a _ij a _jk = a _ik, що мала б виконуватися для всіх i, j та k, буде порушуватися. Чим більше порушень цих рівностей, тим менше можна довіряти результатам опитування експертів і це свідчитиме про суперечливість висновків експерта або про його некомпетентність в даній предметній області. Для оцінки однорідності тверджень експерта використовується відхилення величини максимального власного значення λ _max від порядку матриці А.

Отримана у результаті опитування експерта матриця буде неузгодженою, тобто свідчитиме про певну непослідовність висновків експерта, що у реальних умовах завжди існує. Оцінити неузгодженості можна за допомогою індексу узгодженості за формулою:

I и= = , звідси λ _max =

Індекс I и порівнюють із значенням, що отримують за умови вибору значень із шкали 9, 8, 7,..., 1/8, 1/9 зі збереженням умови оберненої симетричності випадкової матриці. Середні значення для випадкових матриць різного розміру наведені нижче.

Розмір матриці
Випадкова узгодженість			.58	.9	1.12	1.24	1.32	1.41	1.45	1.49	1.51	1.53	1.56	1.57	1.59

Відношення узгодженості є часткою від ділення індексу узгодженості на відповідне значення випадкової узгодженості: I ₀ = I и/ М ( I и).

Якщо отримане значення менше 10%, то рівень узгодженості можна вважати задовільним, а у деяких випадках можна обмежитися 20%.

При практичному застосуванню методу аналізу ієрархій слід мати на увазі, що для обґрунтованих числових порівнянь оптимальною кількістю є число 7 (2).

Перевагами методу є його вклад в аналіз структури проблеми та чітке висловлювання тверджень. Загальна мета (фокус) проблеми відповідає вищому рівню ієрархії. Наступний рівень – найважливіших критеріїв, далі – підкритеріїв, та, нарешті, рівень альтернатив.

Отже, основним завданням методу аналізу ієрархій є розрахунок глобальних пріоритетів альтернатив відносно усієї ієрархії.

З’ясуємо окремі положення методу, розглянувши наступні приклади.

Приклад 1.

Задано: Для порівняльного оцінювання чотирьох моделей комп’ютерів А, Б, В та Г експерт виконав попарні порівняння та дав наступні оцінки:

1. Модель В помітно переважає модель А.

2. Модель Б помітно поступається моделі В.

3. Модель А значно переважає модель Г.

4. Перевага моделі В над Г знаходиться між значною та дуже великою.

5. Модель А помітно поступається моделі Г.

6. Модель Б помітно переважає модель Г.

Шукане: матриця попарних порівнянь.

Розв’язок: Перевіряється, чи можна на основі цих тверджень отримати повну матрицю попарних порівнянь. Серед тверджень відсутні симетричні. Нагадаємо, що якщо такі зустрічаються, то вони вважаються як одне, а оцінка обчислюється як середнє геометричне прямої та оберненої до оберненої оцінок.

Будується матриця, рядки та стовпчики якої відповідають моделям А, Б, В та Г. Оскільки об’єкт порівняння є рівно важливим сам до себе, то ясно, що на головній діагоналі будуть 1. Далі матриця заповнюється парами елементів, симетричними відносно головної діагоналі, що відображають кожне твердження експерта.

Шляхом перегляду тверджень експерта будується матриця А попарних порівнянь:

А = .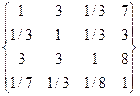

Приклад 2.

Задано: Родина бажає придбати автомобіль. Аналіз виявив наступні критерії, що треба врахувати: престижність, вартість, витрати пального, комфортність, надійність, максимальна швидкість, розміри, технічне обслуговування, гарантії.

Шукане: побудувати матрицю ієрархії методу аналізу ієрархій.

Розв’язок: В якості кандидатів вибрали три моделі та задачу представили у вигляді ієрархії (Рис. 26)

Рис. 26. Декомпозиція задачі купівлі автомобіля

Після аналізу первинна множина критеріїв була звужена до наступних суттєвих: Q₁ - комфортабельність; Q₂ - надійність; Q₃ - швидкість; Q₄ - вартість; Q ₅ - престижність; Q₆ - обслуговування; Q₇ - гарантії; Q₈ - витрати пального.

Шляхом опитування членів родини побудували наступну матрицю попарних порівнянь для рівня 2 – критеріїв.(Рис. 27)

	Q1	Q2	Q3	Q4	Q5	Q6	Q7	Q8
Q1	1	5	3	7	6	6	1/3	1/4
Q2	1/5	1	1/3	5	3	3	1/5	1/7
Q3	1/3	3	1	6	3	4	6	1/5
Q4	1/7	1/5	1/6	1	1/3	1/4	1/7	1/8
Q5	1/6	1/5	1/3	3	1	1/2	1/5	1/6
Q6	1/6	1/3	¼	4	2	1	1/5	1/6
Q7	3	5	1/6	7	5	5	1	1/2
Q8	4	7	5	8	6	6	2	1

Рис. 27. Матриця попарних порівнянь критеріїв Q₁ – Q₂ купівлі автомобілів

Після цього, порівнюючи попарно три автомобіля А, В та С за кожним із критеріїв (рівень 3), отримали вісім матриць (для кожного із критеріїв) розміром 33 (за кількістю альтернатив) (Рис. 28).

	1	Q2	Q3	Q4	Q5	Q6	Q7	Q8	Вектор пріоритетів
Q1	1	5	3	7	6	6	1/3	1/4	.173
Q2	1/5	1	1/3	5	3	3	1/5	1/7	.054
Q3	1/3	3	1	6	3	4	6	1/5	.188
Q4	1/7	1/5	1/6	1	1/3	1/4	1/7	1/8	.018
Q5	1/6	1/5	1/3	3	1	1/2	1/5	1/6	.031
Q6	1/6	1/3	¼	4	2	1	1/5	1/6	.036
Q7	3	5	1/6	7	5	5	1	1/2	.167
Q8	4	7	5	8	6	6	2	1	.333

Q1	А	В	С	Q2	А	В	С	Q3	А	В	С	Q4	А	В	С
А	1	6	8	А	1	7	1/5	А	1	1	6	А	1	1	1
В	1/6	1	4	В	1/7	1	1/8	В	1/8	1	1/4	В	1	1	1
С	1/8	1/4	1	С	5	8	1	С	1/6	4	1	С	1	1	1
Q5	А	В	С	Q6	А	В	С	Q7	А	В	С	Q8	А	В	С
А	1	5	4	А	1	8	6	А	1	1/2	½	А	1	1/7	1/5
В	1/5	1	1/3	В	1/8	1	1/5	В	2	1	1	В		1	3
С	1/4	3	1	С	1/6	5	1	С	2	1	1	С	5	1/3	1

Рис. 28. Матриці попарних порівнянь альтернатив А, В та С за критеріями

Приклад 3.

Задано: матриця попарних порівнянь критеріїв (Рис.27) та матриці попарних порівнянь альтернатив А, В та С за критеріями (Рис. 28)

Шукане: оцінити послідовності тверджень експерта та розрахувати локальні пріоритети ієрархії.

Розв’язок: результати розрахунку вектора пріоритетів, індексу узгодженості для матриці попарних порівнянь критеріїв представлені на Рис. 29.

I и.0238

I ₀.169

Рис. 29. Розрахунок узгодженості матриці критеріїв

Вектор пріоритетів отриманий у результаті розрахунку головного власного вектора із наступною його нормалізацією.

Щодо інтерпретації результатів, то у цьому випадку витрати пального є найважливішим критерієм при виборі автомобіля, друге місце за комфортністю, а третє – за швидкістю руху.

Розраховані відповідні характеристики для множини таблиць наступного рівня – оцінювані альтернати представлені на Рис. 30.

Q1	A	B	C		Q2	A	B	C
A	1	6	8	.754	A	1	7	1/5	.674
B	1/6	1	4	.181	B	1/7	1	1/8	.101
C	1/8	1	4	.065	C	5	8	1/8	.226
			Iu=	.068				Iu=	.043
			I0=	.117				I0=	.074
Q5					Q8
A	1	5	4	.745	A	1	8	6	.200
B	1/5	1	1/3	.065	B	1/8	1	1/5	.400
C	1/4	3	1	.181	C	1/6	5	1	.400
			Iu=	.068				Iu=	.000
			I0=	.117				I0=	.000
Q3					Q4
A	1	8	6	.233	A	1	1	1	.747
B	1/8	1	1/4	.005	B	1	1	1	.060
C	1/6	4	1	.713	C	1	1	1	.193
			Iu=	.124				Iu=	.099
			I0=	.213				I0=	.170
Q7					Q8
A	1	1/2	1/2	.333	A	1	1/7	1/5	.072
B	2	1	1	.333	B	7	1	3	.650
C	2	1	1	.333	C	5	1/3	1	.278
			Iu=	.000				Iu=	.032
			I0=	.000				I0=	.056

Рис. 30. Розраховані значення локальних пріоритетів для альтернатив за кожним із критеріїв Q_{1 –} Q₈

Приклад 4.

Дано: результати прикладів 2 та 3, що розглянуті вище.

Шукане: глобальні пріоритети альтернатив.

Розв’язок: розрахунок глобальних пріоритетів здійснюється на етапі ієрархічного синтезу. Для виявлення глобальних пріоритетів автомобілів виконується обернений хід – із передостаннього рівня рухаються до кореня ієрархії, збираючи вектори локальних пріоритетів у матриці та множачи їх на вектори локальних пріоритетів безпосередніх предків до моменту досягнення кореня ієрархії.

Ця процедура зводиться до збирання матриці з векторів локальних пріоритетів альтернатив за критеріями s = 2.

P ₁⁽¹⁾ =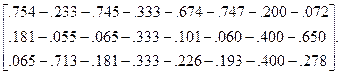

Вектор локальних пріоритетів відносно кореня дерева χ ₁⁽¹⁾ =[.173.054.188.018.031.167.333]^T, де Т – знак транспозиції, вжитий для зображення вектора - стовпця рядком.

P ₁⁽¹⁾ = P ₁⁽¹⁾ χ ₁⁽¹⁾ = .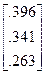

Оскільки оновлене значення і = 0, то робота алгоритму закінчена.

Отже, за загальним показником (не дивлячись на найгірші показники за найважливішим критерієм – витрати пального) обирається автомобіль А, тому що інші аспекти є у нього на дуже непоганому рівні порівняно із В та С.

Приклад 5.

Дано: зображена на Рис. 31 ієрархія проблеми – ієрархія критеріїв та альтернатив та для кожного елементу визначений індекс однорідності I и(Q_j) і вектори пріоритетів критеріїв відносно критеріїв-предків x _j, де j – індекс предка. Також розраховані індекси однорідності: I и(Q₁) - для першого рівня; I и(Q₂) та I и(Q₃) - для другого рівня; I и(Q₄), I и(Q₅) та I и(Q₆) - для третього рівня, а також x ₁ - вектор пріоритетів критеріїв Q₂, та Q₃ відносно критерію-предка першого рівня ієрархії Q₁; x _2, та x ₃ - вектори пріоритетів критеріїв Q₄, Q₅, Q₆ відносно критеріїв-предків другого рівня Q₂, та Q_3..

...

Рис. 31. Структура ієрархії проблеми

Шукане: індекс узгодженості та відношення узгодженості для ієрархії.

Розв’язок: Індекс однорідності даної ієрархії визначається за наступною формулою:

I и = I и(Q₁) + р₁^Т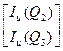+ p₁^T (p ₂ p ₃)^T,

де Т – знак транспонування.

Визначення відношення однорідності для усієї ієрархії здійснюється за формулою І ₀ = I и/ М (I и), де М (I и) – індекс однорідності ієрархії при випадковому заповненні матриць попарних порівнянь.

Розрахунок індексу однорідності ієрархії М (I и) при випадковому заповненні матриць попарних порівнянь виконується за формулою, що аналогічна формулі визначення індексу однорідності:

М (I и) = М (I и(Q₁)) + р₁^Т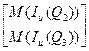+ p₁^T (p ₂ p ₃)^T.

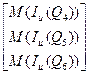Однорідність ієрархії вважається задовільною при значеннях І ₀, що не перевершують.1, а в окремих випадках.2.

Дата добавления: 2014-01-07