
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод комбінаторно-морфологічного аналізу та синтезу
|
|
|
|
Метод комбінаторно - морфологічного аналізу та синтезу був запропонований у 1969 р. швейцарським математиком та астрономом Фрицем Звіки (Fritz Zwicky) для вивчення нових геометричних форм створюваних технологічних систем.
Основна ідея комбінаторно-морфологічного підходу полягає ув тому, щоб знаходити найбільшу кількість, а гранично й усі можливі розв’язки проблеми шляхом комбінування основних структурних елементів системи або ознак рішень.
Морфологія – це структурна форма системи, що організована відповідно до її функцій.
Термін „морфологічний аналіз” дуже старий і йде від філософа та теолога Раймунда Лулія (латиниз., Lullius), ким була висунута ідея логічної машини, викладена у творі „Велике мистецтво”, відповідно до якої шляхом систематичної комбінації невеликого числа принципів виникає можливість розв’язати усі проблеми філософії та метафізики. Французький філософ, математик, фізик та фізіолог Рене Декарт (1596 – 1650) побачив у цьому небезпеку механізації мислення, бо вважав, що силогізми в логіці допомагають пояснити лише те, що вже відомо, і безглуздо міркувати про те, чого не знають, замість того, щоб це вивчити.
Німецький філософ, математик, фізик та мовознавець Готфрід Вільгельм Лейбніц (Leibniz) (1646 – 1716) навпаки, був послідовником Лулія і говорив про нього із гордістю у своїй дисертації „Про мистецтво комбінаторики” (1666), де дав узагальнення комбінаторного методу. Привід для негативної оцінки методу Лулія дали його послідовники в ХVІІ та ХVІІІ ст. Так, автор „Мандрів Гулівера” Джонатан Свіфт (1667 – 1745) із гумором описав механічний пристрій, що випадковим чином комбінував букви й у такий спосіб „дозволив най неосвіченим людям писати книги без усякої допомоги таланту або науки”. Проте критика Свіфта допомогла визначити, чим є комбінаторно-морфологічний аналіз, що фактично ж є методом розвитку творчих здібностей, або, точніше, систематичним допоміжним засобом для творчості. Він стимулює творчу працю та розширює її можливості, поширюючи на більше число ідей, ніж це було б можливим при класичному підході.
Основні принципи морфологічного дослідження наступні:
· рівний інтерес до усіх об’єктів морфологічного дослідження;
· ліквідація усіх обмежень та оцінок до моменту одержання повної структури досліджуваної області;
· максимально точне формулювання поставленої проблеми.
Однією із складових методу комбінаторно-морфологічного аналізу є метод систематичного покриття поля. Вважається, що існує деяка кількість так званих „“опорних пунктів” знання в довільній області, що досліджується. Цими пунктами можуть бути теоретичні положення, емпіричні факти або відкриті закони, у відповідності до котрих виконуються різні процеси тощо. Виходячи з обмеженої кількості опорних пунктів знання та достатньої кількості принципів мислення, за допомогою морфологічного методу покриття поля шукаються всі розв’язки існуючої проблеми.
Ще однією із складових методу комбінаторно-морфологічного аналізу є метод заперечення та конструювання, що використовується наступним чином:
· формується множина висловлювань (положень, тверджень, аксіом), що відповідають сучасному рівню розвитку досліджуваної області знання;
· замінюється одне, декілька або усі твердження на протилежні;
· будуються можливі наслідки, що витікають із такого заперечення;
· перевіряється несуперечність отриманих висловлювань та тих, що залишилися.
Метод комбінаторно-морфологічного аналізу та синтезу включає наступні кроки:
· формування первинної мети або проблеми, що відображає основні вимоги до об’єкта, який синтезують;
· побудова морфологічної таблиці;
· опис властивостей альтернатив морфологічної таблиці. Ці властивості можуть бути висловлені в якісній шкалі найменувань класифікаційними, функціональними та структурними ознаками або в числовій шкалі, що відображає якість альтернатив за різними критеріями;
· формування функції мети та пошукового завдання у формалізованому вигляді;
· пошук варіантів розв’язку завдання як послідовності операцій вибору із морфологічної множини варіантів описання функціонування системи і операцій оцінювання ефективності та сумісності підсистем, що повинні утворювати цілісний варіант з наступним визначенням відповідності вимогам до остаточної функціональної системи (припустиме, непогане, якісне чи дуже гарне рішення).
Метод комбінаторно-морфологічного дослідження реалізується у два етапи.
1. Одержання описів всіх систем, що належать до досліджуваного класу, тобто класифікація множини систем.
2. Оцінка описів різних систем досліджуваного класу та вибір тих, що у тому чи іншому наближенні відповідають умові задачі. Цей етап називається морфологічним синтезом, тому що в результаті отримують цілісний опис усієї системи на рівні описів окремих підсистем та відношень між ними.
Цілями комбінаторно-морфологічного аналізу та синтезу систем є наступне:
Системне дослідження усіх можливих варіантів розв’язків задачі, що випливають із закономірностей побудови (морфології) об’єкта та не дозволяють врахувати, крім відомих, незвичайні варіанти, що могли б бути опущені аналітиком.
Пошук на морфологічній множині варіантів описів функціональних систем, що відповідають умові задачі.
Формулювання первісної мети синтезу здійснюється із різним ступенем повноти та визначеності. Якщо перед системним дослідником поставлена задача опрацювання нової соціально-економічної системи, то початкова мета буде досить загальною, розпливчатою, наприклад: „Створити ефективну інформаційну систему установи”; „Покращити систему перевезень у межах міста”; „Спроектувати ефективну систему роботи супермаркету” тощо.
Якщо процес синтезу пов’язаний із удосконаленням соціально-економічних систем, то первісна мета конкретизується економічними, соціальними та технологічними вимогами, якісними чи кількісними. Цей спосіб формулювання мети синтезу краще формалізується, і на його базі реалізований ряд підходів із синтезу раціональних варіантів систем.
Існують наступні три основні підходи до формулювання пошукових завдань.
Стосовно першого підходу пошукове завдання формулюється на основі якісних класифікаційних ознак, що характеризують окремі підсистеми варіанта системи. При другому пошукове завдання формулюється на основі кількісної експертної шкали критеріїв якості та необхідного рівня їхнього досягнення. Третій підхід орієнований на вибір раціонального варіанта із морфологічної множини без безпосереднього виділення пошукового завдання. Тобто використовується лише інформація, що характеризує властивості та якість альтернатив із морфологічної таблиці.
Формування пошукового завдання на основі множини класифікаційних якісних ознак значно ефективніше, якщо функціонують бази даних, де накопичуються найважливіші класифікації різних економічних, менеджерських або організаційних систем.
Формування пошукового завдання на базі кількісних ознак має ряд особливостей. Пошукові образи альтернатив, що реалізують функції системи, є числовими характеристиками, що відображають ступінь прояву різних властивостей, таких як надійність підсистем, їх технологічність, вартість тощо.
Визначення числових значень критеріїв, що характеризують з одного боку пошукове завдання, а з іншого – альтернативи із морфологічної таблиці, реалізуються двома методами: порівняння із еталоном та попарного порівняння. Практично в якості еталона може використовуватися існуюча чи гіпотетична альтернатива, властивість якої за певним критерієм оцінюється максимальним значенням обраної числової шкали.
Пошукове завдання складається наступним чином: 1) формується безпосередньо на морфологічній таблиці у вигляді комбінацій альтернатив по одній із кожного рядка (кожен рядок таблиці відповідає певній функції системи, а елемент рядка – варіанту реалізації цієї функції – альтернативі). Одержання значень показників якості для функціональних альтернатив при попарному порівнянні основане на розрахунку власного вектора матриці попарних порівнянь. Матриці попарних порівнянь будуються для альтернатив певної функціональної підсистеми, що входить у морфологічну таблицю; 2) формується у вигляді деякого гіпотетичного ідеального варіанта, елементи якого, що відповідають кожному рядку морфологічної таблиці, мають за всіма критеріями якості найкращі граничні властивості. Останні визначаються експертами. При методі попарних порівнянь щодо еталонів гіпотетичні альтернативи, що утворюють пошукове завдання, оцінюються за критеріями якості найвищою оцінкою.
Пошукове завдання може формуватися на підставі бажаного для експерта ступеня якості синтезованих варіантів систем.
Морфологічна таблиця матиме наступний вигляд (табл.10.4.)
Таблиця 10.4. Способи формування пошукових завдань
| F | A | Pr | Pj | Pg | ||
| F1 A(1) Q1(1) Q2(1) … Qu1 (1) | a1(1) a1(1) | … | ak1(1) | a1(1) | ||
| q11(1) q12(1) | … | q1k1(1) | 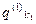
| 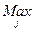 q1j(1) q1j(1)
| qe1(1) | |
| q21(1) q22(1) | … | q2k1(1) | 
| 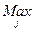 q2j(1) q2j(1)
| qe2(1) | |
| … … | … | … | … | … | … | |
| qug1(1) qug2(1) | … | qu1k1(1) | 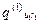
| 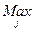 q q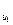 j(1) j(1)
| 
| |
| F2 A(2) Q1(2) Q2(2) … Qu2(2) | a1(2) a2(2) | … | ak2(2) | ak2(1) | ||
| q11(2) q12(2) | … | q1k2(2) | 
| 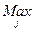 q1j(2) q1j(2)
| qe1(2) | |
| q21(2) q22(2) | … | q2kg(2) | 
| 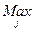 q2j(2) q2j(2)
| qe2(2) | |
| … … | … | … | … | … | … | |
| qug1(2) qug2(2) | … | qu2k2(2) | 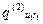
| 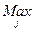 q q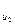 j(2) j(2)
| 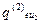
| |
| … … | … … | … | … | |||
| Fg A(g) Q1(g) Q2(g) … Qug(g) | a1(g) a2(g) | … | akg(g) | ar (g) (g)
| ||
| q11(g) q12(g) | … | q1kg(g) | 
| 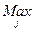 q1j(g) q1j(g)
| 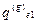
| |
| q21(g) q22(g) | … | q2kg(g) | 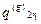
| 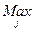 q2j(g) q2j(g)
| 
| |
| … … | … | … | … | … | … | |
| qug1(g) qug2(g) | … | qugkg(g) | 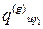
| 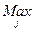 q q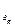 j(g) j(g)
| 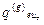
|
У цій таблиці реалізація кожної і -ї функції системи F i можлива одним із елементів відповідної множини варіантів A (i ) = { a 1(i), a 2(i),…, a r (i) }. Якість реалізації функції F i оцінюється за множиною критеріїв Q (i) = { Q 1(i), Q 2(i),…, Q u
(i) }. Якість реалізації функції F i оцінюється за множиною критеріїв Q (i) = { Q 1(i), Q 2(i),…, Q u (i) }, так що q kd(i ) є значенням якості варіанта реалізації функції F i за критерієм Q k(i). Якщо пошукове завдання формується 1-м способом (стовпчик таблиці, що відповідає пошуковому завданню P r), то у випадку виконання умов цілісності воно й буде розв’язком; у випадку пошукового завдання у вигляді ідеального (стовпчик P i) немає обраних варіантів реалізації функцій, але з кожного рядка таблиці обране найкраще значення, і реально обраною в результаті дослідження повинна бути така комбінація реалізацій функцій, що не порушує цілісність системи і є найближчою до ідеальної. І, нарешті, при третьому способі експерти визначають еталонні значення критеріїв якості реалізації функцій, шукаючи найближчі до еталонного розв’язки.
(i) }, так що q kd(i ) є значенням якості варіанта реалізації функції F i за критерієм Q k(i). Якщо пошукове завдання формується 1-м способом (стовпчик таблиці, що відповідає пошуковому завданню P r), то у випадку виконання умов цілісності воно й буде розв’язком; у випадку пошукового завдання у вигляді ідеального (стовпчик P i) немає обраних варіантів реалізації функцій, але з кожного рядка таблиці обране найкраще значення, і реально обраною в результаті дослідження повинна бути така комбінація реалізацій функцій, що не порушує цілісність системи і є найближчою до ідеальної. І, нарешті, при третьому способі експерти визначають еталонні значення критеріїв якості реалізації функцій, шукаючи найближчі до еталонного розв’язки.
Морфологічні таблиці дозволяють систематизувати великий обсяг знань про морфологію системи у конкретному вигляді. Опрацювання морфологічної таблиці дає можливість формалізувати процес упорядкування множини варіантів системи. Якість складання морфологічної таблиці визначає остаточний результат пошуку розв’язку проблеми. Це перший етап морфологічного дослідження – морфологічний аналіз, метою якого є класифікація досліджуваних об’єктів.
Формування конкретних морфологічних таблиць для відображення множини систем реалізується двома способами, вибір котрих визначається метою морфологічного дослідження, характером інформації та ступенем вивченості предметної області.
Перший спосіб основується на функціонально-елементному аналізі систем. У результаті формується морфологічна таблиця, що включає функції або узагальнені функціональні підсистеми та альтернативи, котрі реалізують відповідні функції (див. таблицю вище). Альтернативи оцінюються експертами кількісно за критеріями якості.
При опрацюванні морфологічних таблиць класифікаційні ознаки повинні дати можливість кількісної оцінки. Такими основними характеристиками складних систем є функції та елементи, що їх реалізують. Спершу будується дерево функцій системи (аналогічно до дерева цілей), тобто кожна функція вищого рівня декомпозується. Ступінь декомпозиції визначається вимогами до загальної проблеми синтезу системи.
У результаті проведеного аналізу формуються рядки морфологічної таблиці, куди записуються функції системи або її узагальнені функціональні підсистеми. Рядки морфологічної таблиці визначаються із функцій або узагальнених функціональних підсистем, що належать до одного ієрархічного рівня. Найменуваннями стовпців є альтернативи – варіанти реалізації функцій. Отже, у залежності від обраного рівня декомпозиції можна отримати декілька морфологічних таблиць, що із різним ступенем деталізації відображатимуть функціональну структуру системи.
При обробленні морфологічних таблиць на основі функціонального аналізу систем визначають функції підсистем й підбирають для кожної альтернативні конкретні реалізації.
Формування морфологічних таблиць цим способом застосовується, якщо у первинній інформації про систему в явному вигляді функціональні компоненти не виділені, коли фахівці не дуже орієнтуються в предметній області, коли передбачено використовувати лише кількісну експертну оцінку альтернатив за критеріями якості.
Інший спосіб – це синтез морфологічних таблиць із використанням класифікаційних ознак. Він реалізується у наступні два етапи.
На першому реалізується функціональний аналіз. На другому етапі кожна альтернатива із морфологічної таблиці додатково характеризується множиною якісних класифікаційних ознак, що більш ретельно відображають відмінні риси альтернатив. Для цього розробляють для кожної узагальненої функціональної підсистеми класифікацію та описують альтернативи кожної функції відповідними значеннями ознак. Тобто складають класифікаційні образи альтернатив (Табл.10.5).
Таблиця 10.5. Структура морфологічної таблиці з класифікаційними ознаками
| F | A | ||
| F1 | A(1) a1(1) | a1(1) | … ak1(1) |
| G(1) G1(1) | G1(1) | … Gk1(1 | |
| F2 | A(2) a1(2) | a2(2) | … ak2(2) |
| G(1) G1(1) | G2(2) | … Gk2(2) | |
| … | … | … | … |
| Fm | A(m) a1(m) | a2(m) | … akg(m) |
| G(m) G1(m) | G2(m) | … Gkm(m) |
Для кожної функції Fi будується матриця G(i) = (G1(i)G1(i) … G1 (i)), кожний вектор-стовпчик якої Gj(i) = (g 1j(i) g 2j(i) … g d j(i))T відповідає альтернативному варіанту aj(i) реалізації функції Fi, а елемент вектора g 1j(i) – значення 1-ї класифікаційної ознаки j –го варіанту реалізації i –ї функції.
j(i))T відповідає альтернативному варіанту aj(i) реалізації функції Fi, а елемент вектора g 1j(i) – значення 1-ї класифікаційної ознаки j –го варіанту реалізації i –ї функції.
Цей спосіб використовується при наявності попередньо структурованої інформації про системи за функціональними компонентами; при задачі більш глибокого дослідження морфологічної множини варіантів систем та синтезу принципово нових знань про структуру системи; при наявності високопрофесійних фахівців та коли треба дослідити морфологічні множини одночасно за кількісними критеріями якості та якісними ознаками функції та структури варіантів системи.
Системи-класифікації – це результат класифікаційних побудов на множинах об’єктів. Прикладами таких систем є множина описів об’єктів із заданим відношенням еквівалентності; розбиття на класи із заданим відношенням ієрархії або домінування тощо. Системи-класифікації поєднують суб’єктивні та об’єктивні аспекти, тому що класифікуючи, люди оперують обмеженим числом ознак та їх значень.
Основними етапами побудови та дослідження систем-класифікацій є наступні:
· Глибоке проникнення в суть явищ та вибір відповідної класифікації у відповідності до поставленої мети.
· Побудова репрезентативної вибірки об’єктів.
· Визначення сукупності ознак об’єктів шляхом обчислення їх інформативності.
· Завдання відношень між об’єктами та об’єктами і класами шляхом обчислення міри близькості; вирішуючих правил та критеріїв ефективності.
· Побудова й аналіз структурної схеми системи, у якій зв’язки між елементами відповідають відношеннями між ними.
· Перенесення отриманих тверджень із системи-моделі на систему-прототип.
Нехай задана скінчена по необхідності множина X об’єктів, відносно якої розглядається розбиття на систему із K непустих попарно непересічних підмножин Х k, k =  , – класів експертної оцінки об’єктів:
, – класів експертної оцінки об’єктів:
X =  Х k;
Х k; 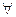 r, q
r, q 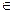 K (Х r ∩ Х k = Ø, r ≠ k).
K (Х r ∩ Х k = Ø, r ≠ k).
Під об’єктом розглядається N -вимірний вектор χ = (χ 1, χ 2,..., χ Ν), компонентами якого є дискретні ознаки та характеристики.
Введемо теоретико-інформаційну міру J (X 1, X 2,..., X K) χ ί величини інформації, що міститься в χ і, ί = 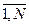 , тобто визначимо величину, що буде вимірювати, як багато інформації створюється χ ί, якщо її використати в якості ознаки об’єкту, при заданому розбитті множини об’єктів X на класи Х k, k =
, тобто визначимо величину, що буде вимірювати, як багато інформації створюється χ ί, якщо її використати в якості ознаки об’єкту, при заданому розбитті множини об’єктів X на класи Х k, k =  .
.
Нехай, далі,
P ( ) @ h l / G k
) @ h l / G k
суть імовірності значення  величини χ ί в класі Х k, k =
величини χ ί в класі Х k, k =
 , розміром G k, але це все, що відомо стосовно χ ί.
, розміром G k, але це все, що відомо стосовно χ ί.
Якщо є така міра, то розумно вимагати, щоб вона володіла наступними властивостями:
(а) J (X 1, X 2,..., X K) χ ί мусить бути неперервною відносно P ( ).
).
(б) У випадку рівних між собою ймовірностей значень, що характеризують об’єкт, із  різних класів, міститься більше невизначеності, ніж у випадку, коли ці імовірності різні.
різних класів, міститься більше невизначеності, ніж у випадку, коли ці імовірності різні.
(в) J (X 1, X 2,..., X K) χ ί повинна бути опуклою функцією, тобто, якщо б визначення міри  інформативності χ ί розпадалося на дві послідовні дії, то первісна J (X 1, X 2,..., X K) χ ί повинна бути зваженою сумою індивідуальних величин.
інформативності χ ί розпадалося на дві послідовні дії, то первісна J (X 1, X 2,..., X K) χ ί повинна бути зваженою сумою індивідуальних величин.
Задана невід’ємна числова функція ψ (P і), i = 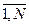 , визначена на опуклій множині дійсних чисел - інтервалі (0, 1):
, визначена на опуклій множині дійсних чисел - інтервалі (0, 1):
ψ (P і)= (K - 1)-1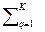
 | P (
| P (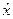 iq
iq ) – P (
) – P (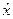 іr)|,
іr)|,
де K - число класів, P (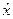 іq) та P (
іq) та P (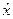 і r) - суть імовірності і - го, і =
і r) - суть імовірності і - го, і = 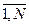 , значення ознаки в класах із індексами q та r відповідно, q ≠ r.
, значення ознаки в класах із індексами q та r відповідно, q ≠ r.
В силу обмеженості ймовірностей функція J (X 1, X 2,..., X K) χ ί є опуклою та J (X 1, X 2,..., X K) χ ί = 0, коли ймовірності рівні; J (X 1, X 2,..., X K) χ ί = 1, коли одна із ймовірностей дорівнює 1, а решта обертається у 0.
Доведено теорему, де стверджується, що величина інформативності J (X 1, X 2,..., X K) χ ί показника χ ί, як функція від P m, буде мати вигляд:
J (X 1, X 2,..., X K) χ ί = K -1 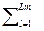 ψ (P l)
ψ (P l)
та наступні властивості:
1. 0 ≤ J (X 1, X 2,..., X K) χ ί ≤ 1.
2. J (X 1, X 2,..., X K) χ ί не змінюється при довільній перестановці своїх аргументів.
3. Безперервно залежить від своїх аргументів.
4. Є опуклою.
Властивості величини інформативності J (X 1, X 2,..., X K) χ ί дозволяють прийняти наступне Означення: Придатність χ ί для використання її в якості ознаки в задачі системної експертної оцінки об’єктів кількісно виражається істотною мірою інформативності J (X 1, X 2,..., X K) χ ί, зв’язаної з поняттям невизначеності значень χ ί таким чином: чим більше невизначеності, тим менше величина інформативності.
Функціональні підсистеми, із котрих складається функціональна система, вносять різний внесок в її ефективність та новизну. Тому окрім оцінювання відносного внеску в ефективність альтернатив, оцінюють відносний внесок й функціональних підсистем.
Це відбувається наступним чином:
1. Будується морфологічна таблиця, рядками якої є узагальнені функціональні підсистеми, а стовпчиками – альтернативи.
2. Морфологічна таблиця перетворюється у трьохрівневу ієрархію, що відображає множину функціональних реалізацій. Фокусом ієрархії є найменування досліджуваної системи. Другий рівень ієрархії утворюють узагальнені функціональні підсистеми (рядки морфологічної матриці). Кожна узагальнена функціональна підсистема конкретизується своєю підмножиною альтернативних функціональних реалізацій (Аi j), що утворюють 3-й рівень ієрархії (Рис. 32).
 |
 |
Рівень 1. Фокус
 |





 Рівень 2.
Рівень 2.
Узагальнені …








 функціональні
функціональні
підсистеми

















 Рівень 3. … … …
Рівень 3. … … …
Альтернативи
w11 w12 … w1k w21 w22 … w2l wn1 wn2 … wnm
Рис.32. Представлення морфологічної таблиці у вигляді трьохрівневої ієрархії
Складаються ієрархічні структури критеріїв якості для визначення векторів пріоритетів узагальнених функціональних підсистем та альтернатив, що конкретизують ці підсистеми.
Для сформованих ієрархій розраховують вектори пріоритетів альтернатив W Ai (i = 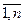 ) кожної узагальненої функціональної підсистеми та вектор W УФПС пріоритетів власне цих підсистем. Останній визначає їх внесок у ефективність та новизну системи у цілому. Значення компонент векторів пріоритетів приписуються відповідним елементам ієрархії.
) кожної узагальненої функціональної підсистеми та вектор W УФПС пріоритетів власне цих підсистем. Останній визначає їх внесок у ефективність та новизну системи у цілому. Значення компонент векторів пріоритетів приписуються відповідним елементам ієрархії.
На базі отриманої інформації виконується ієрархічний синтез за алгоритмом згортання у ієрархіях із декількома гілками, що мають різне число альтернатив. У результаті отримують нормований вектор пріоритетів всіх альтернатив відносно фокусу ієрархії.
Отримані значення векторів пріоритетів альтернатив знову заносяться у відповідні комірки початкової морфологічної таблиці.
Задачу пошуку у морфологічній множині варіантів систем, що наближені до прототипу або до пошукового завдання, можна вирішити на основі міри близькості:
D (B i, B p) → max,
де D (B i, B p) – міра близькості між описом синтезованого варіанта системи B i та прототипом або пошуковим завданням B p.
Морфологічний синтез здійснюється наступним чином:
1. Формують морфологічну таблицю, альтернативи котрої характеризуються множиною ознак.
2. Після визначення прототипу виконують генерацію всіх варіантів із таблиці. Пошукові образи генерованих варіантів порівнюються із образом прототипу.
Для кожної пари „ прототип – пошуковий образ варіанта ” обчислюється значення міри близькості. Підмножина найближчих до прототипу варіантів остаточно надається експерту для детальнішого аналізу.
Приклад 1. (Формування пошукових завдань)
Необхідно сформувати пошукові завдання для системи, заданої наступною морфологічною таблицею:
| F | A | Pr | Pj | Pg | ||
| F1 A(1) Q1(1) Q2(1) Q3(1) | a1(1) | a2(1) | a3(1) | ar1(1) | ||
| 7 | 3 | 9 | 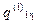
| 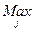 q1j(1) q1j(1)
| qe1(1) | |
| 2 | 8 | 1 | 
| 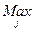 q2j(1) q2j(1)
| qe2(1) | |
| 4 | 2 | 6 | 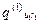
| 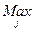 q q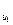 j(1) j(1)
| 
| |
| F2 A(2) Q1(2) Q2(2) | a1(2) | a2(2) | ak2(1) | |||
| 6 | 5 | 
| 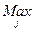 q1j(2) q1j(2)
| qe1(2) | ||
| 3 | 8 | 
| 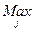 q2j(2) q2j(2)
| qe2(2) | ||
| F3 A(3) Q1(3) | a1(3) | a2(3) | a3(3) | ar3(3) | ||
| 2 | 8 | 4 | 
| 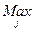 q1j(g) q1j(g)
| 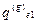
|
Якщо дозволені усі варіанти сполучень реалізацій функцій, то загальна кількість варіантів становитиме
R = ∏I=1nki = 3·2·3.
У цій таблиці не всі комбінації функцій не є припустимими – так, вибір варіанта a 3(1) реалізації функції F1 забороняє вибір варіанта a 2(3)функції F3, а вибір варіанта a 3(1) реалізації функції F2 забороняє вибір варіанта a 3(3)функції F3. Отже, кількість дозволених варіантів становитиме R = 18 – 2 – 3 = 13.
За першим способом пошукове завдання Pr формується безпосередньо на морфологічній таблиці у вигляді комбінацій альтернатив по одній з кожного рядка. Якщо у якості пошукового завдання обрати Pr = (a 3(1) a 2(2) a 2(3)), то реально такий варіант системи не існує (бо вибір варіанта a 3(1) реалізації функції F1 забороняє вибір варіанта a 2(3) функції F3), і задача зводиться до пошуку найближчого припустимого варіанта системи. Якщо ж в якості пошукового завдання обрати Pr = (a 3(1) a 2(2) a 3(3)) ,то це й буде варіант шуканої системи, якість котрого відображатиметься векторами критеріїв для кожної обраної реалізації Q (1) = (Q 1(1) Q 2(1) Q 3(1)) = (9 1 6), Q (2) = (Q 1(2) Q 2(2)) = (8 8), Q (3)= Q 1(3) = 4.
За другим способом пошукове завданняформується у вигляді деякого гіпотетичного ідеального варіанта, елементи котрого, що відповідають рядкам морфологічної таблиці, мають за всіма заданими критеріями якості ідеальні, найкращі граничні властивості. Отже, ідеальному варіанту відповідає образ у просторі критеріїв зі значеннями Q (1) = (9 8 6), Q (2) = (6 8), Q (3)= 8. Реальну систему знаходять, обираючи найближчий до ідеального припустимий варіант.
За третім способом пошукове завдання формується на підставі бажаного для експерта ступеня якості, наприклад Q (1) = (7 2 3), Q (2) = (4 3), Q (3)= = 4.
Приклад 2. (Морфологічна таблиця на основі попарних порівнянь)
Задача: розробити та ухвалити заходи для розвитку інфраструктури міста.
Розв’язок. У результаті попереднього аналізу побудували морфологічну таблицю, де відображені основні можливі альтернативи для кожної узагальненої функціональної підсистеми: пере профілізація та реконструкція промислових підприємств, що має сприяти зниженню рівня безробіття та припливу кваліфікованої робочої сили; основні капіталовкладення залучать туристів та дадуть стійкі джерела прибутку на перспективу; розвиток та вдосконалення транспортної мережі міста.
У наведеній нижче морфологічній таблиці записані результати експертних оцінок у вигляді векторів пріоритетів альтернатив за кожним із критеріїв, що стосуються узагальнених функцій, а також головні власні вектори (важливості) часткових критеріїв відносно загальних. Ця інформація отримана шляхом попарних порівнянь альтернатив за критеріями та попарних порівнянь часткових критеріїв відносно загальних.
| Узагальнена функціональна підсистема | Альтернативи та вектор пріоритетів альтернатив за критеріями | Вага крите-рію | Найменування критерію | ||
| УФПС1 – реконструкція промислових підприємств | а 1(1) – телевізійний завод | а 2(1) – фабрика модного одягу | а 3(1) – харчове підпри- ємство | Q1(1) – робочі місця Q2(1) – окупність Q3(1) – екологія Q0(1) – загальний | |
| РQ 1 (1) = (.26 | .10 | .63)Т | .65 | ||
| РQ 2 (1) ) = (.17 | .74 | .04)Т | .12 | ||
| РQ 3 (1) = (.31 | .58 | .11)Т | .23 | ||
| РQ 0 (1) = (.26 | .29 | .45)Т | |||
| УФПС2 – капітальні вкладення | а 1(2) - готелі | а 2(2) – центр міста | Q1(2) – окупність Q22) – актуальність Q3(2) – робочі місця Q0(2) – загальний | ||
| РQ 1 (2) = (.20 | .80)Т | .33 | |||
| РQ 2 (2) = (.30 | .70)Т | .33 | |||
| РQ 3 (2) = (.30 | .50)Т | .33 | |||
| РQ 0 (2) = (.33 | .66)Т | ||||
| УФПС3 – розвиток транспортної мережі | а 1(3) трамвай | а 2(3) тролейбус | а 3(3) – таксі | Q1(3) – енергоємність Q1(3) – надійність Q3(3) – компактність Q0(3) – загальний | |
| РQ 1 (3) = (.80 | .15 | .05)Т | .23 | ||
| РQ 2 (3) = (.31 | .31 | .11)Т | .12 | ||
| РQ 3 (3) = (.10 | .10 | .26)Т | .65 | ||
| Р Q 0 (3) = (.67 | .14 | .19)Т |
Морфологічна таблиця
Приклад 3. (Синтез варіантів, подібних до прототипу)
У результаті досліджень отримана наступна морфологічна таблиця із якісними ознаками:
| УФПСі | Ознака f ij | Пошукові образи альтернатив | ||
| УФПС1 | f11 f12 f13 f14 f15 | a 11 1 | a 12 0 | a 13 1 -1 |
| УФПС2 | f21 f22 f23 f24 f25 | a 21 0 | a 22 1 | |
| УФПС3 | f31 f32 f33 f34 | a 31 0 | a 32 1 | a 33 0 |
Наявність в альтернативи деякої ознаки позначається одиницею, а відсутність – нулем. Прототип, відносно якого обчислюється міра близькості, задається аналогічно. Припустимо, що прототип синтезований із альтернатив морфологічної таблиці та складається із їх композиції. Далі генерують усі варіанти, що є у наступній таблиці.
Пошукові образи генерованих варіантів порівнюються із образом прототипу.
| УФПСі | Прототип Bn = (a 11 a 21 a 31) | Пошуковий образ синтезованих варіантів (S i1) | |||
| B1 = (a 11 a 21 a 32) B2 = (a 11 a 21 a 33) … B3 = (a 13 a 22 a 33) | |||||
| УФПС1 | 1 0 1 1 0 | … | |||
| УФПС2 | 0 1 1 0 0 | … | |||
| УФПС3 | 0 0 1 1 | … |
Задачу пошуку у морфологічній множині варіантів систем, що наближені до прототипу або до пошукового завдання, вирішується на основі міри близькості:
D (B i, B p) → max,
де D (B i, B p) – міра близькості між описом синтезованого варіанта системи B i та прототипом або пошуковим завданням B p.
Для кожної пари „прототип – пошуковий образ варіанта” обчислюється значення міри близькості. Підмножина найближчих до прототипу варіантів остаточно надається експерту для детальнішого аналізу.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1883; Нарушение авторских прав?; Мы поможем в написании вашей работы!