
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры обработки результатов косвенных измерений
|
|
|
|
 Пример 1 – определение общего сопротивления и погрешности последовательного соединения резисторов
Пример 1 – определение общего сопротивления и погрешности последовательного соединения резисторов
Ø В результате измерений с 10 наблюдениями получено:
| Характеристика | i | ||
| Ri, Ом | 100,00 | 10,00 | 1,00 |
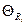 , Ом , Ом
| 0,03 | 0,02 | 0,01 |
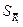 , Ом , Ом
| 0,01 | 0,01 | 0,01 |
Известно, что результаты измерений независимы
 Вычислить результат косвенного измерения
Вычислить результат косвенного измерения
 |
- Вычислить оценку СКО результата косвенного измерения
 | |||
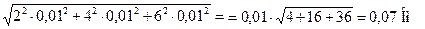 | |||
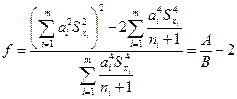 Вычислить число степеней свободы
Вычислить число степеней свободы
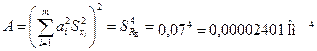 | |||||
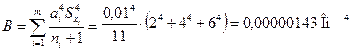 | |||||
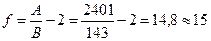 |

 Вычислить доверительные границы случайной составляющей погрешности результата косвенного измерения
Вычислить доверительные границы случайной составляющей погрешности результата косвенного измерения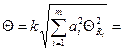 Вычислить доверительные границы неисключенной систематической составляющей погрешности результата косвенного измерения
Вычислить доверительные границы неисключенной систематической составляющей погрешности результата косвенного измерения




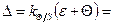 Вычислить доверительные границы погрешности результата косвенного измерения
Вычислить доверительные границы погрешности результата косвенного измерения
Ø Пример 2 – измерение плотности твёрдого тела r= m / V.
Ø Измерение массы тела проведено методом гидростатического взвешивания с применением набора гирь, пределы погрешности которых ±0,01 мг.
Ø Результаты измерений массы в мг: 252,9191; 252,9133; 252,9151; 252,9130; 252,9109; 252,9094; 252,9113; 252,9115; 252,9119; 252,9115; 252,9118.
Ø Измерение объёма тела также проведено методом гидростатического взвешивания с применением того же набора гирь.
Ø Результаты измерений объёма в см3: 195,3799; 195,3830; 195,3790; 195,3819; 195,3795; 195,3788; 195,3792; 195,3794; 195,3791; 195,3791; 195,3794.
| i | 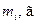
| 
| 
| 
| 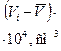
|  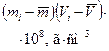
| |
| 252,9119 | -1 | 195,3799 | -1 | ||||
| -8 | -248 | ||||||
| -11 | -3 | ||||||
| -26 | -10 | ||||||
| -7 | -6 | ||||||
| -5 | -4 | ||||||
| -1 | -7 | ||||||
| -7 | -35 | ||||||
| -2 | -4 | ||||||
| S | 2782,032 | 2149,178 |
Ø Различие между результатами наблюдений объясняется случайной погрешностью весов, которая превышает систематические погрешности, обусловленные погрешностями гирь, что ими можно пренебречь.
Ø Вычислим средние арифметические результатов измерений массы и объёма с многократными наблюдениями
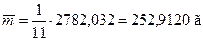
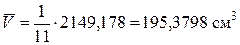
Ø 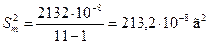 Вычислим дисперсии и СКО случайной составляющей погрешности
Вычислим дисперсии и СКО случайной составляющей погрешности
 | ||
 |
Ø  Проверим результаты измерений на промахи
Проверим результаты измерений на промахи
 |
Ø Следовательно, в результатах наблюдений промахи отсутствуют.
Ø 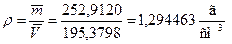 Вычислим результат косвенного измерения
Вычислим результат косвенного измерения
 |
Ø или
Ø  Вычислим оценку коэффициента корреляции
Вычислим оценку коэффициента корреляции
Ø 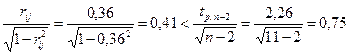 Проверим значимость коэффициента корреляции
Проверим значимость коэффициента корреляции
Ø 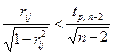 Следовательно, корреляцией в измерениях массы и объёма можно пренебречь, т.к.
Следовательно, корреляцией в измерениях массы и объёма можно пренебречь, т.к.
Ø 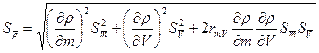 Для вычисления оценки СКО результата косвенного измерения
Для вычисления оценки СКО результата косвенного измерения
Ø 
 вычислим частные производные
вычислим частные производные
Ø  Вычислим оценки частных производных в окрестности точки 1294,463 кг/м3
Вычислим оценки частных производных в окрестности точки 1294,463 кг/м3
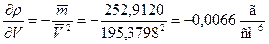 |
Ø 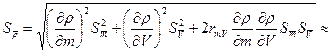 Вычислим оценку СКО результата косвенного измерения
Вычислим оценку СКО результата косвенного измерения
 |
Ø 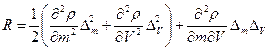 Для вычисления остаточного члена ряда Тейлора
Для вычисления остаточного члена ряда Тейлора
Ø 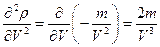
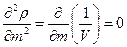 вычислим частные производные
вычислим частные производные
 |
Ø Вычислим оценки частных производных в окрестности точки 1294,463 кг/м3
 |  |
Ø 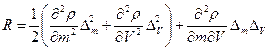 Вычислим остаточный член ряда Тейлора
Вычислим остаточный член ряда Тейлора
Ø  В качестве D m и D V используем наибольшие отклонения результатов наблюдений от оценок средних значений. Примечание – поскольку погрешности случайные, то знак погрешности не следует фиксировать!
В качестве D m и D V используем наибольшие отклонения результатов наблюдений от оценок средних значений. Примечание – поскольку погрешности случайные, то знак погрешности не следует фиксировать!
 |
Ø Откуда
Ø 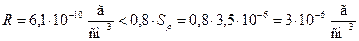 Проверим значимость остаточного члена ряда Тейлора
Проверим значимость остаточного члена ряда Тейлора
Ø 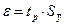 Следовательно, применять линеаризацию допустимо.
Следовательно, применять линеаризацию допустимо.
Ø  Для вычисления доверительных границ случайной составляющей погрешности определим число степеней свободы
Для вычисления доверительных границ случайной составляющей погрешности определим число степеней свободы
 | |||||||
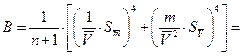 | |||||||
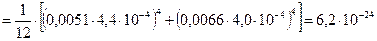 | |||||||
 |
Ø  Вычислим доверительные границы случайной составляющей погрешности
Вычислим доверительные границы случайной составляющей погрешности
Ø Поскольку систематические составляющие погрешности измерений массы и объёма пренебрежимо малы, то и систематическая составляющая погрешности измерений плотности также пренебрежимо мала.
Ø 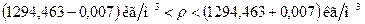
 Таким образом, результат измерений плотности с доверительной вероятностью 0,95 находится в интервале
Таким образом, результат измерений плотности с доверительной вероятностью 0,95 находится в интервале
 |
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 961; Нарушение авторских прав?; Мы поможем в написании вашей работы!