
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема: Діелектрики в електричному полі. Поляризація діелектриків. Вектор поляризованості. Діелектрична проникливість. Умови на границі розділу діелектриків
|
|
|
|
Лекція № 23.
Діелектриками називають речовини, які практично не проводять електричного струму. Це означає, що в діелектриках на відміну від провідників немає зарядів, здатних переміщатися на значні відстані, створюючи струм. Молекули діелектриків можуть бути полярними і неполярними. У полярних молекул центр «ваги» негативного заряду зміщений щодо центра «ваги» позитивних зарядів, у результаті чого вони мають власний дипольний момент 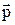 . Неполярні молекули власним дипольним моментом не володіють: у них центри «ваги» позитивного і негативного зарядів збігаються. Під дією зовнішнього електричного поля відбувається поляризація діелектрика. Це явище полягає в наступному. Якщо діелектрик складається з неполярних молекул, то в межах кожної молекули відбувається зсув зарядів – позитивних по полю, негативних проти поля. Якщо діелектрик складається з полярних молекул, то при відсутності зовнішнього поля їхні дипольні моменти внаслідок теплового руху орієнтовані хаотично. Під дією зовнішнього поля дипольні моменти орієнтуються переважно в напрямку зовнішнього поля. Це приводить до зсуву електричних зарядів: позитивних по полю, а негативних – проти поля. У результаті поляризації на поверхні діелектрика та у його об’ємі з'являються нескомпенсовані заряди, які називають поляризованими або зв'язаними. Поляризовані заряди можуть зміщатися лише усередині електрично нейтральних молекул. Заряди, що не входять до складу молекул діелектрика, називають сторонніми. Ці заряди можуть знаходитися як усередині, так і поза діелектриком.
. Неполярні молекули власним дипольним моментом не володіють: у них центри «ваги» позитивного і негативного зарядів збігаються. Під дією зовнішнього електричного поля відбувається поляризація діелектрика. Це явище полягає в наступному. Якщо діелектрик складається з неполярних молекул, то в межах кожної молекули відбувається зсув зарядів – позитивних по полю, негативних проти поля. Якщо діелектрик складається з полярних молекул, то при відсутності зовнішнього поля їхні дипольні моменти внаслідок теплового руху орієнтовані хаотично. Під дією зовнішнього поля дипольні моменти орієнтуються переважно в напрямку зовнішнього поля. Це приводить до зсуву електричних зарядів: позитивних по полю, а негативних – проти поля. У результаті поляризації на поверхні діелектрика та у його об’ємі з'являються нескомпенсовані заряди, які називають поляризованими або зв'язаними. Поляризовані заряди можуть зміщатися лише усередині електрично нейтральних молекул. Заряди, що не входять до складу молекул діелектрика, називають сторонніми. Ці заряди можуть знаходитися як усередині, так і поза діелектриком.
Напруженістю поля Е в діелектрику називається величина, яка є суперпозицією поля Е0 сторонніх зарядів і поля Е' зв'язаних зарядів:
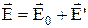 .
.
де 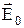 і
і 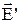 являють собою усереднені по фізично нескінченно малому об’єму напруженості відповідно сторонніх і зв'язаних зарядів.
являють собою усереднені по фізично нескінченно малому об’єму напруженості відповідно сторонніх і зв'язаних зарядів.
Для кількісного опису явища поляризації діелектрика вводять вектор поляризованості 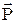 , що визначається як дипольний момент одиниці об'єму речовини:
, що визначається як дипольний момент одиниці об'єму речовини:
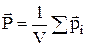 ,
,
де 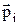 – дипольний момент і-го диполя. Нехай в об’ємі V утримується N диполів концентрація яких визначається з вираження:
– дипольний момент і-го диполя. Нехай в об’ємі V утримується N диполів концентрація яких визначається з вираження: 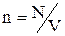 . Тоді можна записати:
. Тоді можна записати:
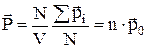 ,
,
де 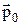 – середній дипольний момент однієї молекули.
– середній дипольний момент однієї молекули.
Одиниці поляризованості. Виділимо дуже малий об’єм dV усередині діелектрика. При виникненні поляризації позитивний заряд, що входить у цей об’єм 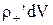 зміститься щодо негативного заряду на величину 1, і ці заряди придбають дипольний момент
зміститься щодо негативного заряду на величину 1, і ці заряди придбають дипольний момент 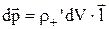 . Розділивши обидві частини цієї рівності на dV, одержимо вираження для дипольного моменту одиниця об'єму, тобто вектор поляризованості
. Розділивши обидві частини цієї рівності на dV, одержимо вираження для дипольного моменту одиниця об'єму, тобто вектор поляризованості 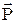 :
: 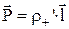 . З отриманої формули випливає, що одиницею поляризованості в СІ є [Кл/м2].
. З отриманої формули випливає, що одиницею поляризованості в СІ є [Кл/м2].
Зв'язок між векторами напруженості і поляризованості. Дослід показує, що для більшості діелектриків поляризованість лінійно залежить від напруженості поля: 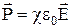 , де c – безрозмірна величина, що називається діелектричною сприйнятливістю речовини. Діелектрична сприйнятливість не залежить від поляризованості, а визначається тільки властивостями діелектрика.
, де c – безрозмірна величина, що називається діелектричною сприйнятливістю речовини. Діелектрична сприйнятливість не залежить від поляризованості, а визначається тільки властивостями діелектрика.
Властивості поля вектора поляризованості.
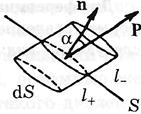 Нехай довільна замкнута поверхня S охоплює частину діелектрика. При включенні зовнішнього електричного поля діелектрик поляризується – позитивні заряди зміщуються щодо негативних. Знайдемо заряд, що проходить через елемент dS замкнутої поверхні S назовні. Нехай 1+ і l- – вектори, що характеризують зсуви позитивних і негативного зв'язаних зарядів у результаті поляризації. Тоді через елемент поверхні dS назовні поверхні S вийде позитивний заряд
Нехай довільна замкнута поверхня S охоплює частину діелектрика. При включенні зовнішнього електричного поля діелектрик поляризується – позитивні заряди зміщуються щодо негативних. Знайдемо заряд, що проходить через елемент dS замкнутої поверхні S назовні. Нехай 1+ і l- – вектори, що характеризують зсуви позитивних і негативного зв'язаних зарядів у результаті поляризації. Тоді через елемент поверхні dS назовні поверхні S вийде позитивний заряд  , що знаходиться у внутрішній частині косого циліндра. Крім того, через елемент dS ввійде усередину поверхні S негативний заряд
, що знаходиться у внутрішній частині косого циліндра. Крім того, через елемент dS ввійде усередину поверхні S негативний заряд 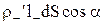 , який знаходиться у зовнішній частині косого циліндра. Але перенос негативного заряду в деякому напрямку еквівалентний переносу позитивного заряду в протилежному напрямку, унаслідок чого сумарний зв'язаний заряд, що виходить назовні поверхні S через елемент dS, дорівнює:
, який знаходиться у зовнішній частині косого циліндра. Але перенос негативного заряду в деякому напрямку еквівалентний переносу позитивного заряду в протилежному напрямку, унаслідок чого сумарний зв'язаний заряд, що виходить назовні поверхні S через елемент dS, дорівнює:
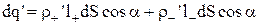 .
.
Враховуючи, що 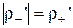 , остаточно одержуємо:
, остаточно одержуємо:
 ,
,
де 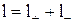 – відстань, на яку зміщаються відносно один одного позитивні і негативні зв'язані заряди діелектрика при поляризації. З огляду на те, що
– відстань, на яку зміщаються відносно один одного позитивні і негативні зв'язані заряди діелектрика при поляризації. З огляду на те, що 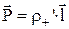 , після відповідної заміни одержуємо:
, після відповідної заміни одержуємо:
 .
.
Проінтегрувавши це вираження по всій замкнутій поверхні S, ми знайдемо весь заряд, що вийшов при поляризації з об’єму, охоплюваного поверхнею S. У результаті усередині поверхні S залишиться деякий надлишковий зв'язаний заряд q'. Ясно, що заряд, який вийшов, повинний дорівнює зі зворотним знаком надлишковому зв'язаному заряду, що залишився усередині поверхні S, тобто:
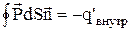 .
.
Отримане рівняння виражає теорему Гаусса для вектора поляризованості: потік вектора 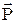 крізь довільну замкнуту поверхню S дорівнює узятому зі зворотним знаком надлишковому зв'язаному заряду діелектрика в об’ємі, охоплюваному поверхнею S.
крізь довільну замкнуту поверхню S дорівнює узятому зі зворотним знаком надлишковому зв'язаному заряду діелектрика в об’ємі, охоплюваному поверхнею S.
У диференціальній формі отримане рівняння має вигляд:
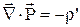 ,
,
тобто дивергенція поля вектора 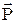 дорівнює зі зворотним знаком об'ємної густині надлишкового зв'язаного заряду в тій же точці.
дорівнює зі зворотним знаком об'ємної густині надлишкового зв'язаного заряду в тій же точці.
Оскільки в загальному випадку джерелами поля Е є всі електричні заряди – стороння і зв'язані, то теорема Гаусса для поля Е приймає вигляд:
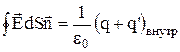 или
или 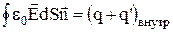 ,
,
де q і q' – сторонні і зв'язані заряди, що охоплюються поверхнею S. Але, оскільки 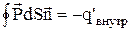 , то після відповідної заміни одержуємо:
, то після відповідної заміни одержуємо:
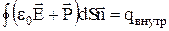 .
.
Введемо допоміжний вектор 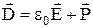 – електричний зсув. Теорема Гаусса для вектора електричного зсуву має вигляд:
– електричний зсув. Теорема Гаусса для вектора електричного зсуву має вигляд:
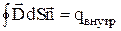 .
.
Потік вектора електричного зсуву крізь довільну замкнуту поверхню дорівнює алгебраїчній сумі зарядів, що охоплюються цією поверхнею.
Зв'язок між векторами D і Е.
У випадку ізотропних діелектриків поляризованість 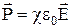 . Підставивши це співвідношення в рівняння
. Підставивши це співвідношення в рівняння 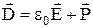 , одержимо:
, одержимо: 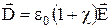 , або
, або 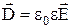 , де e – діелектрична проникність речовини:
, де e – діелектрична проникність речовини: 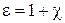 . Діелектрична проникність є основною електричною характеристикою діелектрика. Для всіх речовин e > 1, для вакууму e = 1. Значення e залежать від природи діелектрика.
. Діелектрична проникність є основною електричною характеристикою діелектрика. Для всіх речовин e > 1, для вакууму e = 1. Значення e залежать від природи діелектрика.
Поле вектора D наочно можна зобразити за допомогою ліній вектора D, напрямок і густота яких визначаються так само, як і для ліній вектора Е. Лінії вектора Е можуть починатися і закінчуватися як на сторонніх, так і на зв'язаних зарядах. Джерелами і стоками поля вектора D є тільки сторонні заряди: тільки на них можуть починатися і закінчуватися лінії вектора D. Через області поля, де знаходяться зв'язані заряди, лінії вектора D проходять не перериваючись.
Умови на границі двох діелектриків.
Нехай на границі розділу двох діелектриків знаходиться поверхневий сторонній заряд. Терема про циркуляції вектора напруженості і теорема Гаусса для вектора 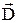 мають вигляд:
мають вигляд:
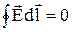 и
и 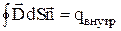 .
.
 Умова для вектора
Умова для вектора 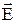 . Нехай поле поблизу межі розділу в діелектрику 1 дорівнює
. Нехай поле поблизу межі розділу в діелектрику 1 дорівнює 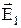 , а в діелектрику 2 –
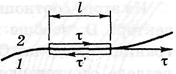
, а в діелектрику 2 – 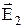 . Візьмемо невеликий витягнутий прямокутний контур зневажливо малої товщини. Відповідно до теореми про циркуляції вектора напруженості
. Візьмемо невеликий витягнутий прямокутний контур зневажливо малої товщини. Відповідно до теореми про циркуляції вектора напруженості 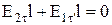 , де проекції вектора напруженості узяті на напрямок обходу контуру, зазначений на малюнку стрілками. Якщо на нижній ділянці контуру проекцію вектора
, де проекції вектора напруженості узяті на напрямок обходу контуру, зазначений на малюнку стрілками. Якщо на нижній ділянці контуру проекцію вектора 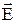 взяти не на орт
взяти не на орт 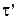 а на загальний орт t, то
а на загальний орт t, то 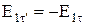 і
і  , тобто тангенціальна складова вектора напруженості виявляється однаковою по обидві сторони межі розділу.
, тобто тангенціальна складова вектора напруженості виявляється однаковою по обидві сторони межі розділу.
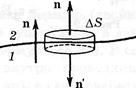 Умова для вектора
Умова для вектора 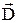 . Візьмемо дуже малої висоти циліндр, розташувавши його на границі розділу двох діелектриків. Перетин циліндра повинен бути таким, щоб у межах кожного його торця вектор
. Візьмемо дуже малої висоти циліндр, розташувавши його на границі розділу двох діелектриків. Перетин циліндра повинен бути таким, щоб у межах кожного його торця вектор 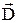 був однаковий. Тоді відповідно до теореми Гаусса для вектора D
був однаковий. Тоді відповідно до теореми Гаусса для вектора D 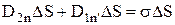 , де s – поверхнева густина стороннього заряду на межі розділу. Взявши обидві проекції вектора
, де s – поверхнева густина стороннього заряду на межі розділу. Взявши обидві проекції вектора 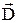 на загальну нормаль
на загальну нормаль 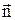 , одержимо:
, одержимо: 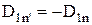 , і попереднє рівняння здобуває вигляд:
, і попереднє рівняння здобуває вигляд:
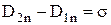 .
.
З отриманого рівняння випливає, що нормальна складового вектора 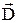 перетерплює стрибок при переході межі розділу. Однак, якщо сторонні заряди на межі розділу відсутні, то в цьому випадку нормальна складова вектора
перетерплює стрибок при переході межі розділу. Однак, якщо сторонні заряди на межі розділу відсутні, то в цьому випадку нормальна складова вектора 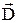 стрибка не випробовує, вона виявляється однаковою по різні сторони межі розділу.
стрибка не випробовує, вона виявляється однаковою по різні сторони межі розділу.
Враховуючи, що 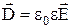 , одержуємо:
, одержуємо: 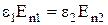 або
або 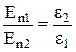 і
і  або
або 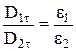 .
.
Таким чином, якщо на межі розділу двох однорідних ізотропних діелектриків сторонніх зарядів немає, то при переході цієї границі складові  і
і  змінюються безперервно, без стрибка, а складові
змінюються безперервно, без стрибка, а складові 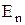 і
і 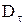 перетерплюють стрибок.
перетерплюють стрибок.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1945; Нарушение авторских прав?; Мы поможем в написании вашей работы!