Постійний електричний струм

Електричним струмом називають упорядкований перенос електричних зарядів. Для існування струму необхідна наявність електричного поля, оскільки при його відсутності вільні заряди рухаються хаотично і безупорядковано, а наявність поля викликає появу електричної сили, що діє на заряди і викликає їхній упорядкований рух. Кількісною мірою електричного струму служить сила струму І, тобто заряд, перенесений крізь розглянуту поверхню S в одиницю часу:

І = dq/dt.

Одиницею сили струму є ампер (А).

Густина струму. Електричний струм може бути розподілений по поверхні, через яку він протікає, нерівномірно. Тому для більш детальної характеристики струму вводять вектор густини струму . Модуль цього вектора чисельно дорівнює відношенню сили струму dІ через елементарну площадку, яка розташовану в даній точці перпендикулярно напрямкові руху носіїв, до її площі dS:

За напрямок вектора приймають напрямок вектора швидкості 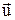упорядкованого руху позитивних носіїв. Якщо носіями є як позитивні, так і негативні заряди, то густина струму визначається формулою:

,

де і – об'ємні густини позитивного і негативного зарядів–носіїв; 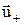і – швидкості їхнього упорядкованого руху. У провідниках, де носіями є тільки електрони, густина струму визначається за формулою: 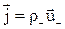. Поле вектора можна зобразити графічно за допомогою ліній струму, що проводять так само, як і лінії вектора напруженості. Знаючи вектор густини струму в кожній точці цікавлячої нас поверхні S, можна знайти силу струму через цю поверхню, як потік вектора j:

.

Сила струму є величиною скалярною й алгебраїчною. Її знак, як видно з формули, визначається вибором напрямку нормалі в кожній точці поверхні S, тобто вибором напрямку векторів . При зміні напрямку усіх векторів на протилежний величина І змінює знак.

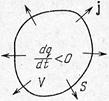Рівняння безперервності. Нехай у деякому провідному середовищі, де тече струм, знаходиться замкнута поверхня S. Інтеграл 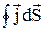являє собою заряд, що виходить в одиницю часу назовні з об’єму V, що охоплюється поверхнею S. За законом збереження заряду цей інтеграл дорівнює збитку заряду в одиницю часу усередині об’єму V:

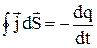
Це співвідношення називають рівнянням безперервності. Воно є математичним вираженням закону збереження електричного заряду. У випадку постійного струму розподіл зарядів у просторі повинний залишатися незмінним, тобто dq = 0 і рівняння безперервності здобуває вигляд:

,

інакше кажучи, лінії вектора в цьому випадку ніде не починаються і ніде не закінчуються. З останнього вираження також випливає, що у випадку постійного струму поле вектора не має джерел.

Диференціальна форма рівняння безперервності. Перетворимо останні два рівняння до диференціальної форми. Для цього представимо заряд q як 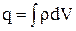. Підставивши формулу заряду в рівняння безперервності, одержимо:

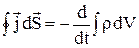або .

Розділимо обидві частини отриманого рівняння на об’єм і спрямуємо його до нуля. У підсумку одержуємо:

або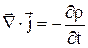

Якщо , то одержуємо умову стаціонарності: 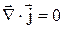, яке означає, що у випадку постійного струму поле вектора не має джерел.

Закон Ома для однорідного провідника. Закон Ома, відкритий експериментально, формулюється наступним чином: сила струму, що протікає по однорідному провіднику, пропорційна різниці потенціалів на його кінцях:

,

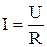де R – електричний опір провідника. Одиницею опору служить Ом. Опір залежить від форми і розмірів провідника, від його матеріалу і температури, а також від конфігурації струму по провіднику. У найпростішому випадку однорідного циліндричного провідника опір визначається за формулою:

,

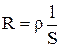де l – довжина провідника; S – площа його поперечного перерізу; r – питомий електричний опір, який залежить від матеріалу провідника і його температури. Виражають r в ом–метрах (Ом*м).

Закон Ома в локальній формі. Знайдемо зв'язок між густиною струму і напруженістю електричного поля в одній і тій же точці провідного середовища. Нехай в ізотропному провіднику напрямки векторів і збігаються. Виділимо думкою в околиці деякої точки провідного середовища елементарний циліндричний об’єм з утворюючими, які паралельні вектору , а значить, і вектору . Якщо поперечний переріз циліндра dS, а його довжина dl, то можна записати: , и 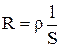. Після відповідних підстановок одержуємо: або у векторному вигляді: . Величина, що зворотна питомому електричному опору, називається питомою електричною провідністю і виміряється в сименсах (См): 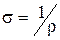. Внаслідок заміни одержуємо закон Ома в локальній формі:

Він встановлює зв'язок між величинами, що відносяться до одній і тій же точці провідного середовища.

Дата добавления: 2014-01-07