Тема: Енергія електричного поля. Постійний електричний струм. Основні характеристики струму. Рівняння безперервності. Закон Ома для однорідного провідника

Лекція № 24

Потенціальна енергія системи зарядів. Розглянемо систему з трьох точкових зарядів. Повна енергія системи має вигляд:

W = W₁₂ + W₁₃ + W₂₃.

Представимо кожен доданок W_іk цієї суми в симетричному вигляді: W_іk = (W_іk+ W_kі)/2, оскільки W_lk = W_kі. Тоді:

W = (W₁₂ + W_2l + W₁₃ + W_3l + W₂₃ + W₃₂)/2.

Згрупуємо члени з однаковими першими індексами:

W = [(W₁₂ + W₁₃) + (W_2l + W₂₃) + (W_3l + W₃₂)]/2.

Кожний доданок в круглих дужках – це енергія W_і взаємодії і-го заряду з іншими зарядами. Тому останнє вираження можна переписати так:

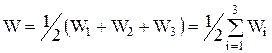
Узагальнимо отриману формулу на систему, що складається з довільної кількості зарядів:

.

Враховуючи, що де q_і – і-й заряд системи; – потенціал, що створюється у місці перебування і-го заряду всіма іншими зарядами системи, одержимо остаточний вираз для енергії взаємодії системи точкових зарядів:

.

Якщо заряди розподілені безперервно, то, розкладаючи систему зарядів на сукупність елементарних зарядів і переходячи від підсумовування до інтегрування, одержуємо:

,

де 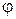– потенціал, що створюється усіма зарядами системи в елементі об’єму dV. При розподілі зарядів по поверхні остання формула здобуває вигляд:

.

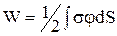Енергія відокремленого провідника. Нехай провідник має заряд q і потенціал j. Оскільки значення потенціалу у всіх точках, де мається заряд, однаково, його можна винести із під знака інтеграла у формулі енергії. Тоді інтеграл, що залишився, є не що інше, як заряд q на провіднику. В остаточному підсумку одержуємо: 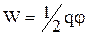. З урахуванням того, що , можна одержати інші формули енергії відокремленого провідника: .

Енергія конденсатора. Енергія конденсатора складається з енергій двох обкладок: . Але 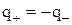, внаслідок чого одержуємо:

,

де U – різниця потенціалів між обкладками конденсатора. Прийнявши до уваги, що С = q/U, одержимо наступні вираження для енергії конденсатора:

.

Варто помітити, що отримані формули визначають повну енергію взаємодії, тобто не тільки енергію взаємодії зарядів однієї обкладки з зарядами іншої, але й енергію взаємодії зарядів усередині кожної обкладки.

Об'ємна густина енергії електрополя. Визначимо енергію електрополя в одиниці об'єму. Нехай електричне поле однорідне, тобто створюється пластинами плоского конденсатора. Тод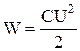і: , , і . Після підстановки одержуємо: . Враховуючи, що , можна записати: . Якщо поле неоднорідне, то формулу енергії можна представити в такому вигляді:

.

Об'ємною густиною енергії називається енергія, що зосереджена в одиниці об'єму, тобто . З урахуванням отриманих формул маємо:

.

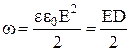Дата добавления: 2014-01-07