Тема. Закон електромагнітної індукції. Правило Ленца. Явище самоіндукції. Енергія магнітного поля

Лекція № 29

Контрольні запитання

1. Які особливості одиничного методу ТО автомобілів?

2. Які особливості потокового методу ТО автомобілів?

3. Що беруть до уваги при виборі методу ТО автомобілів?

4. Як розрахувати параметри потокової лінії ТО автомобілів?

5. Як визначити потрібну кількість робочих постів для ТО і поточного ремонту авто­мобілів на ВАТ АТП?

6. Які особливості індивідуального й агрегатного методів ремонту автомобілів?

7. Які перспективи потокового обслуговування автомобілів?

У 1831 р. М. Фарадей відкрив явище електромагнітної індукції, яке полягає в тім, що в замкнутому провідному контурі при зміні магнітного потоку, охоплюваного цим контуром, виникає електричний струм – його назвали індукційним. Поява індукційного струму означає, що при зміні магнітного потоку в контурі виникає е.р.с. індукції e_i. При цьому було встановлено, що величина e_i не залежить від того, яким чином здійснюється зміна магнітного потоку Ф, а визначається лише швидкістю його зміни, тобто величиною . Крим того, зміна знака похідної приводить до зміни знака або «напрямку» e_i. Напрямок індукційного струму визначається правилом Ленца: індукційний струм завжди спрямований так, щоб протидіяти причині, яка його зухвалює. Інакше кажучи, індукційний струм створює магнітний потік, що перешкоджає зміні магнітного потоку, що викликає е.р.с. індукції.

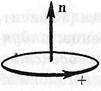Явище електромагнітної індукції покладено в основу закона електромагнітної індукції: Е.Р.С. індукції, яка виникає в замкнутому контурі, який знаходиться у магнітному полі, прямо пропорційна швидкості зміни магнітного потоку, що пронизує контур: 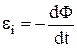. Знак мінус у цьому рівнянні зв'язаний з правилом знаків. Оскільки магнітний потік визначається за формулою 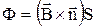, його враховують позитивним, якщо він співпадає з вектором 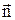до контуру, при цьому вектор нормалі і позитивний напрямок обходу зв’язані один з іншим правилом правого гвинта. Знак зв’язаний з вектором зміни магнітного потоку. Якщо замкнутий контур, у якому індуцірується е.р.с., складається не з одного витка, а з N витків, то буде дорівнює сумі е.р.с, що індуціруються у кожному з витків. І якщо магнітний потік, охоплюваний кожним витком, однаковий і дорівнює Ф₁, то сумарний потік Ф крізь поверхню, натягнуту на такий складний контур, можна представити як: . Цю величину називають повним магнітним потоком або потокозчепленням. У цьому випадку відповідна е.р.с. індукції в контурі визначається згідно формулою .

Природа електромагнітної індукції. Розглянемо послідовно два випадки.

1. Контур рухається в постійному магнітному полі. Насамперед звернемося до контуру з рухливою перемичкою довжиною l. Нехай він знаходиться в однорідному магнітному полі, перпендикулярному площині контуру і спрямованому за площину малюнка. Почнемо рухати перемичку вправо зі швидкістю v. З такою же швидкістю почнуть рухатися і носії струму в перемичці - електрони. У результаті на кожен електрон почне діяти уздовж перемички магнітна сила , і електрони почнуть переміщатися по перемичці вниз, тобто потече індукційний струм, спрямований вгору. Заряди, що перерозподілилися, створять електричне поле, що збудить струм і в інших ділянках контуру. Магнітна сила 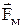відіграє роль сторонньої сили. Оскільки , і , то після відповідних замін отримаємо: 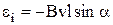. Знак мінус поставлений у зв'язку з правилом знаків: нормаль n до поверхні, натягнутої на наш контур, обираємо за площину рисунку, і тому за правилом правого гвинта позитивний напрямок обходу контуру – по годинній стрілці. При цьому стороннє поле 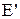спрямоване проти позитивного напрямку обходу контуру і – величина негативна. Добуток vl у формулі е.р.с. є збільшення площі, обмеженої контуром, в одиницю часу , тому , де dФ - збільшення магнітного потоку крізь площу контуру. Таким чином, 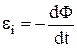. Можна в загальному вигляді довести, що закон електромагнітної індукції справедливий для будь-якого контуру, що рухається довільним образом у постійному неоднорідному магнітному полі. Отже, виникнення е.р.с. індукції при русі контуру в постійному магнітному полі обумовлене дією магнітної сили, що діє на заряди в провіднику при його русі.

2. Контур не рухається в змінному магнітному полі. Виникнення індукційного струму і у цьому випадку свідчить про те, що магнітне поле, яке змінюється з часом, викликає в контурі появу сторонніх сил. Максвелл припустив, що в цьому випадку в просторі виникає електричне поля незалежно від наявності провідного контуру. Останній лише дозволяє знайти по виникненню в ньому індукційного струму існування цього електричного поля. Таким чином, відповідно до Максвелла магнітне поле, що змінюється з часом, породжує електричне поле. Циркуляція вектора напруженості цього поля по будь-якому нерухомому контуру визначається як 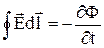. Тут символ похідної за часом 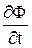підкреслює той факт, що контур і натягнута на нього поверхня нерухомі. Оскільки потік 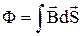, то і . 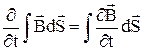Із отриманого рівняння свідчить, що циркуляція вектора напруженості 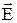, що збуджується змінним магнітним полем, відмінна від нуля. Це означає, що електричне поле не потенційно, воно, як і магнітне поле, є вихровим.

Висновок: При будь якій зміні магнітного поля у просторі виникає вихрове електричне поле, яке у замкненому контурі, що знаходиться в даній точці простору, збуджує індукційний струм.

Явище самоіндукції. Електромагнітна індукція виникає у всіх випадках, коли змінюється магнітний потік крізь контур. При цьому зовсім не важливо, чим викликається ця зміна потоку. Якщо в деякому контурі тече струм, що змінюється в часі, то магнітне поле цього струму також буде змінюватися. Це спричиняє зміну магнітного потоку через контур, а отже, і появу е.р.с. індукції. Таким чином, зміна струму в контурі веде до виникнення е.р.с. індукції в цьому ж самому контурі. Дане явище називають самоіндукцією. Якщо в просторі, де знаходиться контур зі струмом, немає феромагнетиків, поле вектора , а виходить, і повний магнітний потік Ф через контур будуть пропорційні силі струму (Ф~I), і можна записати: , де L – коефіцієнт, називаний індуктивністю контуру. Індуктивність L залежить від форми і розмірів контуру, а також від магнітних властивостей навколишнього середовища. Якщо контур твердий і поблизу від нього немає феромагнетиків, індуктивність є величиною постійною, що не залежить від сили струму. Одиницею індуктивності є Генрі (Гн). Індуктивністю 1 Гн володіє контур, магнітний потік крізь який при струмі 1 А дорівнює 1 Вб. 1 Гн = 1 Вб/А.

Е.Р.С. самоіндукції з урахуванням індуктивності можна представити наступним чином: 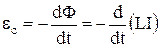. Якщо індуктивність контуру не змінюється, то 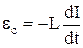. Знак мінус показує, що завжди спрямована так, щоб перешкоджати зміні сили струму. Ця е.р.с. прагне зберегти струм незмінним: вона протидіє току, коли він збільшується, і підтримує струм, коли він зменшується. У явищах самоіндукції струм володіє "інерцією", тому що ефекти індукції прагнуть зберегти магнітний потік постійним, точно так само, як механічна інерція прагне зберегти швидкість тіла незмінною.

Енергія магнітного поля струму. Замкнемо нерухоме електричне коло, що містить індуктивність L і опір R, на джерело струму з е.р.с. 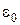. У контурі почне зростати струм. Це приводить до появи е.р.с. самоіндукції . Відповідно до закону Ома , відкіля 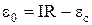. Знайдемо елементарну роботу, яку виконують сторонні сили за час dt. Для цього помножимо попередню рівність на Іdt: 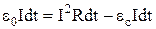. З огляду на зміст кожного доданка і співвідношення , запишемо: 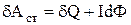. З отриманого рівняння свідчить, що в процесі встановлення струму, коли потік Ф міняється і dФ> 0, робота, яку виконує джерело, виявляється більше виділюваної в колі джоулевої теплоти. Частина цієї роботи відбувається проти е.р.с. самоіндукції. Після того як струм встановиться, dФ = 0 і вся робота джерела буде іти тільки на виділення джоулевої теплоти. Отже, додаткова робота, чинена сторонніми силами проти е.р.с. самоіндукції в процесі встановлення . Оскільки при відсутності феромагнетику 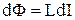, то отримуємо: . Проінтегрував це рівняння при зміні струму від нуля до I, одержимо: 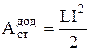. За законом збереження енергії будь-яка робота йде на збільшення енергії. Частина роботи сторонніх сил йде на збільшення внутрішньої енергії провідників, а інша частина – у процесі встановлення струму – на виникнення магнітного поля. Таким чином, можна зробити висновок, що при відсутності феромагнетиків контур з індуктивністю L, по якому тече струм I, має енергію , яку називають енергією магнітного поля струму.

Енергія магнітного поля довгого соленоїда зі струмом. Соленоїд – це одношарова котушка довжиною l площею перерізу S. 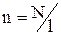– число ампер витків, тобто число витків на одиницю довжини соленоїда. Визначимо індуктивність соленоїда. Оскільки , і 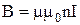, то отримаємо: , де 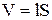– об’єм соленоїда. Підставимо отриманий вираз у формулу енергії магнітного поля: 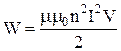. За теоремою про циркуляцію вектора напруженості магнітного поля можна записати: або 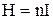. Зробивши заміну в формулі енергії магнітного поля, отримуємо: 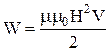. 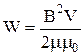Враховуючи, що , можна записати: або .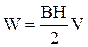

Об’ємною густиною енергії магнітного поля називають енергію одиниці об’єму простору: .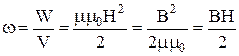

Дата добавления: 2014-01-07