
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры обработки результатов совокупных измерений
|
|
|
|
Ø Пример 1
Ø Передача размера единицы массы 1 кг килограммовому набору гирь КГ-2-20, состоящему из гирь 10, 5, 2, 2 и 1 кг
Ø  Пусть – значение массы эталона;
Пусть – значение массы эталона;
Ø – значения масс гирь.
Ø Примечание
Ø Звёздочкой отмечена вторая гиря того же номинала.
Ø Определение массы гирь производят взвешиванием
на равноплечих весах с применением вспомогательных гирь, используемых для уравновешивания весов.
Ø Примечание
Ø При определении массы гирь 2 разряда учитывают поправки
на неисключенную систематическую погрешность гирь 1 разряда (согласно МИ 1747-87 ГСИ. Меры массы образцовые и общего назначения. Методика поверки)
Ø 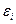 В результате будут получены:
В результате будут получены:
Ø значения сумм масс вспомогательных гирь
в каждом из сличений;
Ø система из n линейных уравнений с n неизвестными
 |  | ||
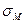 |
Ø 

 Определим СКО масс гирь при известных СКО эталона и СКО устройства сравнения (компаратора).
Определим СКО масс гирь при известных СКО эталона и СКО устройства сравнения (компаратора).
Ø 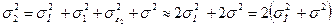
 Из следует
Из следует
Ø Из следует
Ø 
 Аналогично:
Аналогично:
 | |||
 |
Ø Таким образом:
Ø 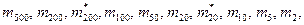 Пример 2 Передача размера единицы массы 1 кг граммовому набору гирь КГ-1-1110 (500, 200, 200, 100, 50, 20, 20, 10, 5, 2, 2 и 1 г).
Пример 2 Передача размера единицы массы 1 кг граммовому набору гирь КГ-1-1110 (500, 200, 200, 100, 50, 20, 20, 10, 5, 2, 2 и 1 г).
Ø  Пусть
Пусть
– значения масс гирь;
Ø  – значение массы эталона;
– значение массы эталона;
Ø 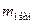 – значение массы вспомогательной гири 1 г
– значение массы вспомогательной гири 1 г
(из другого набора)
Ø Примечание
Ø  Измерения и расчёты производятся аналогично примеру 1.
Измерения и расчёты производятся аналогично примеру 1.
 |
Ø  Из уравнения (2) системы получим:
Из уравнения (2) системы получим:
 |
Ø Подставляя в уравнение (1), получим:
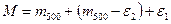 | |||
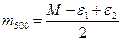 |
Ø Откуда
Ø 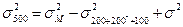 Определим СКО массы гири 500 г при известных СКО эталона и СКО устройства сравнения (компаратора):
Определим СКО массы гири 500 г при известных СКО эталона и СКО устройства сравнения (компаратора):
 | |||
 |
Ø Откуда
Ø  Из уравнения (5) системы получим:
Из уравнения (5) системы получим:
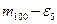 |
Ø  Подставляя в уравнения (3) и (4), получим:
Подставляя в уравнения (3) и (4), получим:
 |
Ø 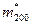

 Откуда или
Откуда или
Ø 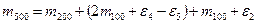 Подставляя в уравнение (2), получим:
Подставляя в уравнение (2), получим:
 | |||
 |
Ø  Подставляя в уравнение (2), получим:
Подставляя в уравнение (2), получим:
 |
Ø  Откуда
Откуда
По аналогии
 | |||
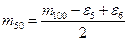 |
Ø  и т.д.
и т.д.
Ø При этом
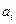 |
Ø 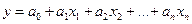 Задача – найти значения коэффициентов
Задача – найти значения коэффициентов
уравнения из эксперимента,
Ø в котором получены совокупности результатов измерений
Ø  Получим систему уравнений:
Получим систему уравнений:
Ø 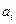 Если m = n, то система уравнений решается однозначно,
Если m = n, то система уравнений решается однозначно,
но из-за случайности в результатах измерений
при подстановке в неё других результатов того же эксперимента будут получаться другие значения
Ø 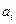 Если m > n, получим систему условных уравнений
Если m > n, получим систему условных уравнений
Ø  Предположим, что каким-то способом найдены
Предположим, что каким-то способом найдены
Ø 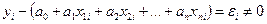 При подстановке в уравнения получим
При подстановке в уравнения получим
Ø Оценки коэффициентов находят из условия
 |
Ø для выполнения которого необходимо, чтобы
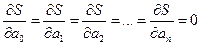 |
Ø Откуда

Ø Откуда
 |
Ø В обозначениях Гаусса:
 |  |
Ø получим:
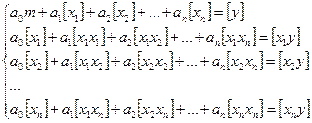 | |||
 |
Ø В результате:
 |  |
Ø  Оценки дисперсий коэффициентов:
Оценки дисперсий коэффициентов:
Ø  где D 00, D 11, D 22, …, Dnn – алгебраические дополнения элементов определителя D (получаются путём удаления из матрицы определителя D строки и столбца,
где D 00, D 11, D 22, …, Dnn – алгебраические дополнения элементов определителя D (получаются путём удаления из матрицы определителя D строки и столбца,
на пересечении которых находится данный элемент).
Ø 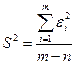 – оценка дисперсии условных уравнений
– оценка дисперсии условных уравнений
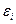 |
Ø – невязка условного уравнения
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 388; Нарушение авторских прав?; Мы поможем в написании вашей работы!