Квантова теорія фотоефекту

Другий і третій закони зовнішнього фотоефекту не вдається витлумачити на підставі класичної електромагнітної теорії світла. Згідно з цією теорією виривання електронів провідності з металів є наслідком їх „розгойдування” в електромагнітному полі світлової хвилі, яке повинне підсилюватись при зростанні інтенсивності світла і пропорційної її енергетичної освітленості фотокатода.

Ейнштейн, в продовж ідеї Планка про квантовану енергію атомів – осциляторів, висловив гіпотезу, згідно якої світло не тільки випромінюється, але і розповсюджується в просторі і поглинається речовиною у вигляді дискретних квантів електромагнітного випромінювання – фотонів.

При зовнішньому фотоефекті електрон провідності металів поглинає фотон, одержує його енергію 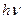повністю. Для виходу з металу електрон повинен здійснити роботу виходу А. Тому рівняння Ейнштейна для зовнішнього фотоефекту, яке виражає закон збереження енергії при фотоефекті, має вигляд:

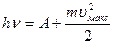(1.2)

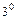З рівняння Ейнштейна безпосередньо випливає другий закон фотоефекту:

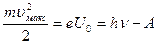(1.3)

Таким чином, 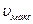і залежать тільки від частоти світла і роботи виходу електрона з фотокатода.

Максимальна початкова кінетична енергія фотоелектронів залежить від частоти світла по лінійному закону. Вона перетворюється в нуль при частоті , яка відповідає червоній границі зовнішнього фотоефекту:

(1.4)

Отже, червона границя залежить тільки від роботи виходу електрона з металу.

На рис. 1.4 зображена залежність максимальної кінетичної енергії фотоелектронів від частоти світла для цинку і нікелю. Усі прямі паралельні один одному, причому похідна не залежить від матеріалу катода й чисельно рівна постійної Планка h. Відрізки, що відсікаються на осі ординат, чисельно дорівнюють роботі А виходу електронів з відповідних металів.

При дуже великій інтенсивності світла спостерігається багатофотонний фотоефект: електрон може одночасно отримати енергію не одного, а N фотонів. У цьому випадку рівняння закону збереження енергії при зовнішньому фотоефекті під дією світла частоти має вигляд:

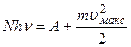(1.5)

Червона границя N – фотонного фотоефекту .

Зовнішній фотоефект – безінерційний, тобто випускання фотоелектронів починається одразу ж як тільки на фотокатод падає світло з частотою . Це є ще одне підтвердження квантового характеру взаємодії світла з речовиною.

6⁰ Основні закономірності зовнішнього фотоефекту для металів добре описуються теорією Фаулера. Згодне їй, після поглинання в металі фотона, його енергія переходить електронам провідності, внаслідок чого електронний газ в металі складається з суміші газів з нормальним розподілом Фермі-Дираку і збудженим (зрушеним на hν) розподілом по енергіях. Густина фотоструму визначається формулою Фаулера:

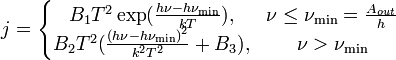
де B ₁, B ₂, B ₃ – постійні коефіцієнти, залежні від властивостей опромінюваного металу.

7. Як показали експерименти в національному метрологічному інституті Німеччини Physikalisch-Technische Bundesanstalt, результати яких опубліковані 24 квітня 2009 р. в Physical Review Letters, в м'якому рентгенівському діапазоні довжин хвиль при густині потужності на рівні декількох петаватт (10¹⁵ Вт) на квадратний сантиметр загальноприйнята теоретична модель фотоефекту може виявитися невірною. Відповідно до законів традиційного фотоефекту фотон, що володіє достатньо високою енергією, «вибиває» з атома один електрон із зовнішньої орбіти. Процес цей, як відомо, демонструє і підтверджує квантову природу світла. Відомо також, що при дуже високих інтенсивностях короткоімпульсного (фемтосекунди) довгохвильового випромінювання може відбуватися багатофотонна іонізація.

Порівняльні кількісні дослідження різних матеріалів в Гамбурзі показали, що глибина взаємодії між випромінюванням і речовиною істотно залежить від структури атомів цієї речовини і кореляції між внутрішніми електронними оболонками. У випадку з ксеноном, який використовувався в експериментах, дія пакету фотонів в короткому імпульсі приводить, до одночасної емісії безлічі електронів з внутрішніх оболонок.

Рис.1.5. Фотоіонізація ксенону: а) класичний фотоефект на зовнішніх рівнях при низькій інтенсивності фотонів; b) іонізація могутнім довгохвильовим випромінюванням; с) іонізація короткохвильовим рентгенівським випромінюванням високої інтенсивності.

§. Задача 1. Визначити максимальну швидкість υ _max фотоелектронів, що вилітають з поверхні срібла під дією:

1) ультрафіолетового випромінювання, довжина хвилі якого λ₁ = 155 нм;

2) γ – випромінювання з довжиною хвилі λ₂ = 2,47 нм.

Розв’язання. Максимальну швидкість фотоелектронів визначаємо з рівняння Ейнштейна для фотоефекту (2.3):

ε = А + Т _max. Енергію фотона визначаємо за формулою ε = hc /λ, роботу виходу А беремо з таблиць; для срібла А = 4,7 еВ.

Кінетична енергія фотоелектрона в залежності від того, яку він має швидкість, може бути виражена або за класичною формулою Т = m ₀ υ ²/2, або за релятивістською формулою Т = (m – m ₀) c ².

Швидкість фотоелектрона залежить від енергії фотона, який викликає фотоефект: якщо енергія фотона ε набагато менша від енергії спокою електрона m ₀ c ², то може бути застосована класична формула, якщо ε можна порівняти із величиною енергії спокою електрона, то в цьому випадку кінетичну енергію треба визначати за релятивістською формулою.

1. У формулу енергії фотона ε = h c/λ підставимо значення величин h, c, λ та, виконавши розрахунок, для ультрафіолетового випромінювання отримаємо ε₁ = 1,28 ∙10^-18 Дж = 8 еВ.

Це значення енергії фотона набагато менше енергії спокою електрона (0,51 МеВ). Тому для даного випадку максимальна кінетична енергія фотоелектрона може бути виражена за класичною формулою, а саме:

ε₁ = А + m ₀ υ ²_max/2, звідки υ _max = (2(ε₁ – A)/ m ₀ )^1/2. Підставивши числові значення А = 4,7 еВ = 0,75∙10^-18 Дж та m ₀ = 9,1∙10^{-31 кг, розраховуємо максимальну швидкість:} υ _max = 1,08∙10⁶м/с.

2. Енергія фотона γ-випромінювання дорівнює:

ε₂ = hc /λ₂ = 8,04∙10^-15 Дж = 0,502 МеВ.

Робота виходу електрона (А = 4,7 еВ) мала порівняно із енергією γ-фотона, тому максимальна кінетична енергія електрона практично дорівнює енергії фотона: Т _max = ε₂ = 0,502 МеВ.

Оскільки в даному випадку кінетичну енергія електрона можна порівняти із його енергією спокою, то для визначення швидкості електрона треба взяти релятивістську формулу для кінетичної енергії:

Т _max = m ₀ c ²(1/(1- υ ²_max/ c ²)^1/2 – 1)

Виконавши перетворення, визначаємо максимальну швидкість фотоелектронів: υ _max = 226∙10⁶м/с.

§. Задача 2. Фотон з енергією ε = 0,75 МеВ розсіюється на вільному електроні під кутом φ = 60⁰. Вважаючи, що кінетична енергія та імпульс електрона до вдаємодії з фотоном були нехтовно малими, визначити:

1) енергію ε ΄ фотона, що розсіюється, 2) кінетичну енергію електрона віддачі; 3) напрямок руху електрона.

Розв`язання. 1. Енергію фотона, що розсіюється, визначаємо з формули Комптона:

λ – λ ₀ = h (1 - cos φ)/ m ₀ c.

Виражаємо довжини хвиль λ і λ ₀ через енергії відповідних фотонів, тоді отримаємо:

hc / ε ΄ - hc / ε = h (1- cos φ)/ m ₀ c.

Поділимо обидві частини цього рівняння на hc, тоді:

1/ε΄ - 1/ε = (1- cos φ)/ m ₀ c ².

З останнього рівняння визначаємо енергію ε΄

ε΄ = ε / [(ε/ m₀c ²)(1- cos φ) + 1]. (1)

Виконавши числові розрахунки, отримаємо:

ε΄ = 0,43 МеВ.

2. Кінетична енергія електрона віддачі, як це випливає із закону збереження енергії, дорівнює різниці між енергією ε фотона, що падає, і енергією ε ΄ фотона, який розсіюється:

Е_К = ε - ε΄ = 0,32 МеВ.

3. Напрямок руху електрона віддачі визначаємо з закону збереження імпульсу, згідно якого імпульс р фотона, що падає, дорівнює векторній сумі імпульсу m₀ υ електрона віддачі та імпульсу р ΄ фотона, який розсіюється,:

p = p ΄ + m ₀ υ.

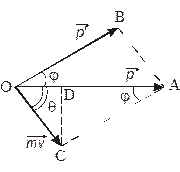Векторна діаграма імпульсів зображена на рис. 1.

Всі вектори на рис.1 проведені з точки О, де знаходився електрон у момент взаємодії з фотоном. Кут θ визначає напрямок руху електрона віддачі.

Із трикутника ОСD визначаємо:

tg θ = СD / ОD = CA ∙sin φ /(OA – CA ∙cos φ),

tg θ = p ΄ sin φ /(p - p ΄∙ cos φ).

Оскільки р = ε / c p ΄= ε΄/ c

tg θ = ε ΄∙ sin φ /(ε - ε ΄ cosφ). (2)

Перетворюємо формулу (2) так, щоб кут θ був виражений через величини φ і ε, які задані в умові задачі. З формули (1) маємо:

ε/ε ΄ = [ ε / E ₀(1- cos φ)] + 1. (3)

Виділивши у формулі (2) відношення ε/ε ΄ та замінивши його по формулі (3), отримаємо:

tg θ = sin θ /[(1+ ε / E ₀)∙(1- cos θ)].

Враховуючи, що sin θ = 2 sin (θ/2)∙ cos (θ/2) і (1- соs θ) = 2 sin ²(θ/2), після відповідних перетворень отримаємо:

tg θ = ctg (θ /2)/(1+ ε / E ₀).

Після числових розрахунків маємо tg θ = 0,701; звідки θ = 35⁰.

Відповідь: ε΄ = 0,43 МеВ, Е_к = 0,32 МеВ, θ = 35⁰.

§ .Корпускулярно-хвильовий дуалізм. Властивості хвиль де Бройля. Співвідношення невизначеностей Гейзенберга.

Інтерференція і дифракція світла переконливо свідчать про хвильову природу світла. У той же час закономірності рівноважного теплового випромінювання, фотоефекту й ефекту Комптона можна успішно витлумачити лише на підставі квантових уявлень про світло як про потік дискретних фотонів. Проте хвильовий і квантовий (корпускулярний) засіб опису світла не суперечать, а взаємно доповнюють один одного, так що світло одночасно володіє і хвильовими і корпускулярними властивостями. Воно є діалектичною єдністю (двоєдністю) цих протилежних властивостей.

Ідея універсальної корпускулярно-хвильової двоєдності стала основоположною в квантовій механіці.Квантова механіка виникла у зв’язку з потребою пояснити ті явища, які відбуваються в малих ділянках простору за участю частинок малої маси, тобто явища, які класична фізика пояснити була безсила. У 1924 р. Л. де Бройль висунув сміливу гіпотезу про корпускулярно-хвильовий дуалізм матеріальних частинок, основна ідея якої про хвильові властивості частинок була незабаром підтверджена на дифракції електронів, а потім – нейтронів, протонів, а також атомах гелію і натрію.

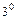У відповідності до теорії відносності Луі де Бройль виходить з припущення, що з кожною частинкою з масою спокою 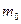пов’язаний хвильовий процес з частотою , так що , де h – стала Планка; с – швидкість світла у вакуумі. Цей основний постулат означає, що кожна частинка матерії є місцем і джерелом зв’язаного з нею коливання з частотою, яка визначається вищезгаданим співвідношенням. Тому формула де Бройля встановлює залежність довжини хвилі частинки, яка рухається, від імпульсу частинки p:

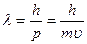, (1.1)

де m – маса частинки; 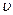– швидкість; h – стала Планка.

Ці хвилі називаютьсяхвилями де Бройля. Формули де Бройля мають також інший вигляд

, (1.2)

де – хвильовий вектор; а 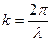– хвильове число, тобто число довжин хвиль, які укладаються на одиницях довжини, Дж×с.

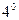Довжина хвилі де Бройля для частинки з масою m, яка має кінетичну енергію

(1.3)

Для електрона, який прискорився в електричному полі з різницею потенціалів вольт

. (1.4)

Хвильові властивості не виявлені у макроскопічних тілах. Довжини хвиль де Бройля для таких тіл настільки малі, що виявити хвильові властивості неможливо.

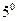Фазова швидкість хвиль де Бройля вільної частинки

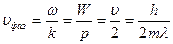, (1.5)

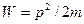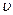де – енергія вільної частинки; – імпульс; m – маса; – швидкість частинки; 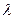– довжина дебройлевської хвилі. Залежність фазової швидкості дебройлевських хвиль від довжини хвилі показує, що хвилі зазнають дисперсії. Групова швидкість хвиль де Бройля дорівнює швидкості частинки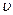

. (1.6)

Дата добавления: 2014-01-07