Приклади розвязувння задач

Розв’язуючи задачу з фізики, ми в першу чергу повинні за її змістом бачити фізичне явище, а потім для опису цього явища застосувати відповідні закони та формули. Тому ілюстрацією саме такого підходу до розв’язування фізичних задач будуть всі наступні приклади.

1.Задачі на рівномірний рух

Тіло приймає участь в незалежних рівномірних прямолінійних рухах, швидкості яких напрямлені по одній прямій.

Напевне, всі пам’ятають відому шкільну задачу з фізики такого змісту:

1. Ескалатор метро піднімає нерухомого пасажира за 1 хвилину. Ідучи вверх по нерухомому ескалатору пасажир підніметься за 3 хвилини. Питання - за який час підніметься пасажир, ідучи вверх по рухомому ескалатору?

Якщо запитати учня, чи навіть студента, про що йде мова в задачі, то майже всі скажуть – як про що, про ескалатор. А який же фізичний зміст задачі, які фізичні явища тут мають місце? А чи не подібна ця конкретна умова задачі до іншої, де замість рухомої стрічки ескалатора буде течія річки, яка несе нерухомий човен з 1 хвилину і човна, що рухається в стоячій воді, пропливає таку саму відстань за 3 хвилини. Питається, за який час човен, рухаючись з такою самою швидкістю відносно води, пропливе цю відстань за течією річки. Можна навести інші приклади подібних задач типу – літак летить в безвітряну погоду а потім за вітром і т.п. Але фізичний зміст таких задач однаковий: тіло, рухаючись рівномірно з деякою швидкістю v₁ проходить шлях S за час t_, .а рухаючись з швидкістю v₂ затрачає час t_2.. Який буде час руху t_3, коли швидкості додаються. Тому для даної задачі про рух людини по ескалатору метро або про рух човна скорочена умова матиме вигляд

Зрозумівши фізичну суть задачі, стає зрозумілим її математичне розв’язування, яке зводиться до системи трьох рівнянь, що описують ці рівномірні рухи:

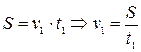
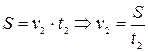
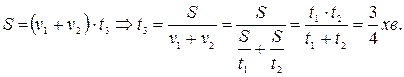
Тіло бере участь в двох рівномірних рухах, швидкості які перпендикулярні

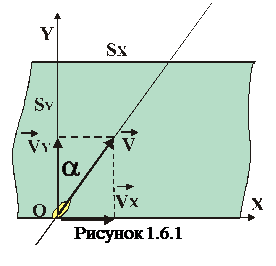
Тут конкретні умови задач можуть бути досить різні, наприклад, човен рухається перпендикулярно течії річки і течія зносить човен, літак летить на північ, дме західний вітер, куля пробиває вагон, що рухаються, – вхідний і вихідний отвори зміщені і т.п. Фізичний зміст таких задач однаковий, а саме: у вибраній системі відліку тіло вздовж вісі OX тіло рухається рівномірно з швидкістю v_x а вздовж вісі OY з швидкістю v_y. За час t тіло вздовж вісі OX пройде відстань, рівну 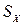, а вздовж вісі OY відстань 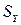. Результуюча швидкість v складає з віссю OY кут α. (рис.1.6.1.1).

Отже, рівняння кінематики такого руху матимуть такий вигляд:

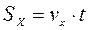- рівняння рівномірного руху вздовж вісі OX

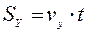- рівняння рівномірного руху вздовж вісі OY

- модуль результуючої швидкості

Цей кут 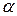називають відхиленням від курсу

Застосуємо ці рівняння до наступної задачі.

2.Поїзд їде рівномірно з швидкістю 52 км/год. Краплі дощу, які падають вертикально вниз, залишають на бічному склі вікна вагону косі сліди під кутом 70⁰ до вертикалі (рис.1.6.1). Визначити швидкість крапель дощу.

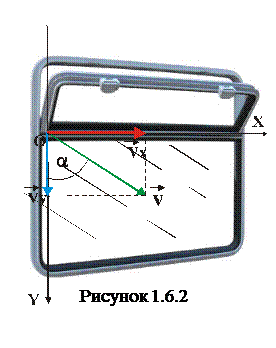
Якщо вибрати систему відліку, зв’язану з вагоном, спрямувавши вісь OX паралельно руху вагона, а вісь OY перпендикулярно, то відносно вагона краплі дощу приймають участь в двох незалежних прямолінійних рухах, швидкості яких перпендикулярні. Слід на вікні вагона вказує напрям вектора результуючої швидкості. Отже, скорочена умова задачі запишеться у вигляді:

Використавши співвідношення

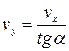отримаємо

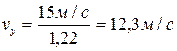
Якщо швидкості двох рухів складають довільний кут α, як вказано на рис 1.4.1.3, то результуюча швидкість v визначається за теоремою косинусів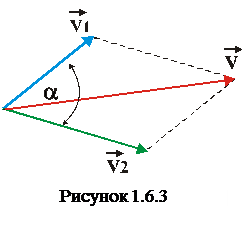

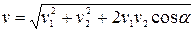
Наприклад, така відома задача про знаходження швидкості точки перетину двох прямих:

3. Одна пряма рухається паралельно сама собі з швидкістю v_1, а друга – зі швидкістю v_2.. Питання: з якою швидкістю v₃ рухається точка перетину цих прямих?

Cкорочену умову такої задачі доцільно записати у вигляді:

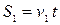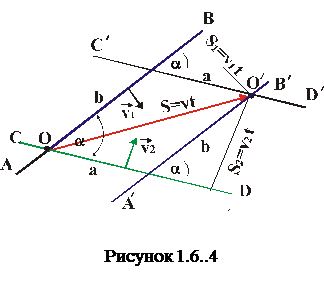
Розв’язок задачі стає зрозумілим, розглянувши рисунок 1.6.4 такого переміщення. Так, за довільний час t перша пряма зміститися на відстань , а друга на відстань. Тоді за цей час t точка перетину прямих пройде шлях 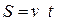– це фізика. А тепер починається елементарна математика.

Так, з рис.1.6.1.4 Бачимо, що відстань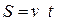є діагоналлю паралелограма зі сторонами a, b. Тому, застосувавши теорему косинусів, можна записати

.

З відповідних прямокутних трикутників знаходимо значення a та b

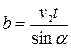
Підставивши ці значення в …., отримаємо

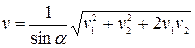
Якщо прямі рухаються з однаковими швидкостями v₁=v₂=v, то швидкість v₀ руху точки перетину цих прямих згідно з формулою ….буде рівна:

.

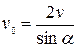Проаналізуємо отриманий результат. Так, якщо , то, тобто можна отримати як завгодно великі швидкості. Наприклад, дві прямі, кут між якими складає 0,0001 радіан, рухаються з однаковими швидкостями 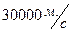, як вказано на рис.1.6.4. Тоді точка перетину цих двох прямих рухається зі швидкістю

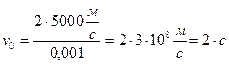
Тобто, у принципі, в майже у домашніх умовах можна отримати швидкість, яка перевищує швидкість світла у два рази.

На перший погляд отриманий результат ніби суперечить теорії відносності Ейнштейна, згідно з якою швидкість світла є максимально можливою швидкістю. Дійсно, швидкість світла – це максимальна швидкість руху матеріальних об’єктів, але в нашому прикладі з швидкістю 2с рухається всього лише геометрична точка перетину, а не тіло. Нагадаємо, що поняття точки, прямої та площини в геометрії не даються – це є абстрактні поняття. А що стосується надвеликих швидкостей, то поки що, як у відомій казці: питають, що на світі найшвидше. Відповідь: найшвидша – думка. Дійсно, думкою ми можемо миттєво здолати будь-які відстані.

2.Задачі на рівно змінний рух

Задачі першого рівня складності особливих труднощів не викликають. Тут рівноприскорений чи рівносповільнений рух легко описати відповідними елементарними формулами, які наведені на сторінці…. Наприклад:

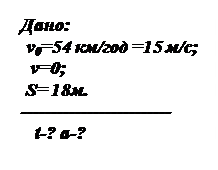1. Автомобіль проходить гальмівний шлях 20 м. Визначити час руху автомобіля до зупинки та модуль прискорення, якщо початкова швидкість 54 км/.

Так як рух рівносповільнений, то використовуючи формули цього руху, отримаємо

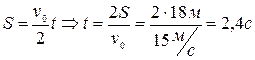
Деякі труднощі викликають задачі, в яких, на перший погляд, ніби відсутні звичні конкретні цифрові дані.

2. У скільки разів швидкість кулі при вильоті з ствола гвинтівки більша, ніж швидкість посередині ствола. Рух вважати рівноприскореним.

Як записати скорочено умову такої задачі? Дуже просто: довжина ствола – це шлях S₂, на якому тіло (в даному випадку куля) набуває швидкості v_2, а S₁- половина шляху S₂ (половина довжини ствола). Необхідно порівняти швидкості, яких набуває тіло на різних ділянках шляху, рухаючись зі стану спокою з однаковим прискоренням.

Для розв’язування задачі необхідні формули, які встановлюють зв’язок між шляхом та швидкістю рівноприскореного руху

Вільне падіння – це теж рівнозмінний рух, тільки у рівняннях такого руху замість шляху S записуємо висоту h, а прискорення – це прискорення вільного падіння g.

3. Град, падаючи з хмари за останню секунду свого падіння пролітає шлях, що становить 0,19 всієї висоти. Визначити час падіння та висоту, з якає падає град. Опором повітря нехтувати.

Звичайно, тут необхідна формула вільного падіння, але як в цю формулу ввести останню секунду і те, що протягом цієї останньої секунди пройдено 0,19 всього шляху (висоти). Тут доцільно зробити рисунок, який ілюструє таке падіння, і, по суті, цей рисунок буде коротким записом і майже готовим розв’язком задачі (рис1.6.5).

Рівняння 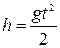описує вільне падіння зі всієї висоти за весь час падіння, а рівняння 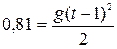стосується вільного падіння з висоти за час, менший на 1 секунду від загального часу t. Розділивши друге рівняння на перше, отримаємо

.

Беручи прискорення вільного падіння 10 м⁄с², висота, з якої падає град дорівнює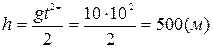

Наявність опору повітря суттєво впливає на падіння тіл

3 Рух тіла, кинутого горизонтально

Всі попередні задачі стосувались окремо рівномірного або рівнозмінного рухів. А що буде, коли тіло приймає участь в двох рухах – один з яких є рівномірним, а другий рівнозмінним. Прикладом такого руху є рух тіла, кинутого горизонтально. Тому розглянемо загальну задачу:

З висоти h в горизонтальному напрямі кинули тіло з швидкістю v_x. Описати кінематику такого руху

Тут можна виділити три рівня складності питань.

.

3 рівень: Визначити нормальне і тангенціальне прискорення тіла в будь якій точці траєкторії, а також її радіус кривизни в цій точці.

Перший рівень складності.

: Визначити час t руху, дальність S польоту тіла, швидкість v тіла в момент падіння на напрям швидкості – кут α між вектором швидкості і горизонтом Тіло вважати матеріальною точкою, опором повітря нехтувати.

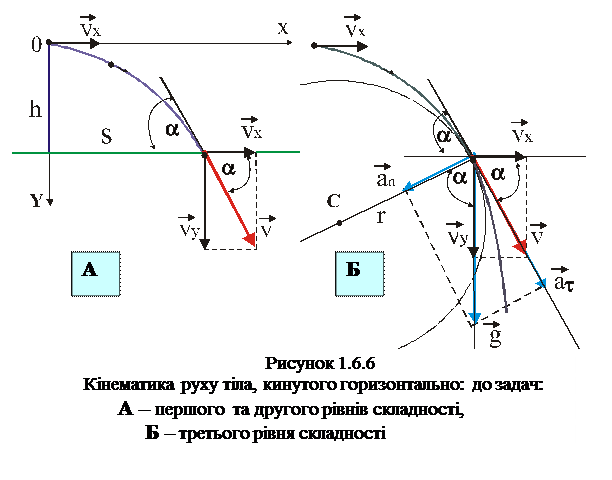
В даному випадку тіло приймає участь в двох незалежних рухах: рівномірний прямолінійний в горизонтальному напрямі з швидкістю v_x та вільне падіння з висоти h. (рис.1.6.6 А).

Тому ці рухи можна описати відповідними рівняннями, які відповідають розв’язку найпростішого першого рівня складності.

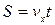– рівняння рівномірного руху, S – дальність польоту тіла, відстань по горизонталі від точки кидання до точки падіння.

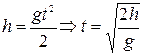– рівняння вільного падіння.

У даному русі горизонтальна швидкість v_x є сталою, змінюється швидкість v_y у вертикальному напрямі, як швидкість вільного падіння, тому

.

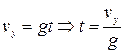Крім того, можна використати відомі співвідношення

.

Швидкість v, як вектор у будь якій точці траєкторії, є дотичним до траєкторії. З рисунка бачимо, що шукана швидкість v є результуючою швидкості v_x та v_y і модуль швидкості v дорівнює

.

Напрям швидкості визначається простим тригонометричним співвідношенням

.

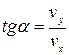Другий рівень складності

У вибраній системі відліку записати рівняння траєкторії руху тіла

Тут тілом відліку може бути дім, вежа, гора і т.п., звідки в горизонтальному напрямі кидають інше тіло. З тілом відліку зв’язуємо систему координат. У даному випадку найзручніше її початок вибрати в точці кидання, спрямувавши вісь X горизонтально, вісь Y вертикально вниз. Тоді рівняння рухів вздовж таких осей прийме вигляд:

,

звідки

,

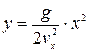тобто отримали рівняння параболи, крутизна якої визначається коефіцієнтом .

Третій рівень складності.

Визначити нормальне і тангенціальне прискорення тіла в будь якій точці траєкторії, а також її радіус кривизни в цій точці.

Цей рівень складності вимагає розуміння фізичного змісту понять нормального і тангенціального прискорень і чому саме в даному випадку руху тіла, кинутого горизонтально, ми зустрічаємось з такими прискореннями. З рис.1.6.6.Б бачимо,що вектор результуючої швидкості стає «довшим», отже, змінюється швидкість за модулем, тобто існує тангенціальне прискорення. Крім того, вектор результуючої швидкості змінює свій напрям, значить, присутнє нормальне прискорення. А що «розтягує» і «закручує» вектор швидкості? Звичайно, це все робить земне тяжіння, де всі тіла падають з однаковим прискоренням – прискоренням вільного падіння g. Отже, у нашому випадку повне прискорення – це прискорення вільного падіння. Рис.1.6.6 Б є, по суті, розв’язком визначення нормального та тангенціального прискорень у заданій точці. Вектор повного прискорення, тобто вектор прискорення вільного падіння, розкладаємо на дві складові: тангенціальне прискорення 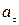, напрямлене по дотичній до траєкторії та нормальне , перпендикулярне до швидкості.

З подібності векторних трикутників швидкостей та прискорень маємо:

.

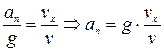Визначивши нормальне прискорення з співвідношення

,

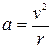легко визначити радіус кривизни траєкторії

.

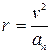На рис. радіус кривизни траєкторії в даній точці – це радіус кола, яке своєю елементарною дугою співпадає з елементарною дугою траєкторії.

Для прикладу, користуючись вище наведеними формулами, визначимо радіус траєкторії тіла в точці, яка відповідає положенню тіла, кинутого горизонтально зі швидкістю 10 м⁄с через 1 с руху. Через цей час швидкість тіла становитиме .

Отже, нормальне прискорення буде рівним

.

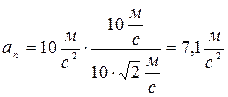Визначивши нормальне прискорення, легко підрахувати радіус кривизни траєкторії

.

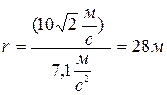Що стосується тангенціального прискорення, то

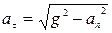
і через 1с воно буде становитиме

.

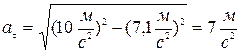До третього рівня складності про рух тіла, кинутого горизонтально, можна віднести задачі про кінематику одночасного руху декількох тіл.

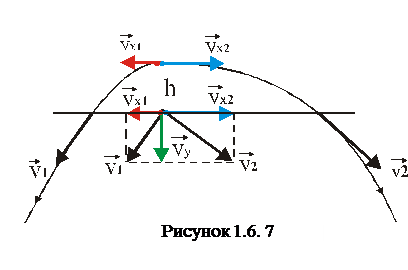
2. Із однієї точки вилітають дві частинки з горизонтально протилежними швидкостями v_1х =2м/с та v₂ =5 м/с. Через який час кут між напрямами швидкостей цих частинок стане рівним 90⁰?

Мова йде про результуючі швидкості v ₁ v ₂, які дотичні до траєкторії. Розв’язок задачі стане зрозумілим, якщо в одну точку перенести ці вектори, які згідно умови задачі перпендикулярні. (рис.1.6.7) Горизонтальні складові швидкостей залишаються сталими, а вертикальна складова v_y, як швидкість вільного падіння, , буде однаковою і ця швидкість, як вектор, є спільною висотою двох прямокутних трикутників, де гіпотенузами є швидкості 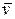та 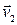і катетами , .

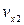Тому

.

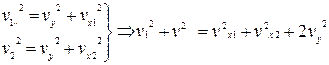З «великого» прямокутного трикутника, де гіпотенузою є сума отримаємо

.

Прирівнюючи два останніх рівняння і враховуючи, що 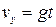, отримаємо

.

4 Рух тіла, кинутого під кутом до горизонту

Рух тіла, кинутого під кутом до горизонту можна уявити як два незалежних рухи. Так, якщо швидкість v _0, з якою кинули тіло під кутом α до горизонту, розкласти на дві складові: горизонтальну 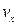та вертикальну , як вказано на рис 1.6.8, то тіло здійснює два наступні незалежні рухи:

1. Рівномірний прямолінійний в горизонтальному напрямі з швидкістю v _x

2. Рух тіла, кинутого вертикально вгору з швидкістю v_y0 – до верхньої точки рівносповільнений, а з верхньої точки вниз – рівноприскорений.

Тому задача першого рівня складності про рух тіла, кинутого під кутом горизонту має наступний зміст:

1. Тіло, кинуте зі швидкістю v₀ під кутом α до горизонту. Визначити максимальну висоту підняття тіла, час руху та дальність польоту тіла (відстань по горизонталі від точки кидання до точки падіння).

Тепер математично опишемо ці рухи:

1. Рівняння рівномірного руху

,

де S – дальність польоту тіла, відстань по горизонталі від точки кидання до точки падіння за час t.

Позначивши час всього руху t, час руху вгору до верхньої точки буде становити t/2 (такий самий час руху вниз). Використовуючи відомі співвідношення для вільного падіння, можна записати наступні рівняння, де h – максимальна висота підняття.

.

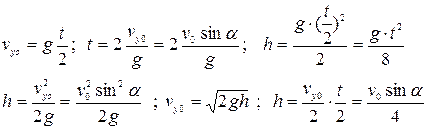
Використовуючи ці формули, легко розв’язати задачі першого рівня складності, де треба з цих формул визначити ту чи іншу величину. До другого рівня складності можна віднести задачі про визначення радіуса кривизни траєкторії у верхній точці та швидкості тіла у будь якій точці траєкторії. Тому на цих задачах доцільно зупинитись біль детально.

2. Тіло,кинутепідкутомдогоризонту з швидкістюv_0. Визначитирадіус r кривизни траєкторії у її верхній точці.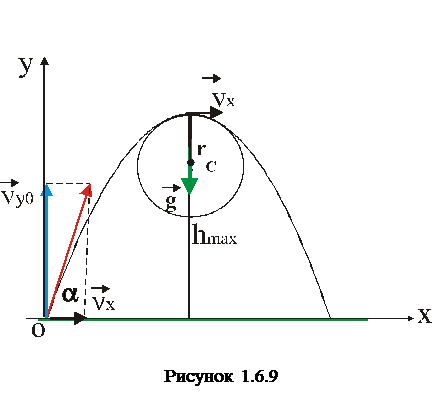

Типова помилка, яку допускають при розв’язку даної задачі полягає в тому, що радіусом кривизни траєкторії вважають максимальну висоту підняття тіла. Але зверніть увагу на рисунок – верхня частина траєкторії являє собою вершину параболи. В принципі, виключивши час з рівнянь руху по горизонталі та по вертикалі 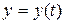(вісь У), можна отримати рівняння траєкторії і з цього рівняння можна визначити радіус кривизни кривої (параболи) в будь-якій точці. Але фізика дає простий розв’язок поставленої задачі. Ще раз зверніть увагу на точку у верхній частині траєкторії. У цій точці вектор прискорення вільного падіння 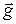перпендикулярний до вектора швидкості , отже прискорення вільного падіння у верхній точці траєкторії виконує роль нормального (доцентрового) прискорення. Тому

.

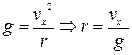В окремих випадках розв’язування навіть складних задач кінематики спрощується застосуванням закону збереження і перетворення енергії. Це стосується кінематики руху тіла, кинутого вертикально, горизонтально або під кутом до горизонту. Наприклад:

3. Тіло,кинутепідкутомдогоризонту з швидкістюv_0. Визначитишвидкістьтіланадовільнійвисоті у.

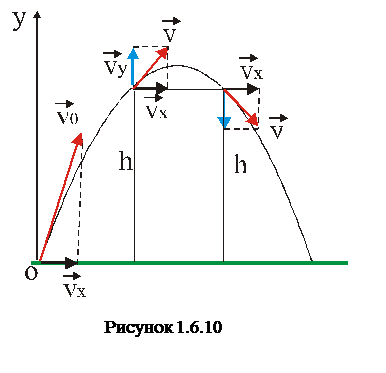
В умові задачі не вказаний кут кидання, тому, як кажуть в приказці, «обійдемо всі гострі кути», і за що тут можна «зачепитися» без кута, який не вказаний в умові. Є одна непогана ідея – невідома швидкість та відома є гіпотенузами прямокутних трикутників, в яких є однаковий катет v_x, а другий катет – швидкість у вертикальному напрямі, і ця швидкість зменшується з висотою. Отже, необхідно записати такі рівняння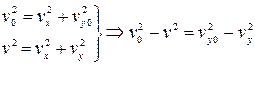

Так як 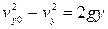(див. таблицю формул на ст….), то, відповідно, .

Тепер ця сама задача з точки зору збереження і перетворення енергії. А саме: якщо б тіло досягло максимальної висоти, то кінетична енергія тіла повістю перейшла би в потенціальну енергію. Але тут тіло не на максимальній висоті, воно володіє як кінетичною, так і потенціальною енергією, тому, згідно закону збереження та перетворення енергії, будемо мати

.

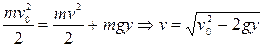Переконались – як просто без геометрії та формул кінематики знайдена шукана кінематична величина. Забігаючи наперед, відмітимо – застосування закону збереження і перетворення енергії є надзвичайно потужним методом опису процесів різної природи. В розділі «ДИНАМІКА» ми покажемо, що замість диференціального рівняння, яке описує зісковзування шнура зі столу досить застосувати елементарну формулу перетворення потенціальної енергії в кінетичну. Але щоб не склалось враження про можливість розв’язку таким способом абсолютно всіх задач, перейдемо до задачі третього рівня про рух тіла, кинутого під кутом до горизонту з нестандартними умовами, які вимагають теж нестандартного підходу до їх розв’язку. Тут не можна дати готових вказівок – застосування тієї чи іншої формули.

4. Із шланга, який лежить на землі, під кутом 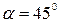б’є вода з початковою швидкістю 10 м/с. Площа перерізу отвору S=5 см². Визначити масу струменя води, яка перебуває в повітрі. Густина води 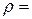1000 кг/м³.

Якщо б ми знали об’єм V струминю води, що знаходиться в повітрі, то маса цієї води дорівнювала би 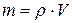. Питання – як знайти такий об’єм. В принципі, склавши рівняння траєкторії (це буде парабола з вершиною в найвищій точці), математично означеним інтегралом можна знайти її довжину. Але ми спробуємо, якщо нам вдасться, обійтись без вищої математики, добре подумавши – а звідкіля береться цей струмінь води? Для цього згадаємо дитячий водяний пістолет, який вистрілює струмінь води, тобто об’єм води, що був в пістолеті опиняється в повітрі. Так ось, роль такого вже не водяного пістолета, а, по суті, водяної гармати, буде виконувати шланг-труба, в якій переміщається зі швидкістю v поршень площею S. З цієї труби, нахиленої під кутом α до горизонту, б’є вода з такою ж швидкістю, з якою рухається поршень. Шланг, тобто труба, заповнені водою, струмінь поки що відсутній, пунктиром позначена майбутня траєкторія (рис 1.6.11 А). Далі при русі поршня траєкторія руху все більше заповнюється водою і коли запаси води в трубі закінчаться, як вказано на другій позиції рисунку 1.6.11 Б, вода буде в повітрі.

Отже, шуканий об’єм води дорівнює , де L – переміщення поршня, так що . А час t руху поршня і буде часом руху тіла, кинутого під кутом до горизонту, де в даному випадку таким тілом є струмінь води. Цей час, як вже було раніше вказано, дорівнює

.

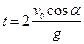Тому шукана маса води буде становити

,

а підставивши числові значення всіх величин отримаємо, що m=7,2 кг.

Розглянуті задачі про рух тіла, кинутого під кутом до горизонту стосувались того випадку, коли точка кидання та падіння знаходяться на одній горизонтальній прямій. Але можуть бути інші випадки. Тіло кидають з деякої висоти під кутом до горизонту вгору або вниз. Тому окремо розглянемо такі випадки.

5. Спортсменка штовхає ядро з висоти свого обличчя на висоті 165 см під кутом 45⁰ з швидкістю 12 м/с. Визначити дальність польоту ядра (відстань по горизонталі від точки кидання до точки падіння (хоча в спорті цю відстань відраховують від краю сектора для штовхання ядра).

.

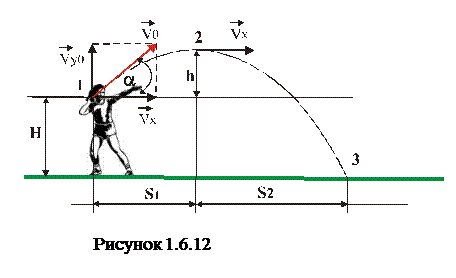
9. Тут зручно рух ядра розділити на дві частини (рис.1.6.12): 1) рух тіла, кинутого під кутом до горизонту, але рух лише до верхньої точки протягом часу t₁ і тіло ще піднімається на «додаткову» висоту h). 2) Рух тіла, кинутого горизонтально з висоти H+h і цей рух буде тривати час t₂ до падіння ядра на землю.

Визначивши принцип (ідею) розв’язку задачі справа лишається за технікою – скласти рівняння вказаних рухів.

1. Рух від точки 1 до 2.

.

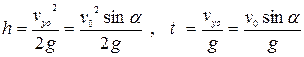2. Рух від точки 2 до 3.

.

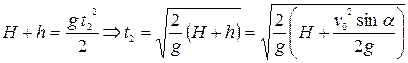Тоді дальність польоту становитиме

.

Підставивши числові значення, отримаємо S= 15,86 м. Найвищий результат по штовханню ядра серед жінок був встановлений у 2010 Надією Остапчук. Вона штовхнула ядро на 20,85м на зимовому чемпіонаті світу.

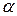З деякої висоти (балкона, вежі, з крутого берега ріки і т.п.) тіло можуть кидати під кутом до горизонту тільки не вгору, а вниз. Тому прикладом такого руху тіла, кинутого з висоти вниз зі швидкістю під кутом до горизонту буде наступна задача.

6. З літака, який летить на висоті 500 м з швидкістю 360 км/год під кутом 20⁰ до горизонту скидають вантаж. На якій відстані по горизонталі від точки падіння вантаж впаде на землю, якщо опором повітря знехтувати?

5. Якщо розкласти швидкість v на дві складові: v_x - горизонтальну та v_y -вертикальну ( рис.1.6.13), то вантаж приймає участь в двох незалежних рухах

1. Рівномірний прямолінійний в горизонтальному напрямі з швидкістю v_x

_.

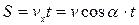2. Рух тіла, кинутого вертикально вниз з висоти h з початковою швидкістю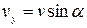

.

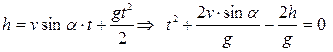Підставивши числові значення і розв’язавши таке квадратне рівняння, отримаємо: час руху становитиме t=7,2 c. Тоді, згідно першого рівняння, шукана відстань S буде мати наступне значення

.

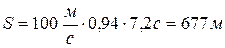5.Задачі на середню і миттєву швидкість та миттєве прискорення

В багатьох випадках рух тіла як матеріальної точки задається рівнянням залежності шляху від часу. Тоді швидкість іприскореннявизначаютьсяяквідповідніматематичніпохідні. Практично в усіх збірниках задач ви зустрінете подібну умову:

1. Залежність шляху S від часу tпри русі тіла задано рівнянням S=Вt+Сt²+Dt³, де В=10 м/с, С=6 м/с² та D=2 м/с³. Визначити шлях, швидкість та прискорення тіла через 4 с після початку руху.

1. Підставляємо час t = 4с та визначаємо шлях S=264м.

2. Швидкість – перша похідна від шляху по часу

.

3. Прискорення – перша похідна від швидкості по часу

.

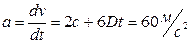Дійсно, задача дуже проста, навіть думати особливо не треба – є готові правила, треба лише вміти брати похідні. Але ми говорили і далі будемо говорити, що кожна задача з фізики описує відповідне фізичне явище. Тому проаналізуємо подане рівняння руху. По-перше – який цей рух, прямолінійний чи криволінійний. На це питання відповідь більш проста, ніж математика – а хто його знає. Може, тіло рухалось по колу або по сторонах трикутника або як завгодно, але в усіх випадках шлях, як скалярна величина той самий: S=264 м. Так само, отримана швидкість v=125м/с – це лише модуль швидкості, напрям невідомий. Але, крім того, в даному рівнянні руху є ще одна величина D=2м/с³, яка вказує на зміну самого прискорення. А чи можливий такий рух зі змінним прискоренням? Прикладом такого руху зі змінним прискоренням може бути рух автомобіля – більше тиснемо на «газ» більша сила тяги, більше прискорення.

В багатьох випадках важливою практичною задачею є визначення не миттєвої, а середньої швидкості. Дійсно, хто не знає автомобільних заторів у містах: швидкісні автомобілі, вистоюючи в заторах, ледве долають кілометр-другий хвилин за 20-30, а то і більше.

Для знаходження модуля середньої швидкості 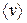необхідно розділити весь шлях S нерівномірного руху на той час t, за який цей шлях пройдено (навіть, враховуючи час, коли тіло не рухалось, наприклад, зупинки автомобіля).

.

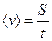Пропонуємо розглянуті вже відомі, так звані, класичні задачі на середню швидкість.

2. Першу половину часу автомобіль рухався з швидкістю 60 км/год, а другу половину часу з швидкістю 40 км/год. Визначити середню швидкість протягом всього часу.

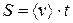- весь шлях S за час t з середньою швидкістю 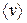--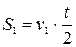 шлях за першу половину 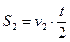, шлях за другу половину часу

Так як ,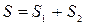

то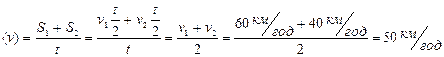

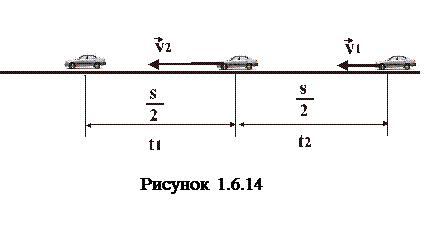А тепер дещо подібна задача, тільки різниця в тому, що:

3. Першу половину шляху автомобіль рухався з швидкістю 60 км/год, а другу половину шляху з швидкістю 40 км/год. Визначити середню швидкість протягом всього часу.

Тут доцільно зробити рисунок (1.6.14)., який, ілюструє розв’язок задачі

- весь шлях S за час t з середньою швидкістю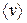

перша половинашляхуза час t₁, 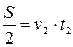- друга половина

шляху за час t_2.

Так як загальний час t дорівнює сумі , то середня швидкість буде дорівнювати

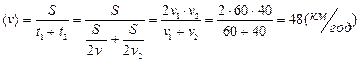
Задача з елементами інтегрального числення.

4.Залежність швидкості від часу при русі тіла, задано рівнянням , де А=6 м/с² і В=2 м/ с³ . Визначити середню швидкість тіла при його русі протягом часу від t₁= 2 с до t₂=10 c. В даному в випадку за час Δt=t₂- t₁ тіло пройде відстань ΔS=S₂–S₁ і середня швидкість знаходиться відношенням .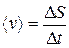

Наведена в умові задачі залежність швидкості від часу вказує на те, що при даному русі змінюється не тільки швидкість, але змінюється ще й прискорення (зверніть увагу на коефіцієнт В). Тому лише за нескінченно малий проміжок часу 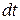рух можна вважати рівномірним з миттєвою швидкістю v і елементарний шлях 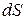, що пройде тіло за цей час буде дорівнювати , а весь шлях – інтегральній сумі

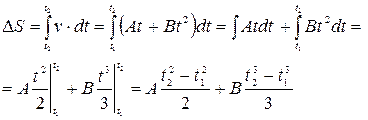
Підставивши числові значення величин, отримаємо

.

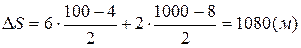І тоді середня швидкість буде становити .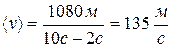

6.Задачі кінематики обертального руху

1. Колесо починає обертатись зі стану спокою і, зробивши 100 обертів, досягає кутової швидкості 62,8 рад/с. Вважаючи рух рівноприскореним, визначити час та кутове прискорення даного обертового руху.

В даному випадку найпростіше застосувати готові формули порівняння кінематики поступального та

обертового рухів, враховуючи, що роль шляху

при обертовому русі грає кут φ=2ΠN. Отже, замість 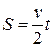запишемо 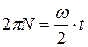. Аналогічно, замість виразу 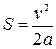будемо мати .

Підставляючи числові значення в розрахункові формули, отримуємо:

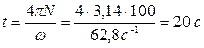
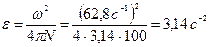
2. З якою лінійною швидкістю рухаються точки екватора Землі під час її обертання навколо власної осі? Радіус землі вважати R=6400 км.

За час, рівний періоду обертання Т, будь-яка точка екватора опише коло довжиною , і тоді лінійна швидкість точок екватора визначається співвідношенням

.

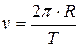Так як період обертання Землі становить 24 год., то

.

Це досить велика швидкість у масштабі швидкостей ракетної техніки, особливо при запуску штучних супутників Землі. Тому цю швидкість і використовують при запуску ракет, так як до швидкості ракети додається ще швидкість обертання Землі. Між Україною і Бразилією укладена угода про запуск з бразилійського космодрому «Алкантара» у районі екватора української ракети-носія «Циклон-4», старт якої показаний на рис.1.6.15

Ракети, які стартують з «Алкантари», використовують на 13% менше пального, ніж ті, що запускаються з мису Канаверал в США, та на 31% менше, ніж ракети, пуск яких здійснюється з космодрому «Байконур» у Казахстані.

3. Матеріальна точка рухається по колу радіусом 0,2 м і кінематичне рівняння обертового руху має вигляд , де А=3 рад/с, В=4 рад/с², С=2 рад/с³. Після початку руху пройшло 4 секунди. Необхідно визначити:

1. Скільки обертів N буде здійснено за цей час;

2. Кутову швидкість ω в цей момент;

3. Кутове прискорення ε;

4. Лінійну швидкість v;

5. Нормальне a_n та тангенціальне a_τ прискорення;

Дата добавления: 2014-01-07