Тема 4.2. Дифференциал функции одной переменной

Диференціал -го порядку визначається як.

Питання для самоконтролю:

1. Дайте означення диференціала функції

2. Сформулюйте правила знаходження диференціала функції

3. Як знайти диференціал складної функції?

4. Запишіть формулу для наближених обчислень значень функції.

Определение 4.2. Дифференциалом функции 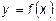называется главная часть ее приращения, линейная относительно приращения аргумента.

Определение 4.3. Дифференциалом аргумента называется приращение этого аргумента: .

Дифференциал функции определяется по формуле

Геометрический смысл дифференциала функции в точке 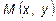: он численно равен приращению ординаты касательной к графику функции в этой точке.

Дифференциал функции используется, для приближенных вычислений:

.

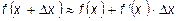Дифференциал 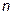-го порядка определяется как

.

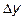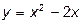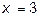Задача 4.5. Сравнить приращение и дифференциал функции при и .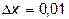

Дата добавления: 2014-01-07