Зростання та спадання функцій

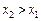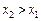Функція f (x) називається зростаючою на проміжку, якщо більшому значенню аргументу відповідає більше значення функції (якщо то ); функція спадна на проміжку, якщо більшому значенню аргументу відповідає менше значення функції (якщо , то ).

Теорема 1 (необхідна умова зростання (спадання) функції):

1. Якщо диференційована функція зростає на деякому проміжку, то похідна цієї функції невід’ємна на цьому проміжку.

2. Якщо диференційована функція спадає на деякому проміжку, то похідна цієї функції не додатна на цьому проміжку.

Теорема 2 (достатня умова зростання (спадання) функції):

1. Якщо похідна диференційованої функції додатна всере­дині деякого проміжку, то функція зростає на цьому проміжку.

2. Якщо похідна диференційованої функції від’ємна всере­дині проміжку, то функція спадає на цьому проміжку.

Приклад. Знайти проміжки зростання та спадання функції .

Область визначення функції — уся числова вісь .

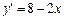
Функція диференційована на проміжку .

Для визначення проміжку зростання функції розв’яжемо нерівність 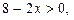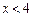, тобто функція зростає на проміжку .

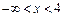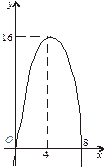
При визначенні проміжку спадання функції (рис. 1) маємо

8 – 2 х < 0, тобто 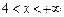. Рис.1

Дата добавления: 2014-01-07