Екстремуми функцій

Означення. При значенні х ₁ аргументу х функція f (х) має максимум f (х ₁), якщо в деякому околі точки х ₁ виконується нерівність (рис. 2) 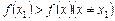. Аналогічно: при значенні х ₂ аргументу х функція f (х) має мінімум f (х ₂), якщо в деякому околі точки х ₂ має місце нерівність (рис. 2) .

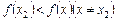Рис. 2

Максимум або мінімум функції називається екстремумом функції, а ті значення аргументу, при яких досягаються екстремуми функції, називаються точками екстремуму функції (відповідно точками максимуму або мінімуму функції).

Екстремум функції, у загальному випадку, має локальний характер — це найбільше або найменше значення функції порівняно з ближніми її значеннями.

Необхідна умова екстремуму функції. Теорема. У точці екстремуму диференційовної функції похідна її дорівнює нулю:

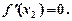(1)

Геометрична умова (1) означає, що в точці екстремуму диференційованої функції 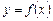дотична до її графіка паралельна осі Ох (рис. 3).

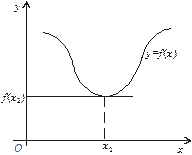
Рис. 3

Наслідок. Неперервна функція може мати екстремум тільки в тих точках, де похідна функції дорівнює нулю або не існує.

Справді, якщо в точці х ₀ екстремуму функції 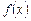існує похідна 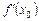, то, згідно з даною теоремою, ця похідна дорівнює нулю.

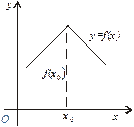Рис. 4

Те, що в точці екстремуму неперервної функції похідна може не існувати, показує приклад функції, графік якої має форму «ламаної» (рис. 4).

Ті значення аргументу х, які для заданої функції перетворюють на нуль її похідну 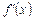або для якої похідна 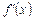не існує (наприклад, перетворюється на нескінченність), називаються критичними значеннями аргументу (критичними точками).

Достатні умови екстремуму функції. Із того, що 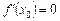, не випливає, що функція 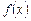має екстремум при .

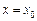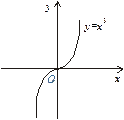Рис. 5

Наприклад, нехай 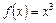. Тод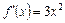і і 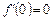, однак значення 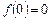не є екстремумом даної функції, оскільки різниця 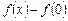змінює знак при зміні знаку аргументу х (рис. 5).

Отже, не для будь-якого критичного значення аргументу функції 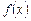має місце екстремум цієї функції. Через це поряд з необхідною умовою існують достатні умови існу­вання екстремуму функції.

Дата добавления: 2014-01-07