
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема 1 (перше правило)
|
|
|
|
Нехай функція 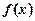 неперервна на деякому інтервалі, в якому міститься критична точка х 0, і диференційована в усіх точках цього інтервалу (крім, можливо, самої точки х 0). Якщо при переході зліва направо через цю точку похідна:
неперервна на деякому інтервалі, в якому міститься критична точка х 0, і диференційована в усіх точках цього інтервалу (крім, можливо, самої точки х 0). Якщо при переході зліва направо через цю точку похідна:
1) змінює знак з «+» на «–», то при х = х 0 функція має максимум;
2) змінює знак «–» на «+», то функція має у цій точці мінімум;
3) не змінює свого знака, то функція в точці х = х 0 екстремуму не має.
Геометрична ілюстрація теореми 1 (рис. 6). Нехай у точці х = х 1 маємо  і для всіх х, достатньо близьких до точки х 1, виконуються нерівності
і для всіх х, достатньо близьких до точки х 1, виконуються нерівності

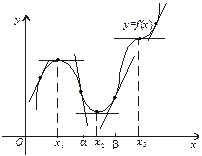
Рис. 6
Тоді при  дотична до кривої утворює з віссю Ох гострий кут — функція зростає, а при
дотична до кривої утворює з віссю Ох гострий кут — функція зростає, а при  дотична утворює з віссю Ох тупий кут — функція спадає; при х = х 1 функція переходить від зростання до спадання, тобто має максимум.
дотична утворює з віссю Ох тупий кут — функція спадає; при х = х 1 функція переходить від зростання до спадання, тобто має максимум.
Якщо в точці х 2 маємо 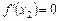 і для всіх значень х, достатньо близьких до точки х 2, виконуються нерівності
і для всіх значень х, достатньо близьких до точки х 2, виконуються нерівності

то при  дотична до кривої утворює з віссю Ох тупий кут — функція спадає, а при
дотична до кривої утворює з віссю Ох тупий кут — функція спадає, а при 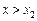 дотична до кривої утворює гострий кут — функція зростає. При х = х 2 функція переходить від спадання до зростання, тобто має мінімум.
дотична до кривої утворює гострий кут — функція зростає. При х = х 2 функція переходить від спадання до зростання, тобто має мінімум.
Якщо при х = х 3 маємо  і для всіх значень х, достатньо близьких до х 3, виконуються нерівності
і для всіх значень х, достатньо близьких до х 3, виконуються нерівності 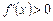 при
при 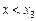 ;
; 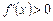 при
при 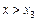 , то функція зростає як при
, то функція зростає як при 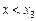 , так і при
, так і при 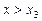 . Звідси при х = х 3 функція не має ні максимуму, ні мінімуму.
. Звідси при х = х 3 функція не має ні максимуму, ні мінімуму.
Зауваження. На основі даної теореми можна сформулювати таке правило для дослідження неперервної функції 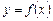 на максимум і мінімум.
на максимум і мінімум.
1. Знаходимо першу похідну функції, тобто 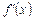 .
.
2. Обчислюємо критичні значення аргументу х (критичні точки), для цього:
а) прирівнюємо першу похідну до нуля і знаходимо дійсні корені здобутого рівняння 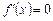 ;
;
б) знаходимо значення х, для яких похідна 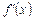 має розрив.
має розрив.
3. Досліджуємо знак похідної ліворуч і праворуч від критичної точки. Оскільки знак похідної залишається сталим в інтервалі між двома критичними точками, для дослідження знака похідної ліворуч і праворуч, наприклад від критичної точки х 2 (рис. 6), досить визначити знак похідної в точках  і
і 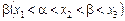 , де х 1 і х 3 — найближчі критичні точки).
, де х 1 і х 3 — найближчі критичні точки).
4. Обчислюємо значення функції 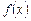 у кожній критичній точці.
у кожній критичній точці.
Приклад. Дослідити на максимум і мінімум функцію 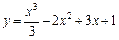 .
.
l 1. Знаходимо першу похідну 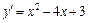 .
.
2. Знаходимо дійсні корені рівняння  . Звідки
. Звідки 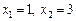 .
.
Похідна скрізь неперервна. Значить, інших критичних точок для заданої функції не існує.
3. Досліджуємо критичні значення. Для цього область визначення функції 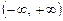 здобутими критичними точками розбиваємо на три інтервали
здобутими критичними точками розбиваємо на три інтервали 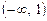 , (1, 3), (
, (1, 3), (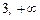 ).
).
Виберемо в кожному інтервалі по одній точці і обчислимо значення похідної в цих точках:
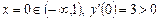 ;
;
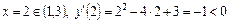 ;
;
 .
.
Знак похідної на кожному з трьох інтервалів збігається зі знаком похідної в обраній точці відповідного інтервалу (табл. 1).
З таблиці видно: при переході (зліва направо) через значення
х = 1 похідна змінює знак з «+» на «–». Звідси, при х = 1 функція має максимум:
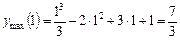 .
.
Таблиця 1
| х | (– ¥, 1) | (1, 3) | (3, + ¥) | ||
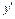
| + | – | + | ||
 у у
| 
| 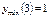
|
При переході через значення х = 3 похідна змінює знак з «–» на «+». Звідси, при х = 3 функція має мінімум:
 .
.
На інтервалі:
1) 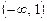 — функція зростає;
— функція зростає;
2) (1, 3) — спадає;
3) 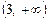 — зростає.
— зростає.
Крім того,
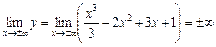 .
.
На основі проведеного дослідження будуємо графік функції (6).
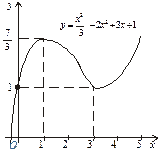
Рис. 6
Теорема 2 (друге правило). Якщо для диференційовної функції  у деякій точці х 0 її перша похідна
у деякій точці х 0 її перша похідна  дорівнює нулю, а друга похідна
дорівнює нулю, а друга похідна 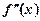 існує й відмінна від нуля, тобто
існує й відмінна від нуля, тобто 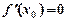 ,
,  , то:
, то:
1) якщо друга похідна  , то в точці х 0 функція
, то в точці х 0 функція 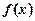 має мінімум;
має мінімум;
2) якщо 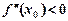 — максимум;
— максимум;
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 265; Нарушение авторских прав?; Мы поможем в написании вашей работы!