Алгоритм Фаррара-Глобера

Дослідити мультиколінеарність можна з допомогою алгоритму Фаррара-Глобера. Цей алгоритм має три види статистичних критеріїв, згідно з якими перевіряється: мультиколінеарність усього масиву факторів (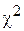); кожної незалежної змінної з рештою змінних (F-критерій); кожної пари незалежних змінних (t-критерій).

Усі ці критерії дають змогу робити конкретні висновки щодо наявності чи відсутності мультиколінеарності незалежних змінних.

Наведемо алгоритм Фарарра-Глобера

1. Визначення загальної мультиколінеарності

Для цього знаходиться визначник кореляційної матриці R і обчислюється розрахункове значення .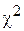

(7.23)

Значення цього критерію порівнюється з табличним при 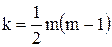ступенях вільності і заданому рівні ймовірності.

Якщо 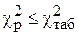, то із заданою надійністю можна вважати, що загальна мультиколінеарність відсутня і на цьому закінчується дослідження мультиколінеарності. Якщо 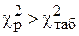, то з прийнятою надійністю можна вважати, що між факторами існує мультиколінеарність.

Для з’ясування питання, між якими факторами існує мультиколінеарність, використовується F- або t-статистика.

2. Обчислення матриці Z

Знайдемо матрицю, обернену до матриці R

.

3. Обчислення F-критеріїв

F-критерії для кожної пояснювальної змінної обчислимо за формулою

(7.24)

z_jj – діагональні елементи матриці Z.

Фактичні значення критеріїв порівнюють з табличними при n-m-1 і m ступенях вільності і заданому рівні ймовірності p.

Якщо F_j>F_таб, то відповідна j-та пояснювальна змінна мультиколінеарна з іншими.

4. Знаходження частинних коефіцієнтів кореляції

(7.25)

5. Обчислення t-критеріїв

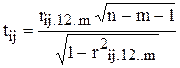(7.26)

Фактичні значення критеріїв t_ij порівнюють з табличними при n-m-1 ступенях вільності і рівні ймовірності p. Якщо , то між факторами x_i та x_j існує мультиколінеарність.

Усунення мультиколінеарності

Для усунення мультиколінеарності існує декілька способів:

1) якщо між двома факторами x_i та x_j існує мультиколінеарність, то один із факторів виключається з розгляду;

2) необхідно перетворити певним чином пояснювальні змінні:

а) і перевіряють на мультиколінеарність x_i і 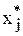. При відсутності її, розглядають фактор 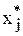замість x_j.

б) взяти відхилення від середньої;

в) замість абсолютних значень взяти відносні;

г) стандартизувати пояснювальні змінні.

За обчисленими F- та t-критеріями можна зробити такі висновки:

1. Якщо F-критерій більший за F_таб, тобто коли і-та змінна залежить від усіх інших, то необхідно вирішувати питання про її вилучення з переліку змінних.

2. Якщо |t_ij |> t_таб, то x_i та x_j тісно пов’язані між собою. Звідси, аналізуючи рівень обох видів критеріїв, можна зробити обґрунтований висновок про те, яку із змінних необхідно вилучити чи замінити іншою.

Заміна чи вилучення факторів завжди має узгоджуватися з економічною доцільністю, що випливає з мети дослідження.

У випадку, коли жоден з розглянутих способів не дає змоги позбутися мультиколінеарності, то параметри моделі слід оцінювати іншим методом, наприклад методом головних компонентів.

Дата добавления: 2014-01-07