Приклад. Використовуючи метод плинних середніх, провести згладжування за трирівневим інтервалом та експотенційне згладжування (α =0,2

Використовуючи метод плинних середніх, провести згладжування за трирівневим інтервалом та експотенційне згладжування (α =0,2, ).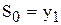

Періоди	Обсяг випуску тис.шт.	Згладжування ряду за трирівневим інтервалом	Експотенційне згладжування
		-	30,00
		30,67	30,20
		31,33	30,36
			30,69
		30,67	30,55
		30,67	30,44
			30,75
			30,80
		31,67	31,24
		31,67	31,19
		31,67	31,15
			31,52
		32,67	31,62
			31,90
		-	32,32

Аналітичне вирівнювання динамічного ряду здійснюється за допомогою кривих зростання.

Щоб правильно підібрати найкращу криву зростання для моделювання економічного явища необхідно знати особливості кожного виду кривих. Найчастіше використовується:

1. Поліноміальні прямі:

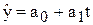· поліном першого степеня

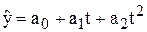· поліном другого степеня

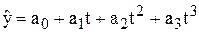· поліном третього степеня

....................................

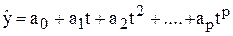· поліном степеня р

2. Гіперболічна функція

·

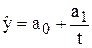
3. Експотенційна функція та її модифікації

·

·

·

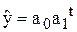
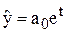
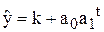
Параметри a₀, a₁, a₂ ….a_p мають конкретну інтерпретацію, що залежить від змісту процесу, який описується часовим рядом. Зокрема, а₁ характеризує швидкість зростання, а₂ – прискорення зростання, а₃ – зміну прискорення зростання.

Поліном другого порядку описує рух із рівномірною зміною прискорення як в додатному, так і в протилежному напрямку. Характерним для таких економічних процесів є рівноприскорене зростання або спад їх розвитку.

Експотенційна функція 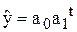описує процес із сталим темпом зростання і з сталим темпом приросту. Якщо 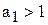, то крива зростає із збільшенням t, а при 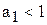- спадає.

Процеси, які характеризуються насиченням, описуються модифікованою експонентою .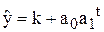

Вибір кривої, як правило, відбувається за згладженим рядом. Існує декілька підходів до вибору форми кривої:

1. Візуальний (графічний) тобто вибір форми тренду на основі графічного зображення динамічного ряду. На результат вибору впливає масштаб графічного зображення.

2. За критерій вибору форми тренду беруть суму квадратів відхилень значень рівнів від розрахункових, визначених на основі вирівняного ряду. Вибирають таку функцію, де така сума є найменшою.

3. Метод послідовних різниць,згідно із яким обчислюється перший, другий та вищі порядки різниць рівнів часового ряду:

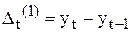
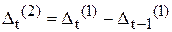
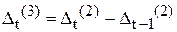
Обчислення проводяться доти, поки різниці не будуть майже однакові. Якщо різниці першого порядку майже рівні, то процес отримують прямою. Якщо різниці другого порядку - то поліном другого степеня, якщо різниці третього порядку майже рівні, то процес описується поліномом третього степеня і так далі.

Параметри кривих зростання можна визначити за допомогою МНК

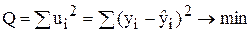
Згідно з цим методом необхідно розв’язати систему нормальних рівнянь, яка може мати різну кількість рівнянь в залежності від кількості параметрів кривої зростання.

Наприклад, для кривої 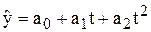отримаємо систему

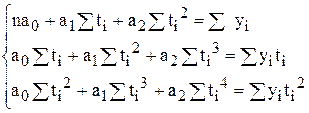
Для спрощення розрахунків можна використовувати метод умовного нуля. Якщо відлік значень t перенести в середину динамічного ряду, що розглядається, то 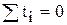. При непарній кількості членів ряду t приймає значення … -2, -1, 0, 1, 2 …, при парній – … -5, -3, -1, 1, 3, 5 ….

Приклад

Динаміка обсягів продажу товарів наведена в табл.

Показник	Роки
Річний обсяг продажу товарів, тис. шт.

Використовуючи лінійний тренд, спрогнозувати обсяги продажу товарів у 2010 році, припускаючи, що тенденції, які склались на даному ринку, сталі.

Для проведення прогнозу необхідно побудувати лінійне рівняння тренду, яке має вигляд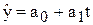

Виконаємо необхідні розрахунки:

Роки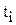
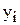
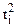
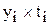
	-5			-75
	-3			-81
	-1			-41
S

Складемо систему рівнянь

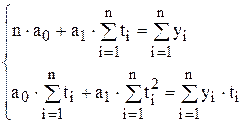
Отримаємо

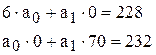
Звідси

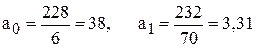
Отже, .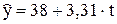

Використовуючи отримане рівняння тренду, розрахуємо прогнозне значення обсягів продажу на 2010 рік ():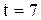

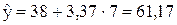(тис.шт.)

Отже, прогнозовані обсяги продажу товарів у 2010 році складають 61170 одиниць за умови збереження існуючих тенденцій, що склались на ринку.

Дата добавления: 2014-01-07