
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Складний рух точки
|
|
|
|
Лекція 4
3.1. Основні поняття
В класичній механіці прийняті умовно-нерухомі (інерціальні) системи відліку. Але в природі таких систем не існує, тому при розв'язуванні задач на практиці слід брати до уваги рухомість системи відліку.
Основною задачею кінематики складного руху точки є визначення основних його характеристик у двох різних системах координат (с. к.), якщо відомий взаємний відносний рух цих систем координат.
Введемо дві системи координат (див. рис. 3.1): умовно-нерухому с. к. - 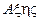 , і рухому с. к. -
, і рухому с. к. - 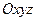 .
.
 Рис. 3.1.Системи координат при складному русі точки. Рис. 3.1.Системи координат при складному русі точки.
|
Розглянемо рух точки 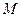 , приймаючи до уваги рухомість с. к. , приймаючи до уваги рухомість с. к. 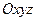 . Назвемо рух т. . Назвемо рух т. 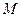 відносно рухомої с. к. ( відносно рухомої с. к. ( ) відносним, відносно нерухомої с. к. ( ) відносним, відносно нерухомої с. к. ( ) - абсолютним, і введемо поняття переносного руху (див. також рис. 3.2).
Переносним рухом будемо називати рух тієї точки рухомого середовища, з якою у даний момент часу збігається рухома точка, відносно нерухомої системи координат. ) - абсолютним, і введемо поняття переносного руху (див. також рис. 3.2).
Переносним рухом будемо називати рух тієї точки рухомого середовища, з якою у даний момент часу збігається рухома точка, відносно нерухомої системи координат.
|
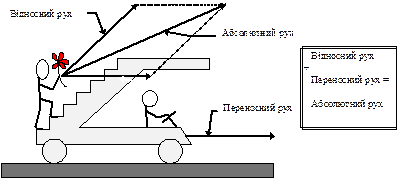
Рис. 3.2. До визначення відносного, переносного і абсолютного рухів.
Визначимо положення т. 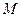 у цих двох системах координат векторним способом.
у цих двох системах координат векторним способом.
Проведемо радіус-вектор 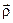 із т.
із т. 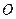 в т.
в т. 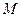 . Тоді співвідношення
. Тоді співвідношення
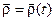
| (3.1) |
будемо називати кінематичним рівнянням відносного руху точки.
Положення т. 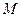 у нерухомій с. к. визначається радіус-вектором
у нерухомій с. к. визначається радіус-вектором 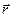 , а положення початку
, а положення початку 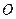 рухомої с. к. відносно нерухомої - радіус-вектором
рухомої с. к. відносно нерухомої - радіус-вектором 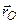 .
.
3.2. Формула Бура
Розглянемо вираз вектора 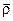 через його проекції в рухомій системі координат
через його проекції в рухомій системі координат
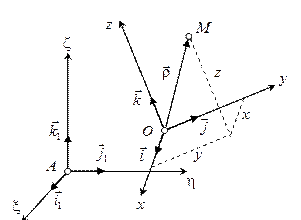
| з ортами 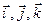 (рис. 3.3): (рис. 3.3):
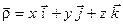 ,
і знайдемо абсолютну похідну від нього ,
і знайдемо абсолютну похідну від нього
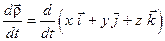 .
Оскільки система координат .
Оскільки система координат 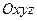 рухається довільним чином відносно рухається довільним чином відносно 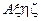 , тому її одиничні вектори (орти) , тому її одиничні вектори (орти) 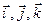 не є сталими, і вираз абсолютної похідної набуде вигляду не є сталими, і вираз абсолютної похідної набуде вигляду
|
Рис. 3.3. До визначення вектора 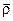 . .
|
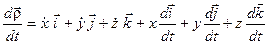 . .
| (3.2) |
У формулі (3.2) перші три доданки характеризують зміну вектора 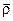 в рухомій системі координат, тобто їх сума є відносною похідною
в рухомій системі координат, тобто їх сума є відносною похідною
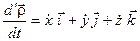 . .
| (3.3) |
Останні три доданки у формулі (3.2) позначимо 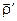 , тобто
, тобто
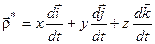 . .
| (3.4) |
Помножимо скалярно обидві частини виразу (3.4) послідовно на орти 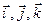
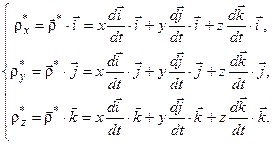
| (3.5) |
Отримаємо деякі допоміжні співвідношення
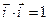
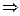
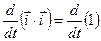
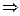
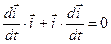
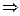
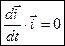 ;
;
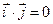
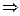
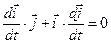
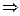
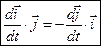 .
.
Введемо наступні позначення:
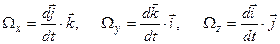 , ,
| (3.6) |
тоді формули (3.5) набудуть вигляду
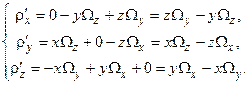
| (3.7) |
Ці вирази повністю збігаються з виразами проекцій векторного добутку 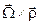 на осі системи координат
на осі системи координат 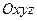 . Дійсно
. Дійсно
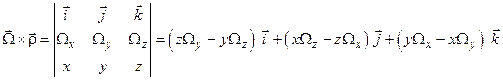 .
.
Тому має місце вираз
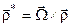 , ,
| (3.8) |
з урахуванням якого формула (3.2) набуває остаточного вигляду
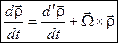
| (3.9) |
і називається формулою Бура.
Таким чином, абсолютна похідна від векторної функції 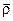 за скалярним аргументом
за скалярним аргументом 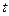 дорівнює сумі відносної похідної тієї ж функції та векторного добутку вектора
дорівнює сумі відносної похідної тієї ж функції та векторного добутку вектора 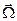 на
на 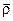 .
.
Формула Бура може застосовуватись до будь-якої неперервної векторної функції довільного скалярного аргументу і широко застосовується в розділі кінематики.
Наведемо деякі частинні випадки формули Бура.
1) Припустимо, що система координат 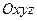 є нерухомою відносно
є нерухомою відносно 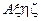 , або рухається поступально.
, або рухається поступально.
В цьому випадку, оскільки орти 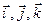 є сталими, за формулами (3.6) маємо
є сталими, за формулами (3.6) маємо 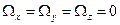 ,
, 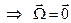 , і тоді формула Бура набуває вигляду
, і тоді формула Бура набуває вигляду 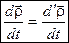 .
.
2) Припустимо, що вектор 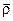 не змінюється в рухомій системі координат
не змінюється в рухомій системі координат 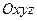 , тоді
, тоді 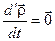 і отримуємо
і отримуємо 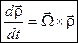 .
.
3) Припустимо, що вектор 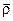 не змінюється в нерухомій системі координат
не змінюється в нерухомій системі координат  , тобто
, тобто 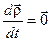 . Тоді маємо
. Тоді маємо 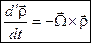 .
.
Визначимо швидкість і прискорення точки відносно нерухомої с. к. за допомогою формули Бура, для чого доведемо дві теореми.
3.3. Теорема про додавання швидкостей
На підставі рисунку 3.1 можна записати наступне співвідношення, що зв'язує радіус-вектори 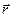 ,
, 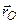 і
і 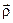 :
:
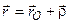 . .
| (3.10) |
Визначимо тепер абсолютну швидкість т. 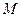 , пам’ятаючи при диференціюванні рівності (3.10), що радіус-вектори і орти є функціями часу, -
, пам’ятаючи при диференціюванні рівності (3.10), що радіус-вектори і орти є функціями часу, -
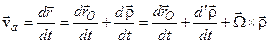 , ,
| (3.11) |
а оскільки т. 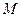 має у рухомій с. к. координати
має у рухомій с. к. координати 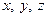 (тобто
(тобто 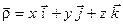 ), то можна записати співвідношення (3.11) у наступному вигляді:
), то можна записати співвідношення (3.11) у наступному вигляді:
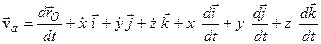 . .
| (3.12) |
Зупинимо переносний рух, тобто зафіксуємо положення рухомої с. к. відносно нерухомої. В цьому випадку вектори 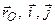 і
і 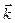 будуть постійними і тоді вираз
будуть постійними і тоді вираз
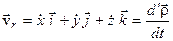
| (3.13) |
представляє відносну швидкість т. 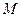 , - фізичну величину, яка характеризує швидкість зміни положення точки у її відносному русі.
, - фізичну величину, яка характеризує швидкість зміни положення точки у її відносному русі.
Потім «зупинимо» відносний рух, тобто будемо вважати, що положення т. 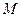 у рухомій с. к. не змінюється (тобто координати
у рухомій с. к. не змінюється (тобто координати 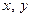 і
і 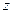 є сталими величинами). Тоді з формули (3.12) отримаємо вираз
є сталими величинами). Тоді з формули (3.12) отримаємо вираз
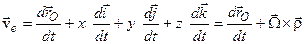 , ,
| (3.14) |
який характеризує швидкість зміни положення т. 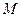 у переносному русі і називається переносною швидкістю.
у переносному русі і називається переносною швидкістю.
Враховуючи введені означення, формулу (3.12) можна переписати наступним чином:
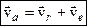 . .
| (3.15) |
Таким чином доведена теорема про додавання швидкостей: абсолютна швидкість точки (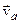 ) при складному її русі дорівнює векторній сумі відносної (
) при складному її русі дорівнює векторній сумі відносної (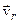 ) та переносної (
) та переносної (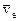 ) швидкостей.
) швидкостей.
3.4.Теорема про додавання прискорень (теорема Коріоліса)
Знайдемо абсолютне прискорення т. 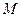 . Для цього продиференціюємо вираз (3.12) для абсолютної швидкості цієї точки за часом:
. Для цього продиференціюємо вираз (3.12) для абсолютної швидкості цієї точки за часом:
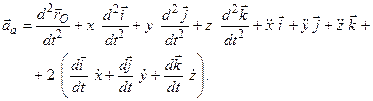
| (3.16) |
Знову «зупинимо» переносний рух, зафіксувавши положення рухомої с. к. відносно нерухомої. Тоді вектори 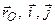 і
і 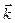 є сталими і із рівності (3.16), враховуючи, що в цьому випадку абсолютне прискорення
є сталими і із рівності (3.16), враховуючи, що в цьому випадку абсолютне прискорення 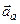 збігається з відносним
збігається з відносним 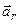 , маємо
, маємо
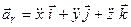 . .
| (3.17) |
Якщо тепер уявно зупинити т. 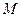 , то тоді абсолютне прискорення
, то тоді абсолютне прискорення 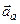 стає рівним переносному прискоренню
стає рівним переносному прискоренню 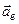 , і, помітивши, що відносні координати т.
, і, помітивши, що відносні координати т. 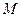 -
- 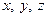 залишаються сталими, із рівності (3.16) отримаємо
залишаються сталими, із рівності (3.16) отримаємо
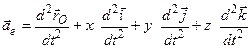 . .
| (3.18) |
Таким чином, у формулі (3.16) залишився непозначеним доданок
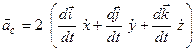 , ,
| (3.19) |
що називається прискоренням Коріоліса (поворотним прискоренням). Ця фізична величина характеризує швидкість зміни переносної швидкості у відносному русі і відносної швидкості у переносному (фізичний зміст прискорення Коріоліса).
Зробимо більш детальний аналіз цього прискорення.
Перш за все відмітимо, що у випадку переносного поступального руху прискорення Коріоліса відсутнє (у цьому разі орти 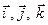 є векторними константами і похідні від них за часом обертаються в нуль). Наприклад,
є векторними константами і похідні від них за часом обертаються в нуль). Наприклад, 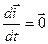 .
.
У випадку переносного обертального руху навколо будь-якої осі  (див. рис. 3.4) маємо наступні співвідношення (за формулою Ейлера)
(див. рис. 3.4) маємо наступні співвідношення (за формулою Ейлера)
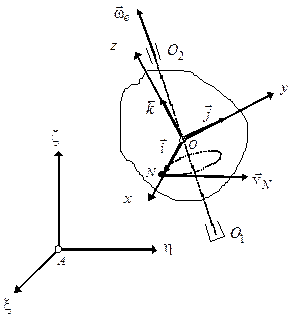 Рис. 3.4.До виводу формули Коріоліса.
Рис. 3.4.До виводу формули Коріоліса.
| 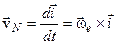 , а крім того, за аналогією, , а крім того, за аналогією,
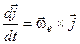 , ,
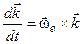 . (3.20)
Тоді, подставивши ці співвідношення (3.20) у формулу (3.19), отримаємо вираз . (3.20)
Тоді, подставивши ці співвідношення (3.20) у формулу (3.19), отримаємо вираз
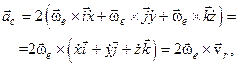 або
або
|
яке представляє формулу Коріоліса, що читається наступним чином:
| прискорення Коріоліса дорівнює подвоєному векторному добутку вектора кутової швидкості переносного руху і вектора відносної (лінійної) швидкості точки. |
Підставивши тепер вирази (3.17) - (3.19) в (3.16), будемо мати
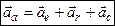 , ,
| (3.22) |
що є математичним записом теореми Коріоліса:
| абсолютне прискорення точки дорівнює векторній сумі трьох прискорень: переносного, відносного і коріолісового. |
За формулою (3.21) знайдемо модуль коріолісового прискорення
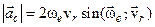 . .
| (3.23) |
Коріолісове прискорення дорівнює нулю у трьох випадках:
1) 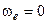 (переносний рух - поступальний);
(переносний рух - поступальний);
2) 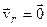 - точка у відносному русі зупинилася.
- точка у відносному русі зупинилася.
3) 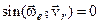 , тобто вектори
, тобто вектори 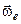 і
і 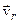 колінеарні (що звичайно позначається так:
колінеарні (що звичайно позначається так: 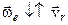 ).
).
Завдання: шляхом диференціювання формули (3.11) та подальшого аналізу довести, що 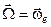 .
.
Задача: Компресор з криволінійними каналами обертається навколо осі 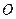 із заданою кутовою швидкістю
із заданою кутовою швидкістю 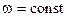 . Повітря тече по каналам з постійною відносною швидкістю
. Повітря тече по каналам з постійною відносною швидкістю 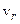 . Знайти проекції абсолютної швидкості та прискорення на осі координат для частки повітря, що знаходиться у точці
. Знайти проекції абсолютної швидкості та прискорення на осі координат для частки повітря, що знаходиться у точці 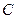 каналу
каналу 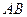 , якщо радіус кривини каналу у точці
, якщо радіус кривини каналу у точці 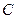 дорівнює
дорівнює 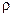 , а кут між нормаллю до кривої
, а кут між нормаллю до кривої 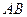 у точці
у точці 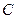 і радіусом
і радіусом 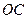 дорівнює
дорівнює 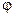 . Радіус
. Радіус 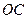 дорівнює
дорівнює 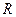 (див. рис. 3.4).
(див. рис. 3.4).
Дано: 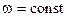 ,
, 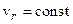 ,
, 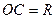 ,
, 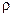 ,
, 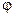 .
.
Знайти: 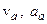 .
.
 Рис. 3.4.Компресор з криволінійними каналами.
Рис. 3.4.Компресор з криволінійними каналами.
| Розв'язання
Рух по каналу 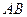 є відносним рухом, а крива є відносним рухом, а крива 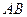 являє собою траєкторію відносного руху. Рух т. являє собою траєкторію відносного руху. Рух т. 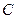 відносно нерухомої системи координат - абсолютний, його траєкторія - спіраль. Переносний рух – це рух тієї точки каналу, в якій у даний момент часу знаходиться т. відносно нерухомої системи координат - абсолютний, його траєкторія - спіраль. Переносний рух – це рух тієї точки каналу, в якій у даний момент часу знаходиться т. 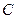 , тобто по колу радіуса , тобто по колу радіуса 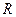 .
Для знаходження .
Для знаходження 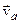 скористаємося теоремою про додавання швидкостей скористаємося теоремою про додавання швидкостей
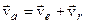 .
Обчислюємо .
Обчислюємо 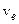 із рівняння обертального руху, «зупинивши» відносний рух: із рівняння обертального руху, «зупинивши» відносний рух:
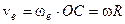 . .
|
Тоді
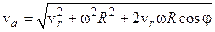 .
.
Для визначення абсолютного прискорення застосуємо теорему про додавання прискорень
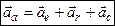 .
.
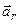 визначимо, «зупинивши» переносний рух колеса і згадавши отримані раніше співвідношення для складових повного прискорення при довільному криволінійному русі (див. рис. 3.5 а) і при обертанні точки навколо нерухомої осі (рис. 3.5 b):
визначимо, «зупинивши» переносний рух колеса і згадавши отримані раніше співвідношення для складових повного прискорення при довільному криволінійному русі (див. рис. 3.5 а) і при обертанні точки навколо нерухомої осі (рис. 3.5 b):
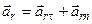 ,
,
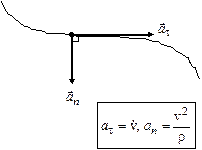
| 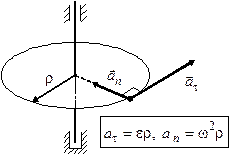
|
| (a) Довільний криволінійний рух | (b) Обертання навколо нерухомої осі |
| Рис. 3.5.Співвідношення для складових повного прискорення. |
де 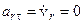 (оскільки
(оскільки 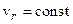 ),
), 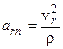 , звідки випливає, що
, звідки випливає, що 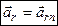 .
.
Для визначення 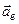 «зупинимо» відносний рух, тоді маємо
«зупинимо» відносний рух, тоді маємо
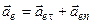 ,
,
причому
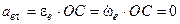 (оскільки
(оскільки 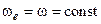 ),
),
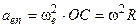 .
.
Таким чином, 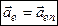 .
.
Коріолісове прискорення знайдемо, скориставшись формулою:
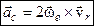 ,
,
а саме:
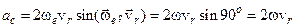 .
.
Потім знаходиться абсолютне прискорення 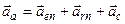 шляхом проектування кожного з векторів правої частини на осі
шляхом проектування кожного з векторів правої частини на осі  ; знаходження сум проекцій вказаних векторів на осі
; знаходження сум проекцій вказаних векторів на осі 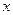 і
і 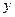 -
- 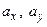 , і визначення модуля вектора абсолютного прискорення
, і визначення модуля вектора абсолютного прискорення 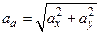 .
.
Отже, маємо:
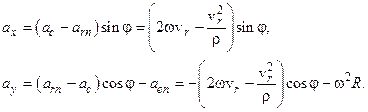
Тоді остаточно отримаємо:
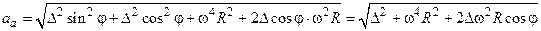 ,
,
де 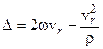 .
.
Відповідь: 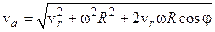 ,
, 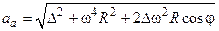 ,
,
де 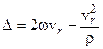 .
.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1351; Нарушение авторских прав?; Мы поможем в написании вашей работы!