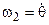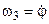КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Кути Ейлера
|
|
|
|
Нехай тіло 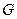 , з яким жорстко зв’язана с. к.
, з яким жорстко зв’язана с. к. 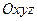 , здійснює (сферичний) рух у нерухомій с. к.
, здійснює (сферичний) рух у нерухомій с. к.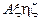 , причому початки обох систем збігаються із нерухомою точкою
, причому початки обох систем збігаються із нерухомою точкою 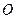 .
.

| Положення т. 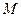 в нерухомій системі координат визначає радіус-вектор в нерухомій системі координат визначає радіус-вектор 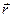 , а в рухомій ( , а в рухомій (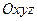 ) – вектор ) – вектор 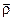 (див. рис. 6.2) (див. рис. 6.2)
Перетворення координат точки від рухомої системи координат до нерухомої може бути подано таким чином:
або у матричній формі -
| ||||||
| Рис. 6.2.Системи координат при сферичному русі твердого тіла. |
Рівняння (6.2) або (6.3) є кінематичними рівняннями руху тіла з однією нерухомою точкою.
В них коефіцієнти 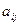 є функціями трьох незалежних величин – кутів Ейлера: прецесії (
є функціями трьох незалежних величин – кутів Ейлера: прецесії (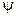 ), нутації (
), нутації (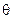 ), та власного обертання (
), та власного обертання ( ).
).
За допомогою рівнянь (6.2) або (6.3) можна визначити положення точки тіла в нерухомій системі координат 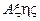 .
.
Теорема 1 (Ейлера): довільне переміщення твердого тіла з нерухомою точкою можна здійснити за допомогою трьох послідовних поворотів навколо вибраних визначеним чином осей.
Нехай у початковий момент часу осі нерухомої і рухомої с. к. із загальним початком у нерухомій точці 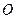 збігаються (
збігаються ( з
з 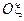 ,
, 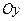 з
з 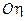 ,
, 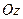 з
з 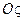 ).
).
Здійснимо три послідовних повороти тіла, осі, кути і відповідні кутові швидкості яких вказані у табл. 6.1 і показані на рис. 6.3.
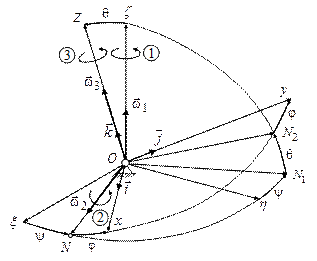
| Таблиця 6.1. Кути Ейлера
Оскільки кожному моменту часу відповідає означене положення тіла і означені кути Ейлера, тому залежності
| ||||||||||||||||
| Рис. 6.3. Повороти і кути Ейлера. |
можуть бути прийняті в якості кінематичних рівнянь руху тіла, що обертається навколо нерухомої точки. Одночасно вони визначають закон руху твердого тіла з нерухомою точкою.
Знайдемо миттєву кутову швидкість 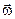 обертання твердого тіла з нерухомою точкою (див. п. 4.2):
обертання твердого тіла з нерухомою точкою (див. п. 4.2):
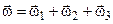 . .
| (6.4) |
Оскільки з рис. 6.3 випливає, що 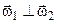 і
і 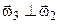 , то складаючи спочатку за правилом паралелограма
, то складаючи спочатку за правилом паралелограма 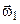 і
і 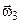 (кут між ними
(кут між ними 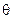 ), отримаємо:
), отримаємо: 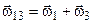 , а використавши теорему косинусів, знайдемо модуль цього вектора
, а використавши теорему косинусів, знайдемо модуль цього вектора
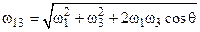 .
.
Врахувавши потім, що 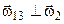 , знайдемо шукану миттєву кутову швидкість
, знайдемо шукану миттєву кутову швидкість
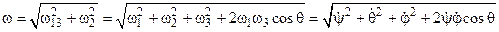 .
.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1668; Нарушение авторских прав?; Мы поможем в написании вашей работы!
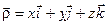 .
.
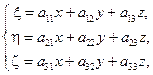
 .
.
 [1]
[1]