
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основні правила диференціювання
|
|
|
|
1. (u 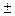 v) ' = u'
v) ' = u'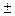 v'
v'
2. (c u) ' = c(u)'
3. (u v)' = u'v + uv'
4. 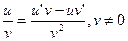
5. Похідна складної функції: (f (g (x))) ' = f '(g (x)) g'(x)
g'(x)
Доведення деяких формул з таблиці похідних.
 1. c'=
1. c'=
 .
.
3. (sin x)'=
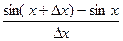 =
= .
.
Доведення деяких правил диференціювання.
1) (u+v) '=lim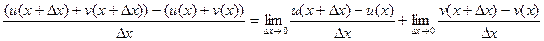 .
.
5) (f(g(x)))'=
= .
.
Вправа. Подумати над доведенням інших формул.
Роздивившись таблицю похідних основних елементарних функцій та таблицю правил диференціювання отримуємо теорему.
Теорема. Похідна елементарної функції є також елементарною функцією.
Приклади. 1)

 .
.
2)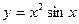
 .
.
3)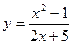
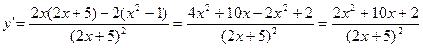 .
.
4)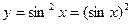
 .
.
5)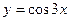
 .
.
6)
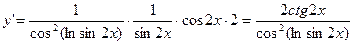 .
.
7)
 .
.
Знаходження похідної з допомогою логарифмування
(логарифмічне диференціювання)
Логарифмічне диференціювання полягає в тому, що перш ніж взяти похідну, функцію логарифмують за основою е: у=f(x), ln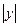 = ln
= ln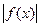 , тоді, після спрощення правої частини за властивостями логарифмів, беруть похідну з лівої і правої частини та з отриманого рівняння виражають похідну у'.
, тоді, після спрощення правої частини за властивостями логарифмів, беруть похідну з лівої і правої частини та з отриманого рівняння виражають похідну у'.
Цей метод використовують коли функція є складним добутком, часткою чи степенем, бо при логарифмуванні вони спрощуються.
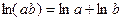
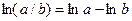
 .
.
Приклад. y = (sin x)x.
Функція визначена в околі точки х, якщо sin x>0. Тільки в таких точках можна шукати похідну.
ln у=ln(sin x)x=x ln(sin x)
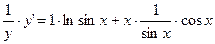
y' = y (ln sin x + x ctg x)= (sin x)x (ln sin x + x ctg x).
Вправа. Знайти похідну функції  .
.
Диференціал функції
Приклад. Знайдемо приріст функції 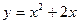 в точці в т.х0=3 при довільному малому приросту аргументу
в точці в т.х0=3 при довільному малому приросту аргументу 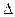 х.
х. 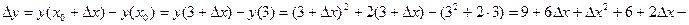
 . Отже приріст функції розбився на дві частини: перша – головна частина приросту має вигляд с
. Отже приріст функції розбився на дві частини: перша – головна частина приросту має вигляд с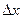 , де с – число, друга є функцією від
, де с – число, друга є функцією від 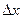 – набагато меншою від
– набагато меншою від 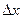 при малих
при малих 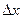 , кажуть нескінченно малою вищого порядку ніж
, кажуть нескінченно малою вищого порядку ніж 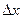 при
при  . Якщо знайти границю
. Якщо знайти границю  .
.
Функція y=f(x) називається диференційованою в т.х0, якщо її приріст в цій точці можна подати у вигляді: 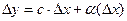 , де с – число, а
, де с – число, а  – функція від
– функція від 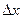 – нескінченно мала вищого порядку ніж
– нескінченно мала вищого порядку ніж 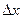 при
при  , тобто
, тобто 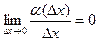 .
.
Тоді основну частину приросту функції, а саме  називають диференціалом функції в т. х0 . Позначення:
називають диференціалом функції в т. х0 . Позначення: 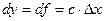 .
.
Теорема (про зв’язок похідної і диференціалу). Функція диференційована в точці тоді і тільки тоді, коли існує похідна в цій точці. Тоді  а тому
а тому
 .
.
Доведення. Нехай f диференційована в т. х0 . Знайдемо похідну функції 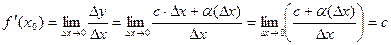 , тобто існує похідна рівна с.
, тобто існує похідна рівна с.
Нехай існує  . Доведемо, що f диференційована в точці х0. Позначимо вираз
. Доведемо, що f диференційована в точці х0. Позначимо вираз 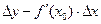 через
через  і доведемо, що він є нескінченно малим вищого порядку ніж
і доведемо, що він є нескінченно малим вищого порядку ніж 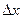 при
при  .
.
 . Теорема доведена.
. Теорема доведена.
Операції знаходження похідної або диференціалу називають диференціюванням функції. Функція називається диференційованою на інтервалі, якщо вона диференційована в кожній точці інтервалу.
Теорема (про зв’язок диференціювання і неперервності). Диференційована в точці функція є неперервною в ній.
Доведення. Нехай функція диф. в точці. Тоді 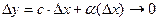 , при
, при  .
.
Навпаки не завжди правильно.
Приклад. 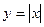 – неперервна на
– неперервна на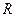 , але не існує похідної в точці 0, бо
, але не існує похідної в точці 0, бо 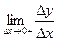 = =
= =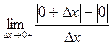 =
=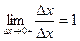 . Аналогічно для лівої границі отримаємо -1. Отже, дана границя не існує.(Можна також побачити на графіку
. Аналогічно для лівої границі отримаємо -1. Отже, дана границя не існує.(Можна також побачити на графіку 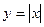 в точці 0 є кут, тому нема дотичної).
в точці 0 є кут, тому нема дотичної).
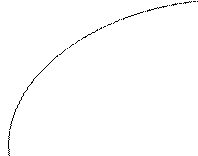
Геометричний і практичний зміст диференціалу
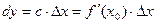 . Але
. Але  , де k – кутовий коефіцієнт дотичної в т. х0.
, де k – кутовий коефіцієнт дотичної в т. х0.
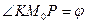


 f(х0+
f(х0+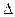 х) K
х) K

 у=f(х)
у=f(х)
 |
 dy
dy
М0  y
y

 f(х0)
f(х0) 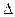 x P
x P
 х0 х0+
х0 х0+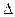 х
х
З 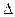 M0PK: dy= tg
M0PK: dy= tg
 – приріст дотичної. Отже, геометричний зміст диференціалу: диференціал функції в точці це приріст дотичної в даній точці.
– приріст дотичної. Отже, геометричний зміст диференціалу: диференціал функції в точці це приріст дотичної в даній точці.
Якщо 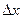 - мале, то приріст дотичної мало відрізняється від приросту самої функції
- мале, то приріст дотичної мало відрізняється від приросту самої функції 
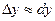 . Це ж випливає і з означення диференційованості в точці, бо величиною
. Це ж випливає і з означення диференційованості в точці, бо величиною  , яка є набагато меншою від
, яка є набагато меншою від 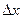 можна знехтувати. Отже, практичний зміст диференціалу:
можна знехтувати. Отже, практичний зміст диференціалу: 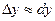 при малих
при малих 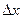 .
.
Дану формулу часто використовують в наближених обчисленнях.
Приклад. Обчислити наближено arctg 1,01.
Розглянемо функцію у=arctg x. Відомо, що arctg 1=  . Приріст аргументу
. Приріст аргументу
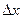 =1,01-1=0,01 – досить малий. Можна замінити
=1,01-1=0,01 – досить малий. Можна замінити 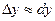 . Обчислимо
. Обчислимо 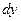 в точці х=1.
в точці х=1.  Тоді
Тоді
arctg 1,01=arctg 1+ arctg 1+
arctg 1+ 3,1416/4+0,005=0,7854+0,005
3,1416/4+0,005=0,7854+0,005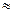 0,79.
0,79.
Нова формула для диференціалу


Приклади. 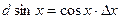


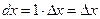 .
.
Отже, формулу для диференціалу можна переписати у вигляді: 
Приклади. 1)  2)
2)  .
.
Нова формула для диференціалу має дуже зручну властивість.
Теорема (про інваріантність форми диференціалу). Формула  є правильною також коли х є внутрішньою функцією х=х(t).
є правильною також коли х є внутрішньою функцією х=х(t).
Доведення. Нехай х=х(t).  .
.
Отже, диференціал можна брати від функції поступово.
Приклад. 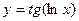
 .
.
Також можна проводити обернену операцію – підведення під знак диференціалу: 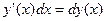 (також можна поступово (див. нижче пр.3)).
(також можна поступово (див. нижче пр.3)).
Приклади. 1)  2)
2) 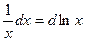 3)
3) 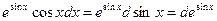 .
.
Із формули  виразимо
виразимо 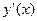 :
: 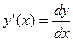 – тобто, похідна дорівнює відношен-ню диференціалів. Це формула для обчислення похідної через диференціали. Вона правильна і тоді коли х незалежна змінна і коли х є внутрішньою функцією. Щоб підкреслити те, що похідна з функції у береться саме по змінній х використовують таке позначення
– тобто, похідна дорівнює відношен-ню диференціалів. Це формула для обчислення похідної через диференціали. Вона правильна і тоді коли х незалежна змінна і коли х є внутрішньою функцією. Щоб підкреслити те, що похідна з функції у береться саме по змінній х використовують таке позначення  . Також як позначення похідної з функції у по змінній х часто використовують вираз
. Також як позначення похідної з функції у по змінній х часто використовують вираз  .
.
Правила диференціювання.
(Випливають із відповідних правил знаходження похідної і формули  .)
.)
dc=0 d(uv)=vdu+udv
d(cu)=c du 
d(u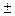 v)=du
v)=du 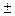 dv
dv
Похідна параметрично заданої функції
Кажуть функція у від х задана параметрично, якщо 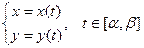 . Тут t – параметр.
. Тут t – параметр.
Інколи можна з першого рівняння виразити t через х і, підставивши його в друге рівняння, отримати залежність у від х в звичайному, кажуть в явному вигляді.
Приклад. 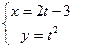 – параметрично задана функція.
– параметрично задана функція.
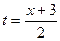 ,
, 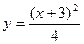 – та ж функція але задана явно.
– та ж функція але задана явно.
Можна зразу ж шукати похідну  з параметрично заданої функції, використавши формулу для похідної через диференціали.
з параметрично заданої функції, використавши формулу для похідної через диференціали.
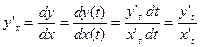 . Функція
. Функція  тут залежить від параметру t як і функція у=у(t). Щоб розглядати її як функцію від змінної х, дописують ще залежність х від t:
тут залежить від параметру t як і функція у=у(t). Щоб розглядати її як функцію від змінної х, дописують ще залежність х від t: 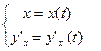 . Отже, похідна параметрично заданої функції вийшла також параметрично задана функція.
. Отже, похідна параметрично заданої функції вийшла також параметрично задана функція.
Приклад. 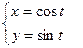
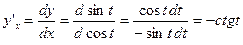

Похідна оберненої функції.
Нехай функція у=у(х) має обернену х=х(у).
Оскільки , то аналогічно
, то аналогічно  .
.
Приклад. у=arcsin x – обернена функція до х= sin y, y є [- ].
].  , то
, то 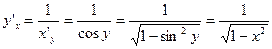 . (Враховано, що
. (Враховано, що 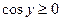 на даному проміжку.)
на даному проміжку.)
Похідна неявно заданої функції
F(x,y)=0 – це рівняння задає залежність у від х неявно. Кажуть неявно задана функція. Тут F - функція двох змінних.
Інколи з нього можна виразити у через х і отримати явну залежність у=у(х). Може вийти кілька функцій.
Приклад. 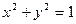 – неявно задана функція.
– неявно задана функція.  – отримали дві явно задані функції.
– отримали дві явно задані функції.
Можна шукати похідну зразу для неявно заданої функції. Для цього беруть диференціали з обох сторін рівняння, що задає функцію. Тут стають в пригоді правила для диференціалів. Потім з отриманої рівності виражають потрібну похідну 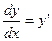 .
.
Приклад. 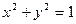 . Візьмемо диференціали з обох сторін рівняння:
. Візьмемо диференціали з обох сторін рівняння:

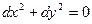


 .
.
Зауваження. Похідна виражається не тільки через х, але й через значення у в точці х.
Отже, якщо потрібно знайти похідну в точці х0, то прийдеться також знайти у(х0) з початкового рівняння.
Продовження прикладу. 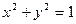 . Знайти
. Знайти 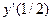 .
.  . Щоб знайти у(1/2) підставимо х=1/2 в початкове рівняння:
. Щоб знайти у(1/2) підставимо х=1/2 в початкове рівняння:  ,
,  . Тоді
. Тоді  . Отже, рівняння
. Отже, рівняння 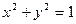 задає дві функції, для однієї з них похідна в точці ½ дорівнює
задає дві функції, для однієї з них похідна в точці ½ дорівнює 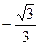 , а для іншої дорівнює
, а для іншої дорівнює  .
.
Похідні вищих порядків
Нехай для функції у=f(х) існує похідна в кожній точці деякого проміжку Х. Тоді 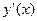 є також функцією на Х. Для неї знову можна шукати похідну по змінній х. Вона називається похідною другого порядку для початкової функції. Позначається
є також функцією на Х. Для неї знову можна шукати похідну по змінній х. Вона називається похідною другого порядку для початкової функції. Позначається 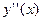 або
або 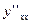 ,
,  .
. 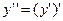 .
.
Аналогічно 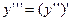 -- похідна третього порядку і т. д.
-- похідна третього порядку і т. д.
Позначення: 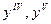 -- четверта, п’ята похідні (римськими цифрами), або
-- четверта, п’ята похідні (римськими цифрами), або 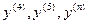 – четверта, п’ята, n-та похідні (арабськими цифрами в дужках).
– четверта, п’ята, n-та похідні (арабськими цифрами в дужках).
Також зустрічаються позначення через диференціали: 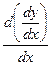 =
= а—формула для знаходження похідної ІІ-го порядку через диференціали і позначення.
а—формула для знаходження похідної ІІ-го порядку через диференціали і позначення.
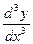 ,
, 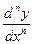 – третя, n-та похідні функції у по змінній х.
– третя, n-та похідні функції у по змінній х.
Приклад. 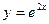 ,
, 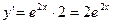 ,
, 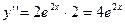 ,
, 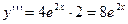 ,…,
,…, 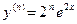 .
.
Похідні вищих порядків параметрично заданої функції
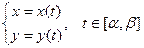 ,
, 
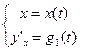 – знову параметрично задана функція. Аналогічно знаходимо для неї похідну по змінній х. Позначаємо
– знову параметрично задана функція. Аналогічно знаходимо для неї похідну по змінній х. Позначаємо  або
або 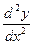 .
. 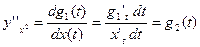 – функція від t. Добавляємо залежність х(t):
– функція від t. Добавляємо залежність х(t):  – параметрично задана функція. Можна ще шукати похідну, яка буде вже похідною третього порядку для початкової функції.
– параметрично задана функція. Можна ще шукати похідну, яка буде вже похідною третього порядку для початкової функції.
Приклад. 
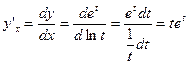
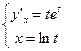
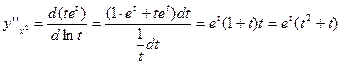
 . Можна шукати
. Можна шукати  і т.д.
і т.д.
Основні теореми про диференційовані функції
Теорема Лагранжа (про скінченні прирости). Якщо функція f неперервна на відрізку [a,b] і диференційована на (а,b), тоді існує точка с є (a,b) така, що f(b)-f(a)= f '(c)(b-a).
Ліва частина рівності це приріст функції на [a,b], в правій частині є (b-a) – приріст аргументу. Отже, формула точно виражає приріст функції через приріст аргументу:  .
.
 Геометричний зміст: Якщо поділити на (b-a):
Геометричний зміст: Якщо поділити на (b-a): 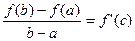 . Зліва у формулі стоїть tg
. Зліва у формулі стоїть tg =k – кутовий коефіцієнт січної MN. Справа – кутовий коефіцієнт дотичної в точці с. їх рівність означає паралельність січної і дотичної. Отже, теорема стверджує, що якщо крива гладка, то існує
=k – кутовий коефіцієнт січної MN. Справа – кутовий коефіцієнт дотичної в точці с. їх рівність означає паралельність січної і дотичної. Отже, теорема стверджує, що якщо крива гладка, то існує
т. с є (a,b) така, що дотична в точці c є паралельною до січної, що проходить через точки з абсцисами a, b.
Теорема (правило Лопіталя – розкриття невизначеностей 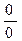 і
і  ). Нехай частка функцій
). Нехай частка функцій  визначена в деякому проколотому околі точки а і потрібно знайти границю
визначена в деякому проколотому околі точки а і потрібно знайти границю  , але за теоремою про арифметичні дії над границями виходить невизначеність
, але за теоремою про арифметичні дії над границями виходить невизначеність 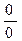 або
або  . Тоді, якщо існує границя частки похідних
. Тоді, якщо існує границя частки похідних  =L (L – число чи нескінченність), то також існує початкова границя рівна L:
=L (L – число чи нескінченність), то також існує початкова границя рівна L:  .
.
Коротко: 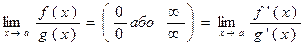 , якщо остання границя існує.
, якщо остання границя існує.
Зауваження 1. Якщо границя частки похідних не існує, то про початкову границю не можна зробити ніякого висновку. Вправа.  .
.
2. Правило Лопіталя можна застосовувати і для односторонніх границь і при а =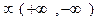 .
.
3. Правило Лопіталя можна застосовувати кілька разів підряд, поки виходять вказані невизначеності.
Доведення. (для неперервних разом з своїми похідними в деякому околі точки а функцій)
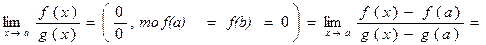
= .
.
Приклади. 1. 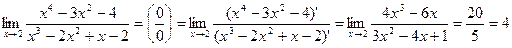 . Оскільки остання границя число, то рівність правильна.
. Оскільки остання границя число, то рівність правильна.
2.  .
.
3.  .
.
Зауваження. Інші види невизначеностей можна тотожними перетвореннями виразів звести до невизначеностей 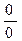 або
або  .
.
Приклади. 1.  =…
=…
Вправа. Доробити границю за правилом Лопіталя.
2. 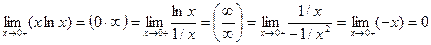 .
.
Для степеневих невизначеностей: 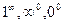 користуються формулою
користуються формулою 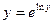 і неперервністю функції
і неперервністю функції  .
.
3. 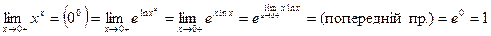 .
.
Теорема (формула) Тейлора
Якщо функція диференційована в точці в т. х0, то можна записати
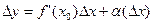 , де
, де  – нескінченно мала вищого порядку ніж
– нескінченно мала вищого порядку ніж 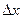 при
при  , тобто при
, тобто при  .
.
Розпишемо прирости: 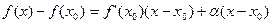 , те саме:
, те саме: 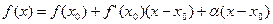 – це є формула Тейлора при n=1.
– це є формула Тейлора при n=1.
Теорема. Якщо для функції f(x) існують похідні до n-того порядку в деякому околі точки х0, то справедлива формула Тейлора:  де
де  – нескінченно мала вищого порядку ніж
– нескінченно мала вищого порядку ніж  при
при  , цей вираз називається ще залишковим членом формули Тейлора. Залишковий член можна виписати точніше (у формі Лагранжа):
, цей вираз називається ще залишковим членом формули Тейлора. Залишковий член можна виписати точніше (у формі Лагранжа):  , де точка с належить інтервалу з кінцями х0 та х.
, де точка с належить інтервалу з кінцями х0 та х.
Зауваження. Формула Лагранжа у вигляді 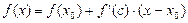 , де с є (х0,х) є формулою Тейлора при n =0 із залишковим членом у формі Лагранжа.
, де с є (х0,х) є формулою Тейлора при n =0 із залишковим членом у формі Лагранжа.
Якщо х0=0, то формула Тейлора називається ще формулою Маклорена:
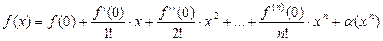 , де
, де  – нескінченно мала вищого порядку ніж
– нескінченно мала вищого порядку ніж 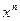 при
при  . Залишковий член
. Залишковий член  можна виписати точніше
можна виписати точніше 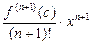 , де точка с належить інтервалу з кінцями 0 та х.
, де точка с належить інтервалу з кінцями 0 та х.
Формули Тейлора, Маклорена є незамінними для наближених обчислень з наперед заданою точністю. Детальніше з ними познайомимось, вивчаючи тему «Ряди».
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 2502; Нарушение авторских прав?; Мы поможем в написании вашей работы!