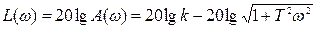Безінерційна ланка

ТИПОВІ ДИНАМІЧНІ ЛАНКИ БЕЗПЕРЕРВНИХ САУ ТА ЇХ ХАРАКТЕРИСТИКИ

Чим докладніше математична модель САК, тим вище порядок n її диференціального рівняння. Передавальні функції систем високого порядку (зазвичай n > 4) виявляються громіздкими і незручними для аналізу. Щоб вийти з цього положення, передавальну функцію представляють у вигляді перемноження простих співмножників, порядок яких не перевищує два. Такі співмножники називають типовими ланками.

Безінерційна (статична) ланка є найпростішою серед всіх типових ланок. Вона передає сигнал з входу на вихід миттєво, без спотворення його форми. У ланці може відбуватися тільки посилення або послаблення вхідного сигналу.

Зв'язок між миттєвими значеннями вхідної величини x(t) і вихідної величини у(t) описується рівнянням алгебри:

y(t) = kx(t).

Передавальні властивості ланки визначаються лише одним параметром - коефіцієнтом передачі k.

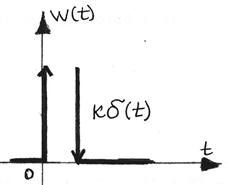
Перехідна функція Імпульсна перехідна функція

h(t) = k1(t) w(t) = kd(t)

Рівняння ланки в операційній формі Y(p) = kX(p)

Передаточна функція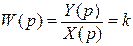

A(w) = |W(jw)| = k 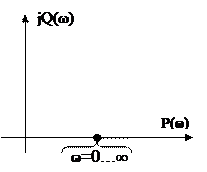j(w) = arctg(0/R) = 0 W(jw) = k

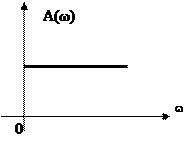
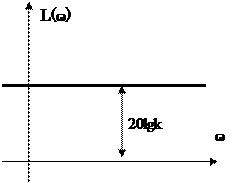L(w) = 20 lg A(w) = 20 lg k

АЧХ і ФЧХ безінерційної ланки показують, що сигнали будь-якої частоти (0; +¥) проходять через ланку з однаковим відношенням амплітуд вихідної і вхідної величини, рівним k і не мають між собою фазового зсуву.

Прикладами безінерційних ланок є редуктор, датчик потенціометра кутового переміщення, тахогенератор, який використовують як датчик частоти обертання і т. д. Пропорційними ланками моделюються підсилювачі, редуктори, дільники напруги і т. п.

Слід зазначити, що поняття безінерційної ланки є продуктом математичної ідеалізації. Насправді всі реальні конструктивні елементи САК володіють деякою інерційністю, оскільки передача енергії з входу на вихід елементу не може здійснюватися миттєво. Проте, якщо інерційність того або іншого елементу на два-три порядки менша, ніж у решти елементів даної системи, то його вважають безінерційною ланкою.

5.2. Інерційна ланка першого порядку (аперіодична ланка)

Фізично аперіодична ланка містить один елемент, що накопичує енергію, а також один або декілька елементів здатних її розсіювати.

Диференціальне рівняння:

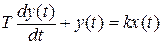
k – коефіцієнт передачі, характеризує властивості ланки в статичному режимі.

Т – постійна часу, характеризує інерційність ланки

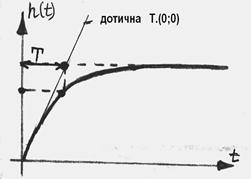
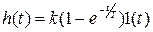
Коефіцієнт посилення ланки визначає рівень, до якого прагне перехідна характеристика з часом. Дотична, проведена на початку координат до перехідної характеристики, перетинає цей рівень у момент часу, рівний постійної часу аперіодичної ланки Т. Ці властивості аперіодичної ланки, а також те, що перехідний процес закінчується приблизно за час, що дорівнює 3Т, дозволяє визначати параметри ланки (коефіцієнт посилення і постійну часу) по його експериментальній перехідній характеристиці.

Рівняння ланки в операторній формі (Tp+1)Y(p) = kX(p)

Передаточна функція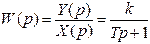

АФ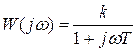ЧХ: АЧХ: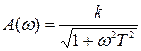

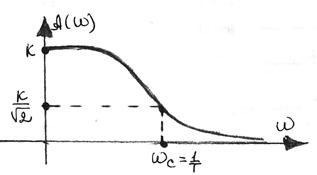
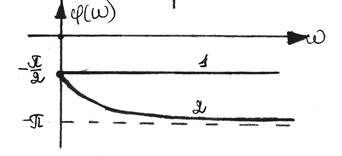
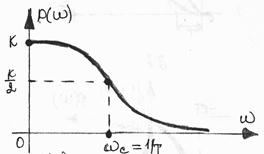
Аналізуючи графік функції , видно, що гармонійні сигнали малої частоти () пропускаються ланкою добре - з відношенням амплітуд вихідної і вхідної величин, близьким до передавального коефіцієнта k. Сигнали великої частоти (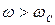) погано пропускаються ланкою: відношення амплітуд істотно менше коефіцієнта k. Чим більше постійна часу Т, тобто чим більше інерційність ланки, тим менше АЧХ витягнута уздовж осі частот, або, як прийнято говорити в ТАУ, тим вужче смуга пропускання частот. Таким чином, інерційна ланка першого порядку по своїх частотних властивостях є фільтром низької частоти.

ФЧХ:

ВЧХ:

	МЧХ:
		ЛАЧХ:

У практичних розрахунках використовують наближену або асимптотичну характеристику , яка є ламана у вигляді двох асимптот.

Першу асимптоту (низькочастотна) маємо при низьких частотах, коли величиною у виразі можна нехтувати і прийняти, що 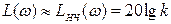. Низькочастотна асимптота від частоти не залежить і є прямою, паралельною осі частот і віддалену від неї на відстані .

Друга асимптота (високочастотна) замінює точну характеристику при великих частотах, коли 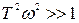, і одиницю під коренем у виразі можна не враховувати. Вираз для цієї асимптоти має вигляд: .

Ця асимптота залежить від частоти. У логарифмічній системі координат вона є прямою, що має негативний нахил і що проходить через точку з координатами , 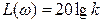. Приріст високочастотної асимптоти, що приходить на одну декаду, рівний -20 дб.

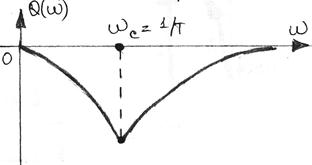
Значення сполучної частоти при якій перетинаються обидві асимптоти, знайдемо з умови 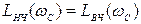, звідки .

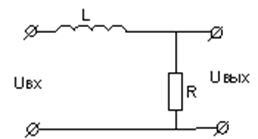Інерційними ланками першого порядку є конструктивні елементи, які можуть накопичувати і передавати енергію або речовину. У електричних елементах накопичувачем енергії електричного поля служить конденсатор, а магнітного поля - індуктивність. У механічних елементах потенційна енергія накопичується в пружинах і інших пружних елементах, а кінетична - в рухомих масах.

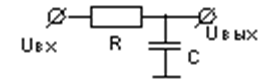
k = 1 T = RC k = 1 T = L/R

Дата добавления: 2014-01-07