Частотні характеристики

Частотні характеристики описують передавальні властивості елементів і системи в режимі усталених гармонійних коливань, викликаних зовнішнім гармонійним впливом. Частотні характеристики широко використовуються в теорії і практиці автоматичного керування, оскільки реальні збурення, що діють на САК, можуть бути представлені як сума гармонійних сигналів.

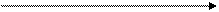
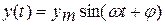
Для исследования частотных свойств системы и получения ее частотных характеристик на вход системы подают гармоническое воздействие определенной частоты 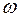и амплитуды X_m:

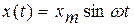
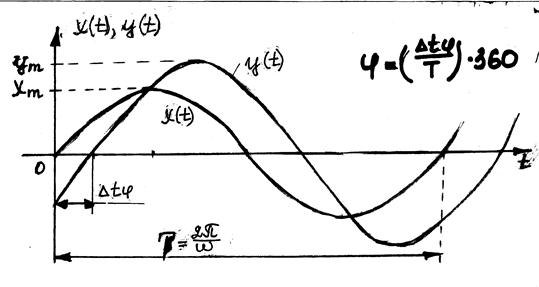
Після закінчення перехідного процесу елемент увійде до режиму усталених вимушених коливань, а вихідна величина у(t) змінюватиметься по гармонійному закону з тією ж частотою w, але з іншою амплітудою y_m, і зі зсувом 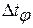по осі часу:

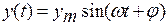
де 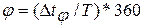- фазове зсув між вхідним і вихідним сигналами.

Повторюючи такий експеримент при фіксованому X_m для різних значень частоти (від 0 до 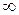), можна встановити, що амплітуда y_m і фазовий зсув j вихідного сигналу елемента залежать від частоти впливу. Подаючи гармонійний вплив на вхід різних елементів, можна переконатися, що величини y_m і j залежать також від типу і параметрів елементу. Отже, залежності амплітуди y_m і зсуву j від значень частоти w можуть служити характеристиками динамічних властивостей елементів.

Залежність відношення амплітуд вихідного і вхідного сигналів від частоти називають амплітудною частотною характеристикою (скорочено - АЧХ) і позначають A(w).

Залежність фазового зсуву між вхідним і вихідним сигналами від частоти називають фазовою частотною характеристикою (скорочено - ФЧХ) і позначають j (w).

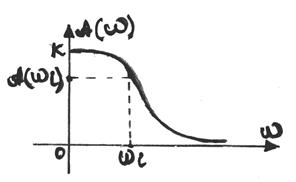
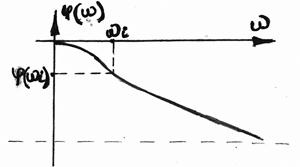
АЧХ показує, як елемент пропускає сигнали різної частоти. Оцінка пропускання проводиться по відношенню амплітуд y_m/x_m. ФЧХ показує, яке відставання або випередження вихідного сигналу по фазі створює елемент на різних частотах.

Амплітудну і фазову частотну характеристику можна об'єднати в одну загальну - амплитудно-фазову частотну характеристику (АФЧХ або АФХ). АФЧХ W( jw) є функцією комплексної змінної jw, модуль якої дорівнює A(w), а аргумент рівний j(w). Кожному фіксованому значенню частоти w _i відповідає комплексне число W(jw_i), яке на комплексній площині можна зобразити вектором, що має довжину А(w_i) і кут повороту j(w _i).

При зміні частоти від нуля до нескінченості вектор W(jw) повертається навколо початку координат, при цьому одночасно збільшується або зменшується довжина вектора. Кожній точці характеристики відповідає певне значення частоти.

Проекції вектора W(jw) на дійсну і уявну осі називають відповідно дійсною P(w) і уявною Q(w) частотними характеристиками.

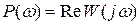
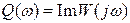
Дійсна частотна характеристика P(w) - завжди парна функція частоти, уявна Q(w) - завжди непарна функція.

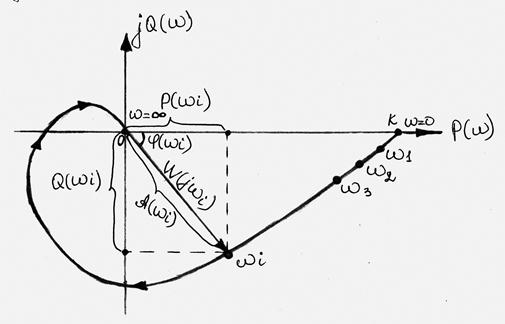
Аналітичний вираз для АФЧХ можна отримати з передавальної функції шляхом підстановки р = jw:

W(jw) =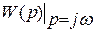

АФЧХ W(jw) може бути представлена:

- в показовій формі W(jw) = А(w)е^jj(w)

- в алгебраїчній W(jw) = P(w) + jQ(w)

- у тригонометричній W(jw) = A(w)cosj(w) + jA(w)sinj(w)

Зв'язок між різними частотними характеристиками:

А(w) = |W(jw)| =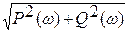

j(w) = argW(jw) =

При практичних розрахунках САК зручно використовувати частотні характеристики, побудовані в логарифмічній системі координат. Такі характеристики називають логарифмічними. Вони мають меншу кривизну і тому можуть бути наближено, замінені ламаними лініями, складеними з декількох прямолінійних відрізків. До того ж, ці відрізки в більшості випадків вдається побудувати без громіздких обчислень за допомогою деяких простих правил. Крім того, в логарифмічній системі координат легко знаходити характеристики різних з'єднань елементів, оскільки множенню і діленню звичайних характеристик відповідає складання і віднімання ординат логарифмічних характеристик.

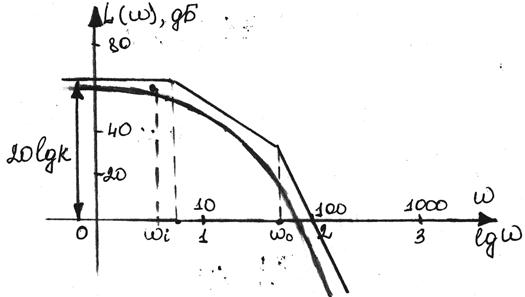
За одиницю довжини по осі частоти логарифмічних характеристик принимають декаду. Декада - інтервал частот, ув'язнений між довільним значенням w_i і його десятиразовим значенням 10*w_i. Відрізок логарифмічної осі частот, що відповідає одній декаді, дорівнює 1.

Логарифмічна амплітудна частотна характеристика ЛАЧХ:

L(w) = 20lgA(w).

Ординати ЛАЧХ вимірюються в белах (Б) або децибелах (дБ).

Бел - одиниця вимірювання відношення потужностей двох сигналів.

Якщо потужність одного сигналу більше (менше) потужності іншого сигналу в 10 разів, то ці потужності відрізняються на 1 Б. Оскільки потужність гармонійного сигналу пропорційна квадрату його амплітуди, то при застосуванні цієї одиниці для вимірювання відношення амплітуд перед логарифмом з'являється множник 2.

Дата добавления: 2014-01-07