Операторний метод. Передавальна функція

Найбільш поширеним методом опису автоматичних систем є операторний метод (метод операційного числення). У основі методу лежить перетворення Лапласа:

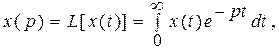
яке встановлює відповідність між функціями дійсної змінної t і функціями комплексного змінного р. Функцію часу x(t), що входить в інтеграл Лапласа називають оригіналом, а результат інтеграції - функцію x(p) - зображенням функції x(t) по Лапласу.

Перетворення Лапласа здійснюється лише для таких функцій часу, які дорівнюють нулю при t < 0. Ця умова забезпечується зазвичай множенням функції x(t) на одиничну стрибкоподібну функцію 1(t). З математичної і фізичної точок зору такий штучний прийом коректний, оскільки функції x(t) описують процеси в автоматичних системах, що починаються з деякого моменту часу, а цей момент часу завжди можна вважати початком відліку.

Для знаходження зображень по Лапласу різних функцій існую довідкові таблиці.

Основні властивості перетворення Лапласа приведені в таблиці.

Властивість	Оригінал	Зображення
Лінійність	ax(t) x1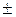(t)x2(t)	aX(p) X1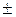(p)X2(p)
Правило диференціювання (за нульових початкових умов)		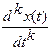X(p)*p^k
Правило інтеграції (за нульових початкових умов)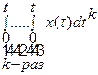
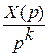
Зміна масштабу часу (теорема подібності)		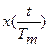X(pTm)*Tm
Зсув аргументу оригіналу (теорема запізнювання)
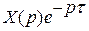
Теорема про початкове значення оригіналу
Теорема про кінцеве значення оригіналу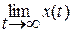

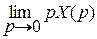
Найбільш важливими властивостями перетворення Лапласа є наступні правила:

при нульових початкових умовах диференціюванню оригіналу x(t) по

змінною t відповідає перемноження зображення X(p) на комплексну

змінну p, а інтеграції оригіналу відповідає ділення X(p) на р.

Широке розповсюдження операційного методу в ТАУ обумовлене тим, що з його допомогою визначають передавальну функцію, яка є найкомпактнішою формою опису динамічних властивостей елементів і систем.

Застосуємо перетворення Лапласа до лінійного диференціального рівняння (2), вважаючи, що до застосування зовнішнього впливу система знаходилася у спокої і всі початкові умови дорівнюють нулю. Використовуючи властивість лінійності і правило диференціювання, можна отримати рівняння алгебри в зображеннях:

D(p)Y(p) = K(p)X(p) (3)

де D(p) = a₀pⁿ+a₁p^n-1+….+a_n – власний оператор

K(p) = b₀p^m+b₁p^m-1+…+b_m – вхідний оператор

Рівняння (3) отримане із рівняння (1) з використанням наступної заміни оригіналів зображеннями:

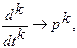y(t)=Y(p), x(t)=X(p)

Передавальною функцією W(p) називають відношення зображення по Лапласу вихідної величини до зображення вхідної величини при нульових початкових умовах

Для системи, що описується рівнянням (2), передавальна функція є деяким динамічним оператором, що характеризує проходження сигналів через лінійний елемент і незалежний від виду вхідного впливу x(t), і характеризує лише власні динамічні властивості описуваного елементу або системи.

Передавальну функцію формально можна отримати з диференціального рівняння шляхом заміни в ньому символу кратного диференціювання на відповідний степінь p і ділення утвореного таким чином багаточлена правої частини рівняння на багаточлен лівої частини.

Основні властивості і особливості передавальної функції САУ.

1. Передавальна функція встановлює зв'язок між вхідною і вихідною величиною, як в динамічному, так і в статичному режимах.

2. Передавальна функція реальних елементів - правильний раціональний дріб, у якого ступінь багаточлена чисельника менше або дорівнює ступеню багаточлена знаменника.

3. Всі коефіцієнти передавальної функції - дійсні числа, що характеризують параметри елементу або системи.

4. Передавальна функція є функцією комплексної змінної яка при деяких значеннях змінної p може звертатися в нуль або нескінченність. Значення змінної p, при якому функція W(p) звертається в нуль, називають нулем, а при якому звертається в нескінченність - полюсом передавальної функції. Нулі передавальної функції - корені полінома K(p), полюси - корені полінома D(p). Корені поліномів чисельника і знаменника можуть бути комплексним, уявними і дійсними. Якщо ці корені відомі, то передавальна функція може бути представлена у вигляді:

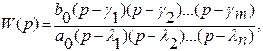
де - корені багаточлена K(p) (нулі W(p));

- корені багаточлена D(p) (полюса W(p)).

5. Передавальна функція елементу пов'язана з його імпульсною перехідною функцією перетворенням Лапласа:

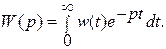
Дата добавления: 2014-01-07