Z-преобразование

Z-преобразование связано дискретным преобразованием Лапласа посредством подстановки .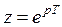

Z-преобразованием решетчатой функции называется функция комплексного аргумента z, определяемая выражением

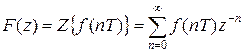
для смещенной решетчатой функции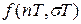

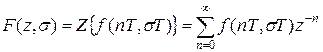
Главное достоинство и удобство z -преобразования заключается в том, что сама запись z -изображения указывает простой способ выполнения прямого и обратного преобразования:

- чтобы по известной функции времени 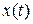найти ее z -изображение, необходимо лишь каждое дискретное значение умножить на , а затем свернуть получившийся степенной ряд в конечную сумму;

- чтобы по известному изображению найти соответствующий сигнал 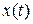, необходимо представить изображение в виде степенного ряда по убывающим степеням , получающиеся при этом числовые коэффициенты ряда и есть дискретные значения сигнала .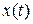

Основные свойства Z-преобразования

1. Свойство линейности

,

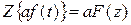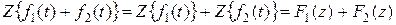
а – постоянный коэффициент.

Здесь и далее .

2. Теорема сдвига во временной области (теорема запаздывания и упреждения)

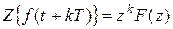
3. Теорема об умножении оригинала на экспоненту (теорема смещения в области изображений)

, ;

, ;

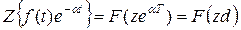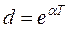для смещенной решетчатой функции

, ;

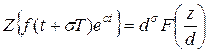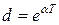4. Теорема об умножении оригинала на степенную функцию

.

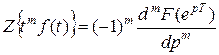5. Теорема о конечном значении оригинала

.

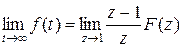6. Теорема о начальном значении оригинала

.

7. Изображение разностей. На основании формул теоремы сдвига во временной области изображение первой разности имеет вид

Для k-той разности

, .

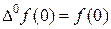8. Изображение сумм.

Аналогами интеграла непрерывной функции в пределах от 0 до t для решетчатой являются неполная сумма и полная сумма:

,

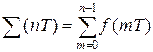Z – изображение неполной суммы

,

Z – изображение полной суммы

.

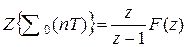Для случая k-кратного суммирования

,

9. Свертка решетчатых функций.

Есл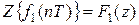и и ,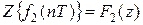

то

и .

Дата добавления: 2014-01-07