Синтез непрерывных корректирующих устройств в дискретных системах

В случае непрерывной коррекции, корректирующие устройства изменяют характеристики непрерывной части дискретной системы. Различные варианты включения корректирующих устройств приведены на рисунке 26.11.

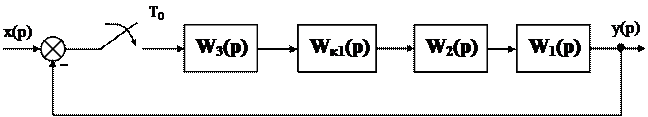Рисунок 26.11 Структурные схемы дискретных систем с непрерывными корректирующими устройствами

Наиболее просто производится расчет корректирующих средств последовательного типа. В этом случае дискретная передаточная функция разомкнутой системы должна равняться желаемой передаточной функции

.

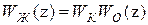Здесь 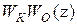представляет собой дискретную передаточную функцию последовательно включенных корректирующего звена с передаточной функцией 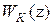и непрерывной части с передаточной функцией 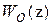. Напомним, что 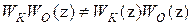. Поэтому расчет последовательных корректирующих средств в дискретных системах не является столь простой задачей, как в непрерывных системах.

Однако выше было показано, что ЛАЧХ дискретных систем, построенные в функции абсолютной псевдочастоты 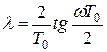для частот 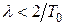практически сливаются с ЛАЧХ непрерывной части. Поэтому можно воспользоваться известными приемами расчета последовательных корректирующих средств, если в качестве желаемых ЛАЧХ использовать характеристики, соответствующие передаточным, функциям непрерывной части.

Требуемый вид последовательного корректирующего звена определяется в этом случае по виду ЛАЧХ, полученной вычитанием ординат ЛАЧХ нескорректированной системы из ординат желаемой (типовой) ЛАЧХ.

Пример 26.3. Произведем расчет системы с астатизмом первого порядка по следующим исходным данным: максимальная скорость слежения Ω_max= 20 град/сек; максимальное ускорение слежения 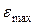= 10 град/сек²; максимальная допустимая ошибка 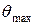= 4 угл. мин.; допустимый показатель колебательности M = 1,5; период дискретности сек; передаточная функция непрерывной части имеет вид

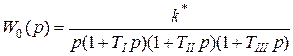
где T_I = 0,05 сек, T_II = 0,003 сек, T_III = 0,001 сек.

Определим вид и параметры последовательного корректирующего звена, которое должно быть включено в непрерывную часть системы, а также необходимое значение общего коэффициента усиления k*.

Левее частоты среза ЛАЧХ дискретной системы совпадает с ЛАЧХ ее непрерывной части, а псевдочастота 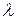- с реальной частотой 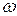. Поэтому формирование желаемой ЛАЧХ левее частоты среза произведем обычными приемами.

Построим запретную зону для ЛАЧХ из условий точности (рис. 26.12).

Контрольная частота 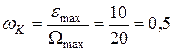сек^-1

Модуль передаточной функции разомкнутой системы при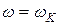

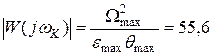дБ

По этим данным на рис.26.12 построены контрольная точка А_к и запретная зона, сформированная из прямых с наклоном -20 и -40 дБ/дек (наклоны 1 и 2).

Желаемая ЛАЧХ в низкочастотной области формируется так, чтобы она проходила выше точки А_к на 3 дБ. Она состоит из отрезков прямых с наклонами 1-2-1. В низкочастотной области частотная передаточная функция разомкнутой системы имеет вид

.

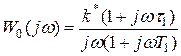Параметры желаемой ЛАЧХ и передаточной функции разомкнутой системы в низкочастотной области определим в следующем порядке. Базовая частота ЛАЧХ

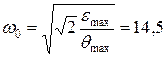сек^-1

Постоянная времени корректирующего звена, формирующая первый излом ЛАЧХ:

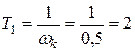сек.

Для получения заданного показателя колебательности должно выдерживаться условие:

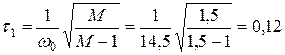сек.

Далее определяем необходимое значение общего коэффициента усиления:

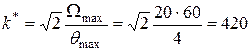сек.^-1

и частоту среза ЛАЧХ:

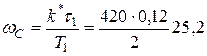сек^-1.

Для обеспечения заданного показателя колебательности в высокочастотной области должно удовлетворяться неравенство:

,

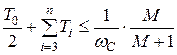где 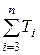- сумма постоянных времени меньших, чем .

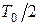Отсюда получаем допустимое значение для суммы постоянных времени:

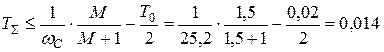сек.

На рис. 26.12 пунктиром построена ЛАЧХ непрерывной части нескорректированной системы, сплошной линией - желаемая (скорректированная) ЛАЧХ непрерывной части. В низкочастотной области (до частоты среза 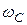) она совпадает с ЛАЧХ дискретной системы. В области высоких частот вид желаемой ЛАЧХ непрерывной части, вообще говоря, может быть произвольным. Важно только, чтобы сумма постоянных времени 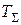не превышала допустимого значения.

Наиболее простые корректирующие звенья получаются в тех случаях, когда сопрягающие частоты ЛАЧХ нескорректированной системы и желаемой ЛАЧХ совпадают между собой. В рассматриваемом примере

.

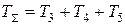Целесообразно принять 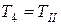= 0,003 сек, 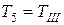= 0,001 сек.

Тогда 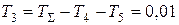сек.

Вычитая из ординат желаемой ЛАЧХ ординаты характеристики нескорректированной системы, получим искомую ЛАЧХ. последовательного корректирующего звена. Она соответствует интегро - дифференцирующему звену с передаточной функцией

.

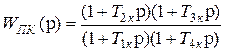где

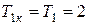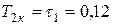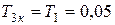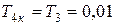сек, сек, сек, сек.

Из приведенного примера 26.3 видно, что при синтезе непрерывных последовательных корректирующих устройств метод логарифмических частотных характеристик не теряет своей простоты и наглядности.

Можно показать, что при наличии временного запаздывания допустимый период повторения ЦВМ должен быть снижен в соответствии с формулой

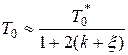, (26.6)

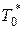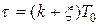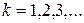где - допустимый период повторения, полученный в результате синтеза системы без учета запаздывания. Время запаздывания , где и .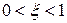

Если время запаздывания соответствует целому числу периодов, то формула (26.6) становится точной:

.

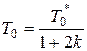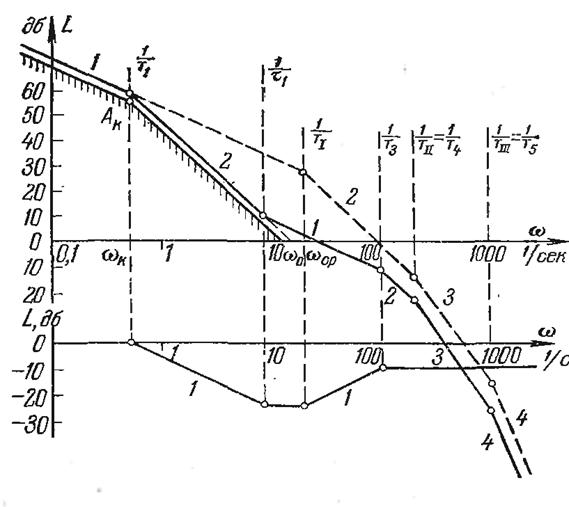
Рисунок 26.12. Построение желаемой ЛАЧХ

Дата добавления: 2014-01-07