Комбинированное регулирование

В цифровых системах возможно использование комбинированного регулирования по задающему или возмущающему воздействиям. При выполнении заданных условий по точности комбинированное регулирование позволяет снизить требования к основному каналу.

Комбинированное регулирование особенно удобно применять в тех случаях, когда задающее воздействие вычисляется в управляющей ЦВМ. В этом случае на ЦВМ может быть также возложена задача вычисления производных этого воздействия, что позволяет просто реализовать схемы комбинированного регулирования, аналогичные применяемым в непрерывных системах. Подобное положение возникает, например, при слежении телескопов за планетами, при управлении по вычисляемым координатам и т. п.

Структурная схема системы комбинированного регулирования для случая использования дополнительного канала с передаточной функцией по задающему воздействию изображена на рис. 26.16.

Рисунок 26.16. Структурная схема системы комбинированного регулирования

Эквивалентная передаточная функция замкнутой системы с учетом дополнительного канала

,

где - передаточная функция разомкнутой системы,

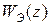- эквивалентная передаточная функция разомкнутой системы.

Эквивалентная передаточная функция по ошибке

. (26.11)

Эквивалентная передаточная функция разомкнутой системы

Из формулы (26.11), если положить 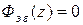, можно получить условие полной инвариантности

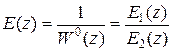(26.12)

Для большинства реальных систем степень числителя 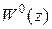оказывается меньше степени знаменателя на единицу. Поэтому степень полинома будет на единицу больше степени полинома и формула (26.12) может быть приведена к виду

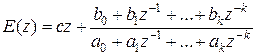. (26.13)

Слагаемое 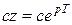означает, что при формировании сигнала по каналу с передаточной функцией необходимо использовать упрежденное на один такт значение задающего воздействия. Это связано с необходимостью применения прямых разностей, которые в дискретном плане должны здесь заменить процесс дифференцирования. При этом возможны следующие ситуации.

1. Если ЦВМ вычисляет значение задающей величины по некоторым заложенным в нее данным и использует при этом прогнозирование (например, при вычислении текущих координат небесных тел, спутников, ракет и др.), то вычисление будущего значения интересующей величины может быть легко сделано со сдвигом на практически любое число тактов. В этом случае реализация формулы (26.13) в принципе возможна. Однако практические трудности в реализации слишком сложных алгоритмов и ограничения в элементах не дают возможности получить полную инвариантность.

2. Если ЦВМ вычисляет задающую величину не по принципу прогнозирования, а в результате обработки поступающей текущей информации, то точная реализация формулы (26.13) оказывается невозможной. Тогда приходится ограничиться приближенной реализацией формулы (26.12) либо вводить в прямой канал дополнительное запаздывание на один такт. В первом случае условие полной инвариантности (26.13) нарушается, во втором - вводится постоянное временное запаздывание на один такт в обработку задающего воздействия, что также нарушает условие инвариантности.

Таким образом, при использовании комбинированного регулирования приходится ориентироваться не на полную инвариантность, а на некоторое, во многих случаях весьма существенное, повышение точности.

Поскольку точность систем регулирования определяется низкочастотной частью ЛАЧХ, а низкочастотная часть ЛАЧХ дискретных систем практически сливается с ЛАЧХ непрерывной части системы, то расчет дискретных систем комбинированного регулирования осуществляется аналогично непрерывному случаю.

Важнейшим следствием использования комбинированного регулирования является возможность снижения требований к ЦВМ в части ограничения периода дискретности. Это связано с понижением требований к каналу регулирования по отклонению при введении дополнительного канала с передаточной функцией .

Пониженные требования к точности воспроизведения в канале регулирования по отклонению позволяют перейти к желаемым ЛАЧХ с меньшим значением частоты среза. Это дает возможность увеличить период дискретности Т₀ при сохранении необходимого запаса устойчивости.

ПЕРЕЛІК РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ

1. Теория автоматического управления / Под ред. А.А.Воронова - М.: Высшая школа, 1986, ч. 1, 2.

2. Теория автоматического управления / Под ред. А.В.Нетушила - М.: Высшая школа, 1983. – 432 с.

3. Попов Е.П. Теория нелинейных систем автоматического регулирования и управления. М.: Наука, 1988. 304 с.

4. Зайцев Г.Ф., Стеклов В.К., Бріцький О.І. Теорія автоматичного управління. - К., Техніка, 2002.- 688 с.

5. Попович М.Г., Ковальчук О.В. Теорія автоматичного керування. Підручник. – Київ: Либідь, 1997. – 544с.

6. Лукас В. А. Теория автоматического управления. – М.: Недра, 1990. – 416 с.

7. Зайцев Г.Ф. Теория автоматического управления и регулирования. Киев: Вища школа, 1988 - 431 с.

Навчальне видання

Конспект лекцій з курсу

"Теорія автоматичного управління"

Частина 2 – Нелінійні та дискретні САУ

Для студентів, що навчаються за напрямом

6.050201“Системна інженерія” (СУА)

(для денної й заочної форм навчання)

Укладач: Федюн Роман Валерійович, к.т.н, доц.

Рецензент Секірін Олександр Іванович, к.т.н, доц.

Відповідальний

за випуск Бессараб Володимир Іванович, к.т.н., доц., зав. каф.

Дата добавления: 2014-01-07