Теореми додавання

Теореми додавання і множення ймовірностей

Теорема 1.

Нехай подія А є сумою двох подій В та С, тоді

А) якщо події В та С несумісні, то

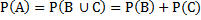
Б)якщо події В та С сумісні, то

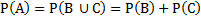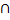– Р(В С)

Теорема 2

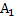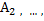
Нехай випадкові події , 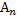попарно несумісні (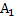несумісна з жодною іншою), тоді імовірність об’єднання дорівнює сумі імовірностей.

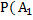
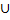
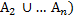= P(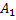) + P(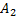) + … + P()

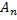Теорема 3

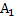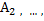
Якщо , 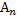утворюють повну групу, тоді

P(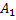) + P(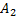) + … + P(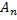) = 1

Наслідок:

Оскільки події А та 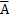утворюють повну групу, то Р(А) + Р(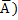= 1

Р(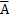) = 1- Р(А) – формула знаходження імовірності протилежної події.

Приклад 4

У відрі 25 троянд білого та червоного кольору. Червоних в 4 рази більше ніж білих. Яка імовірність того, що 2 навмання взяті троянди виявляться одного кольору

Х- кількість білих троянд, тоді кількість червоних Х +4Х= 25 Х=5

Білих троянд – 5

Червоних – 20

Подія А- дві білі троянди

Подія В- дві червоні троянди.

А і В несумісні події.

Р(А+В)=Р(А) + Р(В)

n =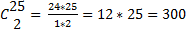

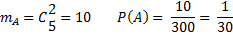
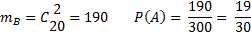
Р(А+В)=Р(А) + Р(В)=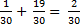

2.2 Теореми множення ймовірностей

Означення 1

Випадкові події В та С називаються залежними, якщо імовірність однієї з них змінюється залежно від того відбулася друга подія чи ні,в протилежному випадку події називають незалежними.

Означення 2

Імовірність події С визначають за умови, що відбулася подія В називається умовною. Позначають

P(C / B)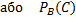

Теорема 4

Нехай подія А є добутком двох подій В та С, тоді

А) Якщо події В та С незалежні, то

Р(А)= Р(В*С)= Р(В) * Р(С) (5)

Б) Якщо події В та С залежні, тоді

Р(А)= Р(В*С)= Р(В) * Р(С/В) (6)

Ці теореми є вірними і для добутку n>2 подій.

Приклад 5

Маємо дві партії виробів. Перша партія – 8 стандартних і 2 нестандарні деталі. Друга – 7 стандартних і 3 нестандарні деталі. З кожної партії беруть по одному виробу. Знайти імовірність того, що вони обидва стандартні.

А- обидві стандартні.

В- 1 з першої стандартна

С- 1 з другої стандартна

Р(В)=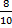

Р(С)=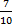

Події незалежні тому використовуємо формулу 5

Р(А)=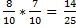

Приклад 6

В урні 7 білих і 3 чорні кульки. З урни витягають дві кулі. Знайти імовірність того, що дві кулі білі.

А- обидві кулі білі.

В- перша біла.

С- друга біла.

Р(В)=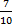

(С) =

Р(А)=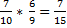

Дата добавления: 2014-01-07