Вступ до автоматного програмування

Автоматні моделі

Лекція 4

1. Вступ до автоматного програмування.

2. Автоматні моделі.

Відповідно до класифікації Д. Харела, будь-яку програмну систему можна віднести до одного з наступних класів:

· Трансформуючі системи здійснюють деяке перетворення вхідних даних, і після цього завершують свою роботу. У таких системах, як правило, вхідні дані повністю відомі і доступні на момент запуску системи, а вихідні - тільки після завершення її роботи. До трансформуючих систем відносяться, наприклад, архіватори й компілятори.

· Інтерактивні системи взаємодіють з навколишнім середовищем в режимі діалогу (наприклад, текстовий редактор). Характерною особливістю таких систем є те, що вони можуть контролювати швидкість взаємодії з навколишнім середовищем - змушувати середовище «чекати».

· Реактивні системи взаємодіють з навколишнім середовищем шляхом обміну повідомленнями в темпі, що задається середовищем. До цього класу можна віднести більшість телекомунікаційних систем, а також системи контролю та управління фізичними пристроями.

Скінченні автомати в програмуванні традиційно застосовуються при створенні компіляторів, які відносяться до класу трансформуючих систем. Автомат тут розуміється як певний обчислювальний пристрій, що має вхідну і вихідну стрічки. Перед початком роботи на вхідній стрічці записано рядок, який автомат далі посимвольно зчитує й обробляє. В результаті обробки автомат послідовно записує деякі символи на вихідну стрічку.

Інша традиційна область використання автоматів - завдання логічного управління - є підкласом реактивних систем. Тут автомат, на перший погляд, зовсім інший пристрій. У нього кілька паралельних входів (найчастіше двійкових), на які в режимі реального часу надходять сигнали від навколишнього середовища. Обробляючи ці сигнали, автомат формує значення декількох паралельних виходів.

Критерій застосовності автоматного підходу найкраще виражається через поняття «складна поведінка». Неформально можна сказати, що сутність (об'єкт, підсистема) володіє складною поведінкою, якщо в якості реакції на деяку вхідну дію вона може здійснити одну з декількох вихідних дій. При цьому істотно, що вибір конкретної вихідної дії може залежати не тільки від вхідної дії, але й від передісторії. Для сутностей з простою поведінкою реакція на будь-яку вхідну дію залежить тільки від цього впливу (рис.1).

Рис.1. Сутність з простою поведінкою (зліва) і складною поведінкою (справа)

Одна з центральних ідей автоматного програмування полягає в відділенні опису логіки поведінки (за яких умов необхідно виконати ті чи інші дії) від опису його семантики (власне сенсу кожної з дій). Крім того, опис логіки при автоматному підході жорстко структуровано. Ці властивості роблять автоматний опис складної поведінки наочним і зрозумілим.

Основна рекомендація по застосуванню автоматного програмування дуже проста: використовуйте автоматний підхід при створенні будь-якої програмної системи, в якій є сутності зі складною поведінкою. Досвід показує, що такою властивістю володіє практично будь-яка серйозна система. Проте зазвичай не всі компоненти системи характеризуються складною поведінкою. Тому дану вище рекомендацію можна доповнити ще однією: використовуйте автоматний підхід при створенні лише тих компонентів системи, які є сутностями зі складною поведінкою. Це доповнення закликає не перевантажувати специфікації й код описом логіки там, де в цьому немає необхідності.

Базовим поняттям автоматного програмування є «стан». Це поняття (в тому сенсі, як воно використовується в описуваної парадигмі) було введено А. Тюрінгом і з успіхом застосовується в багатьох інших галузях науки, наприклад, в теорії управління й теорії формальних мов.

Основна властивість стану системи в момент часу t0 полягає в «відділенні» майбутнього (t> t0) від минулого (t <t0) в тому сенсі, що поточний стан несе в собі всю інформацію про минуле системи, необхідну для визначення її реакції на будь-яку вхідну дію, сформовану в момент часу t0.

При використанні поняття «стан» знання передісторії більше не потрібно. Стан можна розглядати як особливу характеристику, яка в неявній формі об'єднує всі вхідні дії минулого, що впливають на реакцію сутності в даний момент часу. Реакція залежить тепер тільки від вхідної дії й поточного стану.

Найчастіше, вхідна дія - це вектор. Його компоненти підрозділяються на події та вхідні змінні в залежності від смислу і механізму формування. Сукупність скінченної множини станів і скінченної множини вхідних дій утворює (скінченний) автомат без виходів. Такий автомат реагує на вхідні дії, певним чином змінюючи поточний стан. Правила, за якими відбувається зміна станів, називають функцією переходів автомата.

Те, що в автоматному програмуванні власне і називається (скінченним) автоматом (рис.2), виходить, якщо поєднати поняття автомата без виходів з поняттям «вихідна дія». Такий автомат реагує на вхідний вплив не тільки зміною стану, але і формуванням певних значень на виходах. Правила формування вихідних дій називають функцією виходів автомата.

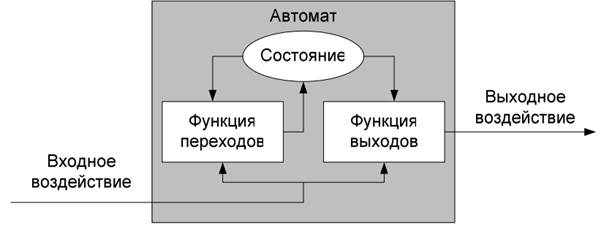
Рис.2. Скінченний автомат

Розглянемо спочатку один з абстрактних обчислювачів, що широко застосовуються у теорії формальних мов - машину Тюрінга. Ця абстрактна машина була запропонована А. Тюрінгом в 1936 р. в якості формального визначення поняття «алгоритм». Теза Черча-Тюрінга говорить, що все, що можна «вирахувати», «запрограмувати» або «розпізнати» в будь-якому сенсі (з формально визначених в даний час), можна обчислити, запрограмувати або розпізнати за допомогою підходящої машини Тюрінга.

Машина Тюрінга складається з двох частин: пристрою управління і запам'ятовуючого пристрою - стрічки (рис. 3). Стрічка містить безліч комірок, в яких можуть бути записані символи деякого скінченного алфавіту. У кожен момент часу на одній з комірок стрічки встановлена ​​голівка читання-запису, що дозволяє пристрою керування зчитувати або записувати символ в цій комірці.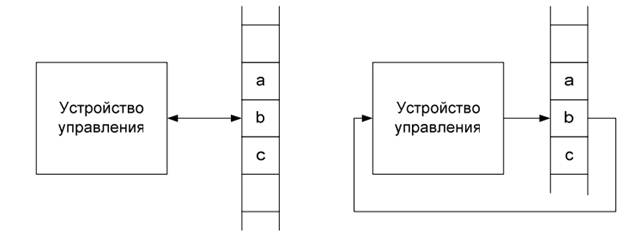

Рис.3. Машина Тюрінга: традиційне зображення (зліва) й зображення в традиціях теорії керування (справа)

Пристрій керування є скінченним автоматом. Він має єдину вхідну дію (символ, що зчитується зі стрічки) і дві вихідних дії (символ, що записується на стрічку, і вказівка ​​голівці зрушитися на одну комірку в ту чи іншу сторону, або залишитися на місці).

Теза Черча-Тюрінга означає, що в термінах операцій машини Тюрінга можна записати всі ті ж програми, що і на будь-якій існуючій мові програмування.

Наприклад, необхідно реалізувати функцію інкремента. Нехай початкове число записано на стрічці в двійковому вигляді зліва направо, у решті комірок знаходиться порожній символ ('blank') і голівка вказує на старший розряд числа. Тоді для збільшення числа на одиницю можна запропонувати наступний алгоритм:

1. Рухатися вправо, поки не зустрінеться порожній символ.

2. Зрушитися на одну комірку вліво.

3. Поки в поточній клітинці знаходиться символ '1 ', змінювати його на '0' і рухатися вліво.

4. Якщо в поточній клітинці знаходиться '0 'або' blank ', записати в комірку '1' і завершити роботу.

Цей алгоритм необхідно «ввести» («закодувати») в пристрій керування машини Тюрінга). Іншими словами, необхідно задати стани, а також функції переходів і виходів її керуючого автомата. Зручний і наочний спосіб зробити це надають графи переходів автоматів, які ще називаються діаграмами переходів. Вершини в цьому графі відповідають станам автомата, а дуги - переходам між станами. Кожна дуга позначається умовою переходу (значеннями вхідних дій, що ініціюють цей перехід) і дією на переході (значеннями вихідних дій).

На рис.4 представлено граф переходів керуючого автомата машини Тюрінга, що реалізує функцію інкремента. Тут символ 'b' скорочення від blank, символ '*' на місці записуваного символу означає «Записати той же самий символ, що було зчитано». Команди голівці позначаються стрілками (стрілка вниз означає «Залишитися на місці»). У мітці переходу над рискою записується його умова, а під рискою – дія.

Рис.4. Збільшення числа на одиницю за допомогою машини Тюрінга

У графі переходів позначені імена станів керуючого автомата. Ці імена відображають смисл стану і є коротким описом поведінки машини в цьому стані.

Отже, керуючий автоматом машини Тюрінга, що реалізує функцію інкремента, має три стани. Скільки ж станів у цієї машини в цілому? Її дії в кожен момент часу повністю визначаються сукупністю стану керуючого автомата, рядка на стрічці та положення голівки. Відзначимо, що символи на стрічці для пристрою управління являють собою вхідні дії, однак, щодо машини в цілому вони не є вхідними (зовнішніми), а формують частину внутрішнього стану обчислювача. Всіляких рядків на стрічці, як і положень головки, нескінченно багато, тому й у машини Тюрінга нескінченна кількість станів.

Проте, якщо замислитися, стану керуючого пристрою і стани стрічки мають принципово різні значення. У наведеному прикладі виявилося, що для того щоб задати алгоритм для машини Тюрінга, достатньо описати її поведінку в кожному з трьох станів керуючого автомата (рис.4). Нам не треба було задавати реакцію машини для кожної з безлічі можливих вхідних рядків. Неформально можна сказати, що стану керуючого автомата визначають дії машини, а стан стрічки - лише результат цих дій.

Тут доречна аналогія з об'єктно-орієнтованого програмування. Викликаючи компонент (метод) деякого класу, клієнт вказує ім'я компонента і, якщо потрібно, його фактичні аргументи. Різних компонентів в класі зазвичай всього декілька, в той час як різних аргументів може бути неосяжно багато. При цьому ім'я компоненту визначає дію (алгоритм обчислень), а значення аргументів - тільки результат дії (результат обчислень).

Очевидно, що стани пристрою керування та стани стрічки - зовсім різні поняття з точки зору програмування на машині Тюрінга, і змішувати їх не варто. Перші слід явно перераховувати, відображати на графі переходів, описувати алгоритм поведінки в кожному з них. Другі в програмі в явному вигляді не беруть участь, побудувати граф переходів між ними неможливо, а якщо б це і вдалося, то для розуміння програми такий граф не мав користі.

Перші можна назвати якісними станами машини, а другі - кількісними. В автоматному програмуванні для цих двох класів станів прийняті терміни, запозичені з теорії управління. Стани автомата називаються керуючими, а стани стрічки - обчислювальними.

Таблиця 1. Керуючі й обчислювальні стани

Керуючі стани	Обчислювальні стани
Їх кількість не дуже велика	Їх кількість або нескінченна, або скінченна, проте дуже велика
Кожен має визначений смисл і якісно відрізняється від інших	Більшість з них не має смислу і відрізняється від інших лише кількісно
Вони визначають дії, що виконує сутність	Вони безпосередньо визначають лише результати дій

Перехід від стрічки, голівки й найпростіших команд до мов високого рівня, звичайно, спрощує програмування, але при реалізації сутностей зі складною поведінкою повністю проблеми не вирішує. Досвід розгляду машини Тюрінга підказує, що для того, щоб зробити програму простою і зрозумілою, необхідно явно виділити керуючі стани (ідентифікувати їх, дати їм імена) та описати поведінку сутності в кожному з них.

Наприклад, при реалізації електронних годинників з будильником можна виділити три керуючих стани: «Будильник вимкнений», «Установка часу будильника» і «Будильник увімкнено». У кожному з цих станів реакція будильника на натискання будь-якої кнопки буде однозначною і специфічною.

У випадку з машиною Тюрінга виділення керуючих станів тривіальне, оскільки логіка в ній апріорі винесена в окремий пристрій - керуючий автомат. Подібна ідея використовується при побудові систем автоматизації, у яких завжди виділяють керуючі пристрої й керовані об'єкти. Дотримуючись цієї концепції, сутність зі складною поведінкою природно розділити на дві частини:

· керуючу частину, відповідальну за логіку поведінки - вибір виконуваних дій, що залежить від поточного стану й вхідної дії, а також за перехід у новий стан;

· керовану частину, відповідальну за виконання дій, обраних для виконання керуючою частиною, й, можливо, за формування деяких компонентів вхідних дій для керуючої частини - зворотних зв'язків.

У відповідно до традиції теорії керування, керована частина тут і далі називається об'єкт управління, а керуюча частина - система управління. Оскільки для реалізації керуючої частини використовуються автомати, то вона часто називається керуючий автомат або просто автомат.

Таким чином, відповідно до автоматного підходу, сутності зі складною поведінкою слід представляти у вигляді автоматизованих об'єктів управління - так в теорії управління називають об'єкт управління, інтегрований з системою управління в один пристрій.

Дата добавления: 2014-01-07