Автоматні моделі

В даний час запропоновані, досліджені й з успіхом застосовуються різні математичні моделі, в назвах яких використовується слово «автомат». Вони мають багато спільного в своїх основах, але відрізняються, часто істотно, в деталях. Причина різноманітності автоматних моделей пояснюється широтою сфери їх застосування.

Автомати є незамінним інструментом в таких далеких одна від одної областях як, наприклад:

· математична лінгвістика;

· логічне керування;

· моделювання поведінки людини;

· комунікаційні протоколи;

· теорія формальних мов, обчислюваності й обчислювальної складності.

Виявити спільне в різних автоматних моделях можна, якщо розглянути автомати як частинний випадок динамічних систем. Зазвичай терміном «динамічна система» в техніці, природі, житті й т. д. позначають систему, процеси якої розвиваються в часі. Стан системи в кожен момент часу характеризують деякою множиною узагальнених координат. Процеси в динамічній системі описуються рівняннями різних типів відносно узагальнених координат.

Динамічні системи можна розділити на кілька класів у залежності від наступних факторів.

· Модель часу. Час може вважатися таким, що тече безперервно або дискретно. У першому випадку час змінюється на континуумі, у другому – на зліченній множині, елементи якої називаються тактами.

· Розмірність системи. Кількість узагальнених координат може бути скінченним або зчисленним.

· Потужність множин координат. Кожна з узагальнених координат може приймати значення зі скінченної, або континуальної множини.

У фізиці й техніці часто використовуються системи, в яких час неперервний та узагальнені координати також змінюються на континуумі. Для опису процесів в таких системах використовуються диференційні рівняння. Якщо ж час дискретний, але узагальнені координати приймають значення з континуальних множин, то для опису процесів використовуються різницеві рівняння.

Ті системи, в яких час дискретний, кількість узагальнених координат скінченна й кожна координата може приймати значення зі скінченої множини, називають скінченними динамічними системами. Скінченні автомати належать до класу скінченних динамічних систем.

У теорії формальних мов вивчаються, так звані, абстрактні автомати (абстрактні машини, абстрактні обчислювачі). Внутрішня структура абстрактних автоматів не розкривається. Інтерес при їх вивченні представляє тільки обчислювальна потужність - клас мов, які може розпізнавати машина.

У логічному управлінні розглядаються структурні автомати. Вони виступають у ролі керуючих пристроїв в системах керування. Інтерес тут представляє кількість паралельних входів і виходів автомата, його зв'язку з об'єктом керування та іншими елементами системи, простота реалізації.

Автоматне програмування, з одного боку, об'єднує в собі досвід двох зазначених розділів теорії автоматів, а з іншого - є абсолютно самостійною областю. При використанні автоматів у програмуванні не мають значення ні дослідження обчислювальної потужності, ні, наприклад, мінімізація числа станів. У цій області нас цікавить тільки те, як використовувати скінченні автомати для побудови коректних програм.

Абстрактні скінченні автомати прийнято описувати в наступних термінах. Задана скінченна множина символів X, що називається (вхідним) алфавітом. Множина всіх можливих ланцюжків (послідовностей, рядків, слів), складених із символів алфавіту X позначається Х*. Порожня послідовність символів позначається ε, ε ∈ Х*. Підмножина L множини всіх ланцюжків над алфавітом X, L ⊂ Х*, називається мовою. Розглядається наступна проблема: задано мову L ⊂ Х * та ланцюжок ξ ∈ Х*. Визначити, чи належить ланцюжок мові (ξ ∈ L)?

Якщо абстрактний обчислювач здатний вирішити цю проблему для певної мови L ⊂ Х* та довільного рядка ε ∈ Х*, то говорять, що обчислювач розпізнає мову L. Таким чином, абстрактні автомати описуються в термінах тих мов, що вони розпізнають. Різні автоматні моделі можуть розпізнавати різні класи мов або, іншими словами, володіють різною обчислювальною потужністю (обчислювальна потужність моделі абстрактних автоматів тим більше, чим ширше клас розпізнаваних ними мов).

Детермінований скінченний автомат-розпізнавач. Детермінований скінченний автомат (ДКА) – це п’ятірка , де

X – скінченний алфавіт вхідних символів,

Y – скінченна множина станів,

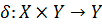– функція переходів,

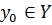– початковий (стартовий) стан,

– множина допускаючих станів.

Розширена функція переходів 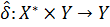, що співставляє новий стан поточному стану і ланцюгу символів, індуктивно визначається наступним чином:

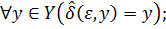
У такому випадку, якщо (стартуючи з початкового стану та обробивши ланцюжок 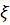, автомат опиняється в одному з допускаючих станів), кажуть, що він допускає цей ланцюжок. Множина допускаючих ланцюжків утворює мову L, яку розпізнає ДКА:

Клас мов, що розпізнає ДКА, називають регулярними мовами. Відомо, що він співпадає з класом мов, що описуються регулярними виразами й автоматними граматиками.

Детермінований скінченний автомат-перетворювач. Для того щоб наділити модель абстрактного скінченного автомата здатністю не тільки давати відповідь типу «так/ні», але й виконувати певні перетворення, в модель додають скінченний алфавіт вихідних символів 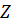і функцію виходу . Якщо функція виходу має вигляд , то обчислювач називається автоматом Мили, а якщо – автоматом Мура. Таким чином, розглядається шістка . Вона визначає автоматне відображення (перетворення, що виконується автоматом) так:

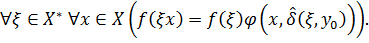
Автоматні відображення — це відображення «без передбачення»: переробляючи ланцюжок зліва направо, вони «не заглядають вперед». Наприклад, відображення, що співставляє ланцюжок йому самому, записаному в зворотному порядку, не являється автоматним.

Машина Тюрінга (МТ) – «найпотужніший» з абстрактних обчислювачів. Образно машину Тюрінга можна назвати «автоматом зі стрічковою пам’яттю». Більш формально МТ – це набір , где

W – скінченний алфавіт стрічкових символів,

Y – скінченна множина станів,

– функція переходів, яка по зчитаному зі стрічки символу і стану визначає новий стан, новий символ, що необхідно записати на стрічку, і напрям зсуву голівки (вліво, вправо або залишитись на місці),

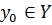– початковий стан,

b ∈ W – спеціальний стрічковий символ «пробіл»,

F ⊂ Y– множина допускаючих станів.

Відмітимо, що тільки нескінченна додаткова пам’ять (що може зберігати нескінченну кількість значень) збільшує обчислювальну потужність абстрактної машини. Прикладами є стек МП-автомата (автомата з магазинною пам’яттю) і стрічка машини Тюрінга, що пристосовуються для зберігання нескінченної кількості різних рядків ω ∈ W*. Якщо ж множина можливих значень пам’яті (позначимо її V) скінченна, то обчислювач завжди може бути перетворений в еквівалентний ДКА. Множина станів цього ДКА буде декартовим добутком Y×V множини станів вихідного обчислювача і множини значень його додаткової пам’яті.

Структурні моделі автоматів, що використовуються в задачах логічного керування, описуються зовсім в інших термінах. Автомат тут розглядається не як розпізнавач мови, а як пристрій керування. Тому в усіх структурних моделях крім множини вхідних дій X та множини станів Y існує й множина вихідних дій Z (всі три множини є скінченними).

За цією ознакою структурні автомати найбільше схожі на абстрактний скінченний автомат з виходом. Однак є і значні відмінності: ДКА з виходом розглядається як автоматне відображення вхідних рядків скінченної довжини у вихідні рядки тієї ж довжини. У випадку зі структурним автоматом кількість вхідних дій заздалегідь невідома й необов'язково скінченна. Вхідними впливами для системи управління можуть бути, наприклад, значення сигналізаторів. У відсутність непередбачених ситуацій робота такої системи ніколи не завершується. Тут значення має не весь нескінченний вихідний «рядок», а кожна вихідна дія окремо і саме в той момент часу (такт), коли вона згенерована. Іншими словами, моделі абстрактних автоматів застосовуються в трансформуючих системах (обчислюється функція над рядками), а структурні моделі - в реактивних системах (формують реакцію на вхідні дії від зовнішнього середовища).

У завданнях логічного керування значення має не тільки скінченність множин X, Y і Z, але й їх точна розмірність, оскільки вона впливає на складність реалізації пристрою керування. Крім того, елементи цих множин прийнято вважати бітовими векторами (іноді замість бітів зручніше використовувати, наприклад, цілі числа з невеликого діапазону). Теоретично це несуттєво, так як символи будь-якого скінченного алфавіту можна закодувати бітовими рядками однакової довжини. Такий вибір подання визначається швидше практичними міркуваннями: зручно вважати, що пристрій керування має декілька паралельних двійкових входів і виходів, причому кожен з них має певний сенс. Наприклад, на один з двійкових входів можуть подаватися різні значення в залежності від того, чи є поточна температура середовища допустимою, а на другий - в залежності від того, чи є допустимим тиск.

Для того щоб підкреслити векторну природу станів, вхідних і вихідних дій надалі будемо позначати їх як 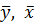и відповідно.

Автомати без пам’яті. Автомат, значення виходів z котрого залежать лише від значень входів x в даний момент часу і не залежать від передісторії, називається комбінаційним (однотактним), або автоматом без пам’яті. У цьому випадку термін «пам’ять» використовується в іншому смислі, ніж при опису абстрактних автоматів. Тут мова йде про основну пам’ять автомата: його керуючих станах, що накопичують інформацію про передісторію. У зв’язку з МП-автоматом і машиною Тюрінга говорилось про додаткову пам’ять: ту, що дана обчислювачу окрім його керуючих станів.

Строго кажучи, автомат без пам’яті не являється автоматом у смислі означення, де автоматом була названа скінченна динамічна система. Більш коректний термін для цього класу автоматів – комбінаційні схеми (КС). Стандартне позначення комбінаційної схеми приведено на рис. 5.

Функціонування комбінаційних схем описується співвідношенням:

) (x f z =.

Функция f у цьому соотношении обычно булева (ее аргументы и результат двоичны). Булевы функции принято задавать с помощью полностьюили не полностью определенных таблиц, которые в первом случае называются таблицами истинности, а во втором – таблицами решений. Более компактной формой представления булевых функций являются булевы формулы, которые всегда определяют функцию полностью.

Возвращаясь к терминам разд. 1.1, можно сказать, что комбинационная схема (в отличие от автоматов с памятью, рассматриваемых далее) является моделью сущности с простым поведением, поскольку ее выходное воздействие не зависит от состояния.

Автоматы с памятью. Автомат, значения выходов z которого зависят не только от значений входов x в данный момент времени, но и от предыстории, называется последовательностным(многотактным), или автоматом с памятью.

Автомат с памятью в отличие от комбинационной схемыявляется автоматом в обозначенном выше смысле – он представляет собой конечную динамическую систему. Отметим, что способ описания последовательностных автоматов, принятый в логическом управлении, отличается от уравнений динамических систем (формулы (1) и (2)). В логическом управлении время в явном виде не используется. Автоматы представляются в виде структурных схем, которые состоят из элементов двух типов: комбинационных схем и элементов задержки (ЭЗ). Для каждого элемента схемы отдельно записывается уравнение преобразования, которое он осуществляет (зависимость выходного сигнала от входного). Элементы задержки на самом деле не преобразуют сигнал: они передают на выход то же, что получили на вход, но через некоторый заданный промежуток времени (в данном случае, один такт), однако, в уравнениях эта задержка в явном виде не отражается.

Ниже рассмотрены наиболее важные классы последовательностных автоматов: автоматы без выходного преобразователя, автоматы Мура, Мили и смешанные автоматы.

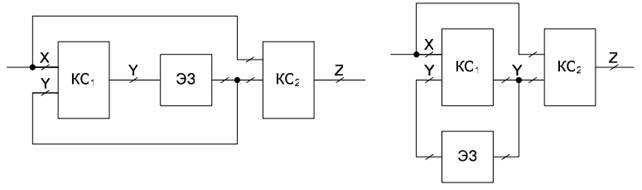
Автоматы без выходного преобразователя. Структурная схема автомата без выходного преобразователя первого рода приведена на рис. 6 (слева), а второго рода – на рис. 6 (справа). Здесь комбинационная схема реализует функцию переходов автомата, а элемент задержки и обратная связь, которая передает сигнал с выхода автомата обратно на вход, обеспечивают его память.

Рис. 6. Автоматы без выходного преобразователя: первого рода (слева) и второго рода (справа)

Элементы рассмотренных схем описываются следующими соотношениями (уравнения (3) и (4) описывают автоматы первого и второго рода соответственно):

y z

z x y

=

=), (δ

(3)

z y

y x z

=

=), (δ

(4)

Здесь функция δ, вычисляемая комбинационной схемой КС, имеет смисл функции переходов автомата.

Обратим внимание читателя на различие терминов «автомат без выхода» и «автомат без выходного преобразователя». Рассматриваемый структурный автомат формирует выходные воздействия. Отсутствие выходного преобразователя означает лишь то, что значения выходных переменных совпадают со значениями внутренних переменных автомата (на языке абстрактных автоматовэто значит, что функция выходов зависит только от состояний и является им тождественной). Иначе говоря, в этом случае каждое состояние автомата обозначается (кодируется) значением выходного воздействия в этом состоянии. Такое кодирование состояний называется принудительным.

Автоматы без выходного преобразователя имеют ограниченную область применения: они пригодны лишь тогда, когда число управляющих состояний автомата не превышает числа различных выходных воздействий. Приведем простой пример автоматизированного объекта управления, который не обладает таким свойством.

Рассмотрим счетный триггер, состоящий из кнопки, лампочки и управляющего автомата (рис. 1.11). Управляющий автомат в данном случае имеет одну двоичную входную переменную x, принимающую значение единица, если кнопка нажата,и ноль в противном случае, и одну двоичную выходную переменную z, устанавливаемую в единицу, если лампочку требуется включить, и в ноль – если выключить.

Рис. 1.11. Счетный триггер

Автомат Мура. Для преобразования свободно выбранных кодов состояний в значения выходных воздействий введем в автомат выходной преобразователь – еще одну комбинационную схему КС2, реализующую функцию выходов автомата (в отличие от первой комбинационной схемы КС1, реализующей функцию переходов).

Понятие структурного автомата Мура аналогично понятию абстрактного автомата Мура. В таком автомате выходное воздействие зависит только от состояния и не зависит от входного воздействия. Структурные схемы автоматов Мура первого и второго рода приведены на рис. 7. Автомат первого рода формирует выходные воздействия на основе текущих (не обновленных) значений внутренних переменных, а автомат второго рода, наоборот, сначала обновляет состояние, а затем использует его новое значение для вычисления выходного воздействия.

Автомат Мілі. По аналогии с абстрактными автоматами, структурный автомат, выходные воздействия которого зависят не только от состояния, но и от входных воздействий, называется автоматом Мили (рис. 8).

Дата добавления: 2014-01-07