Побудова аксонометричних зображень

За допомогою каркаса;

3. Кінематичний, тобто переміщенням ліній у просторі.

Складанням рівнянь поверхонь займається аналітична геометрія; вона розглядає криву поверхню як безліч точок, координати яких задовольняють деякому рівнянню. На рис. 4.3 приведений приклад поверхні, заданої аналітично (системою рівнянь алгебри).

Рис. 4.3

При каркасному способі задання крива поверхня задається сукупністю деякої кількості ліній, що належать поверхні. Лінії, що створюють каркас, як правило, беруть сімейство ліній, що виходять при перетині поверхні рядом паралельних площин. Цей спосіб застосовується при проектуванні кузовів автомобілів, в літако- і суднобудуванні, в топографії і т.п.

Нарисна геометрія вивчає кінематичні способи створення і задання кривих поверхонь. При цьому кожна крива поверхня розглядається як сукупність послідовних положень лінії твірної І, що переміщається в просторі за певним законом. Лінія твірної при своєму русі може залишатися незмінною, а може і змінювати свою форму. Такий спосіб утворення поверхні називається кінематичним, а сама поверхня – кінематичною.

Закон переміщення лінії твірної, як правило, задається за допомогою направляючих ліній та алгоритму переміщення створюваних напрямів. На кресленні кінематична крива поверхня задається за допомогою її визначника. Визначником поверхні називають сукупність умов, необхідних і достатніх для задання поверхні у просторі.

ЛЕКЦІЯ № · 5 КОМПЛЕКСНІ КРЕСЛЕННЯ ПОВЕРХОНЬ

5.1. Аксонометричні проекції.

5.2. Основна теорема аксонометрії (теорема Польке).

5.3. Стандартні аксонометричні проекції.

5.4. Коло в аксонометрії.

5.5. Побудова аксонометричних зображень.

5.1. Аксонометричні проекції

Аксонометричні зображення широко застосовуються завдяки добрій наочності та простоті побудов. Слово «аксонометрія» в перекладі з грецького означає вимірювання по осях. Аксонометричний метод може поєднуватися з паралельним і з центральним проектуванням за умови, що предмет проектується разом з координатною системою.

Суть методу паралельного аксонометричного проектування полягає в тому, що предмет відносять до деякої системи координат і потім проектують паралельними променями на площину разом з координатною системою.

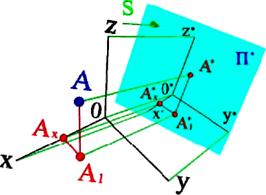
Рис. 5.1

На рис. 5.1 показана точка А, віднесена до системи прямокутних координат x,y,z. Вектор S визначає напрям проектування на площину проекцій П*.

Аксонометричну проекцію А₁* горизонтальної проекції точки А прийнято називати вторинною проекцією. Спотворення відрізків осей координат при їх проекціюванні на П' характеризується так званим коефіцієнтом спотворення.

Коефіцієнтом спотворення називається відношення довжини проекції відрізка осі на картині до його дійсної довжини. Так по осі x* коефіцієнт спотворення складає u=0*x*/0x, а по осі y* і z*, відповідно, υ=0*y*/0y і ω=0*z*/0z.

В залежності від відношення коефіцієнтів спотворення аксонометричні проекції можуть бути:

1. Ізометричними, якщо коефіцієнти спотворення на всіх трьох осях рівні між собою; в цьому випадку u=υ=ω.

2. Диметричними, якщо коефіцієнти спотворення на двох будь-яких осях рівні між собою, а на третій – відрізняється від перших двох.

3. Триметричними, якщо всі три коефіцієнти спотворення на осях різні.

Аксонометричні проекції розрізняються також і за тим кутом φ, який утворюється проектувальним променем з площиною проекцій. Якщо φ ≠ 90°, то аксонометрична проекція називається косокутною, а якщо φ = 90° – прямокутною.

5.2. Основна теорема аксонометрії (теорема ПОЛЬКЕ)

Розглянувши загальні відомості про аксонометричні проекції, можна зробити такі висновки:

· аксонометричні креслення оборотні;

· аксонометрична і вторинна проекції точки цілком визначають її положення в просторі.

Аксонометричні проекції оборотні, якщо відома аксонометрія трьох головних напрямів вимірювань фігури і коефіцієнти спотворення на цих напрямах. Аксонометричні проекції фігури є її проекціями на площині довільного положення при довільно вибраному напрямі проекціювання. Очевидно, можливо і зворотнє. На площині можна вибрати довільне положення осей з довільними аксонометричними масштабами.

У просторі завжди можливе таке положення натуральної системи прямокутних координат і такий розмір натурального масштабу по осях, паралельною проекцією яких є дана аксонометрична система.

Німецький вчений Карл Польке (1810 – 1876) сформулював основну теорему аксонометрії: три відрізки довільної довжини, що лежать в одній площині і виходять з однієї точки під довільними кутами, представляють паралельну проекцію трьох рівних і взаємно перпендикулярних відрізків, що виходять із однієї точки в просторі.

Згідно цієї теореми, будь-які три прямі в площині, що витікають з однієї точки і не співпадають між собою, можна прийняти за аксонометричні осі. Будь-які відрізки довільної довжини на цих прямих, відкладені від точки їх перетину, можна прийняти за аксонометричні масштаби. Ця система аксонометричних осей і масштабів є паралельною проекцією деякої прямокутної системи координатних осей і натуральних масштабів.

У практиці побудови аксонометричних зображень зазвичай застосовують лише деякі певні комбінації напрямів аксонометричних осей і аксонометричних масштабів: прямокутна ізометрія і диметрія, косокутна фронтальна диметрія, кабінетна проекція та ін.

5.3. Стандартні аксонометричні проекції

Згідно ДСТ 2.317-69, з прямокутних аксонометричних проекцій рекомендується застосовувати прямокутні ізометрію і диметрію. Між коефіцієнтами спотворення і кутом φ, створеним напрямом проекціювання і картинною площиною, існує така залежність:

u²+υ²+ω²=2+ctq²φ,

якщо φ=90⁰, то u²+υ²+ω²=2,

В ізометрії u=υ=ω і, отже, 3u²=2, звідки u=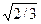≈ 0,82.

Таким чином, у прямокутній ізометрії розміри предмету за всіма трьома вимірюваннями скорочуються на 18%. ДСТ рекомендує ізометричну проекцію будувати без скорочення по осях координат (рис. 5.2), що відповідає збільшенню зображення проти оригіналу в 1,22 рази.

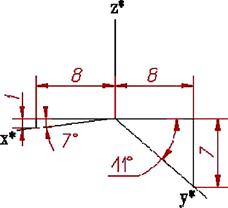
Рис. 5.2

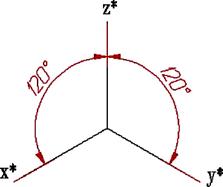
Рис. 5.3

При побудові прямокутної диметричної проекції скорочення довжин по осі у' (рис. 5.3) приймають удвічі більшим, ніж по двох інших, тобто вважають, що u=ω, а υ=0,5u. Тоді 2u²+(0,5u)²=2, звідки u²=8/9 і u ≈0,94, а υ=0,47. У практичних побудовах від таких дробних коефіцієнтів зазвичай відмовляються, вводячи масштаб збільшення, що визначений співвідношенням 1/0,94=1,06, і тоді коефіцієнти спотворення по осях x' і z' рівні одиниці, а по осі у' удвічі менші υ=0,5. З косокутних аксонометричних проекцій ДСТ- ом передбачено застосування фронтальної та горизонтальної ізометрії і фронтальної диметрії (останню ще називають кабінетною проекцією).

5.4. Коло в аксонометрії

При паралельному проекціюванні кола на будь-яку площину П* отримуємо її зображення в загальному випадку у вигляді еліпса (рис. 5.4).

t₂ // CB; t₄ // AD; t₆ // CB; t₈ // AD.

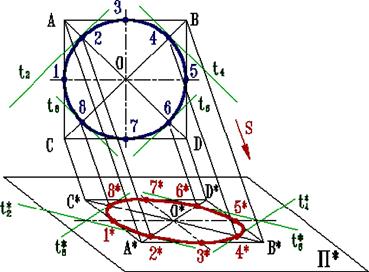
Рис. 5.4

Як би не була розташована площина кола, спочатку доцільно побудувати паралелограм A*B*C*D* – паралельну проекцію квадрата ABCD, описаного біля даного кола, а потім за допомогою восьми точок і восьми дотичних вписати в нього еліпс. Точки 1, 3, 5 і 7 – середини сторін паралелограма. Точки 2, 4, 6 і 8 розташовані на діагоналях так, що кожна з них ділить напівдіагональ у співвідношенні 3:7. Дійсно, на основі властивостей паралельного проекціювания можна записати, що А₂/1О=A*2*/2*O*, тобто А₁/1О·=·(r √2-r)/r ≈3/7.

З восьми дотичних до еліпса перші чотири – це сторони паралелограма, а решта t₂, t₄, t₆, t₈ – прямі, паралельні його діагоналям. Так дотична t₂* до еліпса паралельна діагоналі C*D*.

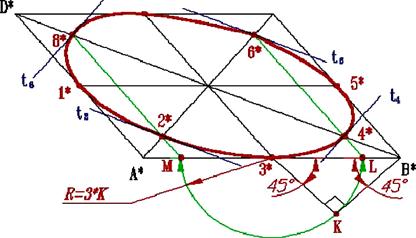
Рис. 5.5

Пояснюється це тим, що t₂* і C*D* є проекціями двох паралельних прямих t₂ і CD. Графічні побудови, що передують викреслюванню самого еліпса, доцільно виконувати в наступній послідовності (рис. 5.5):

1. Побудувати аксонометричну проекцію квадрата – паралелограм A*B*C*D* і провести діагоналі A*C* і B*D*;

2. Відзначити середини сторін паралелограма – точки 1*, 3*, 5* і 7*;

3. На відрізку 3*B*, як на гіпотенузі, побудувати прямокутний рівнобедрений трикутник 3*KB*;

4. З точки 3* радіусом 3*K описати півколо, яке перетне A*B* в точках L і M; ці точки ділять відрізок 3*A* і рівний йому відрізок 3*B* у відношенні 3:7;

5. Через точки L і М провести прямі, паралельні бічним сторонам паралелограма, і відзначити точки 2*, 4*, 6* і 8*, розташовані на діагоналях;

6. Побудувати дотичні до еліпса в знайдених точках. Дотичні t₂ і t₆ паралельні BD, а дотичні t₄ і t₈ паралельні AC.

7. Отримавши вісім точок і стільки ж дотичних, можна з достатньою точністю накреслити еліпс.

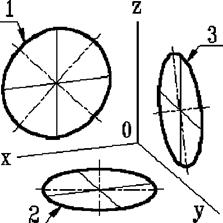
Рис.5.6

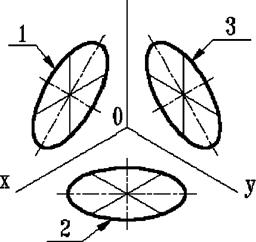
Рис. 5.7

ДСТ 2.317-69 визначає положення кіл, що лежать у площинах, паралельних площинам проекцій для прямокутної ізометричної проекції (рис. 5.6) і для прямокутної диметрії (рис. 5.7).

Якщо ізометричну проекцію виконують без спотворення по осях x, у, z, то велика вісь еліпсів 1,2,3 рівна 1,22, а мала вісь – 0.71 діаметра кола.

Якщо ізометричну проекцію виконують із спотворенням по осях x, у, z, то велика вісь еліпсів 1, 2, 3 рівна діаметру кола, а мала – 0.58 діаметра кола.

Якщо диметричну проекцію виконують без спотворення по осях x і z, то велика вісь еліпсів 1, 2, 3 дорівнює 1,06 діаметра кола, а мала вісь еліпса 1 – 0.95, еліпсів 2 і 3 – 0.35 діаметра кола.

Якщо диметричну проекцію виконують із спотворенням по осях х і z, то велика вісь еліпсів 1, 2, 3 дорівнює діаметру кола, а мала вісь еліпса 1 – 0.9, еліпсів 2 і 3 – 0,33 діаметра кола.

1 – еліпс (велика вісь розташована під кутом 90^О до осі у);

2 – еліпс (велика вісь розташована під кутом 90^О до осі z);

3 – еліпс (велика вісь розташована під кутом 90^О до осі х).

Перехід від ортогональних проекцій предмету до аксонометричного зображення рекомендується здійснювати в такій послідовності (рис. 5.8):

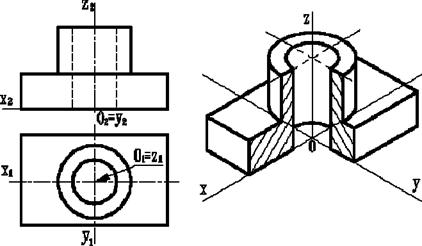
Рис. 5.8

1. На ортогональному кресленні розмічають осі прямокутної системи координат, до якої відносять даний предмет. Осі орієнтують так, щоб вони допускали зручне вимірювання координат точок предмету. Наприклад, при побудові аксонометрії тіла обертання одну з координатних осей доцільно сумістити з віссю тіла.

2. Будують аксонометричні осі з таким розрахунком, щоб забезпечити якнайкращу наочність зображення і видимість тих чи інших точок предмету.

3. На одній з ортогональних проекцій предмету креслять вторинну проекцію.

4. Створюють аксонометричне зображення, для наочності роблять виріз чверті.

ДСТ 2.317-69 визначає умовності та способи нанесення розмірів при побудові аксонометричного зображення. При цьому основну увагу слід звернути на таке:

· Лінії штрихування перетину в аксонометричних проекціях наносять паралельно одній з діагоналей проекцій квадратів, що лежать у відповідних координатних площинах, сторони яких паралельні аксонометричним осям, рис. 5.9.

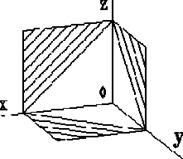
Рис. 5.9

· При нанесенні розмірів виносні лінії проводять паралельно аксонометричним осям, розмірні лінії – паралельно вимірюваному відрізку.

· В аксонометричних проекціях спиці маховиків і шківів, ребра жорсткості та подібні елементи штрихують.

5.5.1. Побудова аксонометричних проекцій плоских деталей

Побудова зображень плоских багатокутників зводиться до побудови аксонометричних проекцій їх вершин, які з'єднують між собою прямими лініями. У вигляді прикладу розглянемо побудову п'ятикутника, зображеного на рис. 5.10.

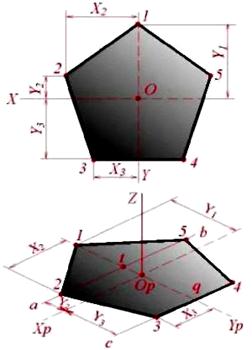
Рис. 5.10

Лінії X, Y приймемо за координатні осі. Проводимо ізометричні осі X_p та Y_p (рис. 5.10). Для побудови зображення точки 1 достатньо на осі Y_p відкласти відрізок O_p-1, рівний за величиною координаті Y₁. Потім відкладаємо в той же бік від точки O_p відрізок O_p-t, рівний координаті Y₂, і через точку t проводимо пряму ab, паралельну осі X_p. Координати X₂ вершин 2 і 5 п'ятикутника однакові за величиною, але різні за знаками; тому на ізометричному зображенні відкладаємо в обидва боки від точки t відрізки t-2= t -5 = X₂. Сторона 3-4 п'ятикутника паралельна осі X. Відклавши від точки q по осі Y_p відрізок q-O_p, рівний координаті Y₃, проводимо пряму cd, паралельну осі X_p, і відкладаємо на ній відрізки q -3 = q -4 = X₃. З'єднавши точки 1, 2, 3, 4, 5 прямими лініями, отримуємо аксонометричну проекцію п'ятикутника. Побудова аксонометричних проекцій плоскою кривою зводиться до побудови проекцій ряду її точок і з'єднання їх у певній послідовності. Hа рис. 5.11 показана побудова еліпса, розташованого в площині координатних осей X, Y.

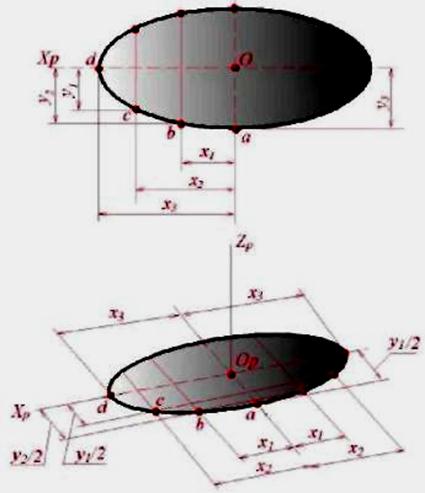
Рис. 5.11

Hа еліпсі намічаємо ряд точок і визначаємо їх прямокутні координати X та Y. Провівши аксонометричні осі, відкладаємо від точки O_p уздовж осі X_p відрізки, рівні за величиною координатам X намічених точок, а вздовж осі Y_p – відрізки, рівні за величиною половині координат Y (показана побудова точок а, b, c, d). Через кінці відрізків проводимо прямі, паралельні осям X_p, Y_p; на їх перетині отримуємо аксонометричні проекції відповідних точок, які з'єднуємо плавною лінією.

5.5.2. Побудова аксонометричних проекцій 3-вимірних об'єктів

Побудова проекцій многогранників зводиться до побудови їх вершин і ребер. Для призми зручніше починати з побудови вершин повністю видимої основи. Hа рис. 5.12 показана шестикутна призма, висота якої співпадає з віссю Z, а верхня основа розташована в площині осей X та Y. Ізометрична проекція цієї основи будується точно так, як і проекція п'ятикутника на рис. 5.10. Хід побудови зрозумілий з рис. 5.12. Оскільки довжина всіх бокових ребер призми рівна висоті призми h, то для побудови нижньої основи з вершин верхньої основи проведені прямі, паралельні осі Z_р, і на них відкладені відрізки, рівні h. Кінці відрізків з'єднані прямими лініями.

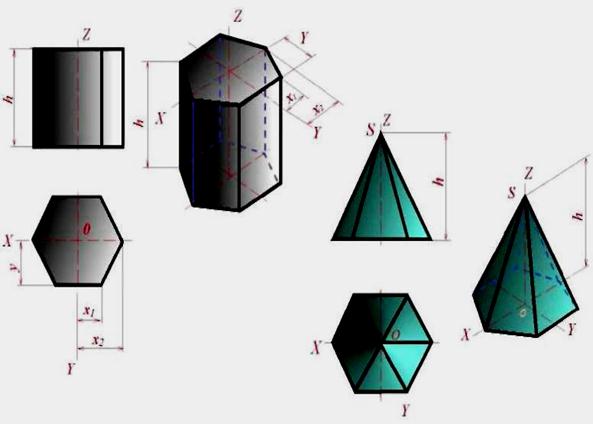
Рис. 5.12

Побудова аксонометричної проекції піраміди, зображеної на рис. 5.12, слід почати з побудови основи, а потім з точки О_р відкласти на осі Z_р висоту піраміди і отриману вершину піраміди S_р з'єднати з вершинами основи.

5.5.3. Побудова аксонометричних проекцій ліній перетину кривих поверхонь

Проекцію лінії перетину поверхонь можна будувати або за координатами ряду її точок, узятих з креслення проектованого предмету, або безпосередньо на аксонометричному зображенні, використовуючи для побудови допоміжні поверхні. Слід, по можливості, підбирати такі допоміжні поверхні, які із заданими поверхнями дають на кресленні прості для побудови лінії перетину.

Так, при побудові лінії перетину циліндрів допоміжні площини слід проводити паралельно прямолінійним створювальним циліндрових поверхонь. Hа рис. 5.13 площина R перетинає основи циліндрів по прямих Е_рF_р і О_рН_р, а циліндрові поверхні – по створювальних, що проходять через точки Е_р, F_р, Q_р, Н_р. Утворювальні, перетинаючись між собою, створюють точки (наприклад, точка А_р), приналежні лінії перетину.

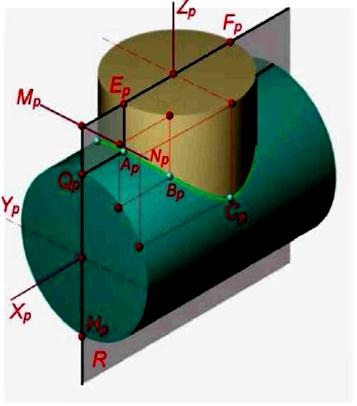
Рис. 5.13

Для побудови точок необхідної лінії зручно використовувати лінію перетину площин основ циліндрів (M_pN_p). Коли на кресленні відсутні проекції основ циліндрів, що перетинаються, то їх можна побудувати поза зображенням самої деталі (рис. 5.14).

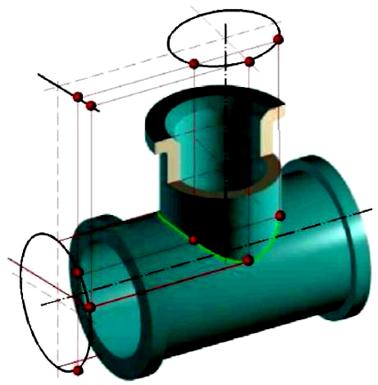
Рис. 5.14

ЛЕКЦІЯ №·6. БУДІВЕЛЬНЕ КРЕСЛЕННЯ

6.1. Загальні поняття.

6.2. Зміст, види і масштаби будівельних креслень.

6.3. Конструктивні елементи і схеми будівель.

6.4. Координаційні осі і модуль.

6.5. Розміри на будівельних кресленнях.

6.1. Загальні поняття

Будівельними кресленнями називають креслення, які містять проекційне зображення будівельних об'єктів або їх частин і інші дані, необхідні для їх зведення.

Будівельні об'єкти залежно від їх призначення підрозділяють на 4 основні групи:

· житлові та громадські будівлі – цивільні;

· промислові будівлі;

· сільськогосподарські будівлі;

· інженерні споруди – мости, тунелі, естакади і т.п.

Найбільш прогресивний метод будівництва – монтаж, тобто збірка будівлі або споруди з окремих елементів заводського виробника. Вони в готовому вигляді поступають на будівельний майданчик, при проектуванні за каталогами типових виробів підбирають необхідні елементи і деталі, а на кресленнях проставляють марки цих виробів.

За призначенням будівельні креслення ділять на дві основні групи:

· креслення будівельних виробів

· будівельно-монтажні креслення і схеми.

При виконанні та оформленні будівельних креслень необхідно керуватися ДСТ -ами, ЕСКД і СПДБ (системи проектної документації для будівництва).

6.2. Зміст, види та масштаби будівельних креслень

Масштаби креслень вибирають відповідно до ДСТ 2.302-68. Для житлових і громадських будівель:

1. Плани поверхів, підвалу, фундаментів, розрізи, фасади, монтажі, плани перекриттів – М1:100,1:200; 1:500.

2. Плани секцій, фрагменти планів, розрізів і фасадів – 1:50; 1:100.

3. Вироби і вузли – 1:5; 1:10; 1:20.

6.3. Конструктивні елементи та схеми будівель

Будівельні об'єкти складаються з окремих частин-конструкцій. Конструкції бувають збірні, що складаються з окремих елементів, та монолітні, такі, що виготовляються на місці монтажу (рис. 6.1).

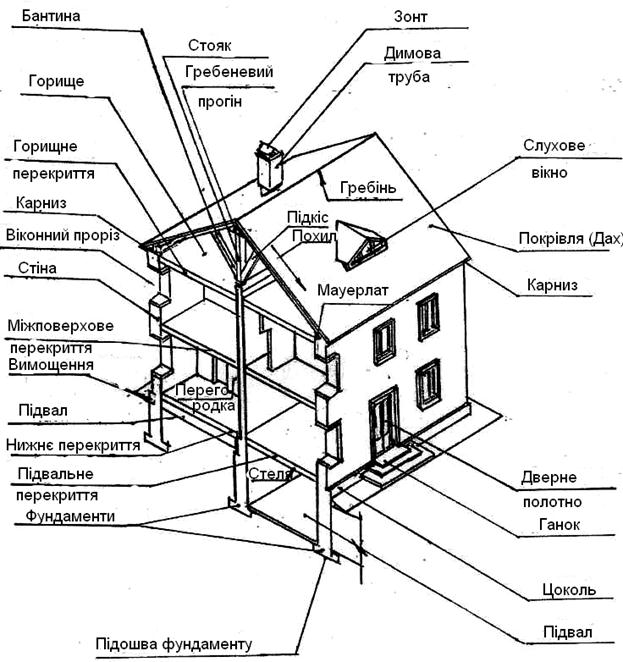
Рис. 6.1

6.4. Координаційні осі та модуль

1. Фундаментом під стіну або окрему опору (колону) називають підземельну частину будівлі, через яку передається навантаження на грунт. Фундаменти бувають стрічкові та стовпчасті.

2. Стіни в будівлі поділяються на зовнішні та внутрішні. Стіни бувають несучі (які передають навантаження на фундамент від власної ваги і ваги перекриття і даху), самонесучі (тільки від власної ваги) і навісні (навішуються на колони, складаються з окремих плит і навантаження від ваги передають на колони).

3. Перегородки – внутрішні захисні конструкції.

4. Цоколь – нижня частина зовнішньої схеми, що спирається на фундамент.

5. Перекриття – внутрішня горизонтальна конструкція, що розділяє будівлі на поверхи.

6. Покриття – верхня захищена конструкція, що визначає приміщення будівлі від зовнішнього середовища.

7. Крівля – верхній водоізолювальний шар покриття або даху будівлі.

8. Отвір – наскрізний отвір у стіні, призначений для установки вікна, дверей, воріт і ін.

9. Віконний блок – віконний перепліт з коробкою.

10. Сходова клітка – захищене капітальними стінами приміщення сходів.

11. Сходовий марш – нахилений елемент сходів із ступенями (не більше 18 ступенів).

12. Сходовий майданчик – горизонтальний елемент сходів між маршами. Основний (на рівнях поверхів) і проміжний (для переходу з одного маршу на інший).

Розрізняють дві основні конструктивні схеми будівлі:

· з несучими стінами (навантаження від перекриттів і даху, що сприймають стіни);

· каркасну (коли навантаження передається на систему зв'язаних між собою вертикально опор – колон і горизонтальних балок, на яких укладаються плити).

Основою для стандартизації та уніфікації в проектуванні, виготовленні виробів і будівництві служить Єдина модульна система (ЄМС), що є правилами координації розмірів на базі модуля. За величину основного модуля (М) прийнятий розмір 100·мм. На базі основного утворюються укрупнені та дробові модулі, які отримують множенням М на цілі та дробові числа: 6000, 3000, 1500 позначають 60М, 30М, 15М, (укрупнені модулі), а 50,20,10,5,2,1 – 1/2М, 1/5М, 1/10М, 1/20M, 1/50M, 1/100M (дроби).

Будівля або споруда в плані розчленовуються основними лініями на ряд елементів. Ці осі визначають розташування основних несучих конструкцій і називаються координаційними осями подовжніми і поперечними. Відстань між осями в плані називається кроком. Крок може бути подовжнім або поперечним (проліт – це відстань між осями в напрямі, який відповідає прольоту основної несучої конструкції перекриттю або покриттю. За висоту поверху Н_пов приймають відстань від рівня підлоги даного поверху до рівня підлоги вище розміщеного. В одноповерхових промислових будівлях висота поверху рівна відстані від рівня підлоги до нижньої грані конструкції покриття. Розміри кроків, прольотів і висот поверхів повинні прийматися рівними укрупненому модулю. Розміри конструктивних елементів повинні бути кратними основному модулю.

Координаційні осі наносять штрих-пунктирними лініями і позначають марками в колах радіусом в 12·мм. Для маркування застосовують арабські цифри і прописні букви. Розмір шрифту на один-два номери більший розміру шрифту чисел. Цифрами маркірують осі зі сторони будівлі з великою кількістю осей. Послідовність маркування – зліва направо, знизу догори. Зазвичай розташовують нижньою та лівою сторонами плану.

Прив'язка. У будівлях з несучими подовжніми і поперечними стінами прив'язку до координаційних осей зовнішніх і внутрішніх стін проводять таким чином: внутрішню грань зовнішньої стіни розміщують від координаційної осі на відстані М або 2М, тобто 100 або 200·мм (називається модульна прив'язка).

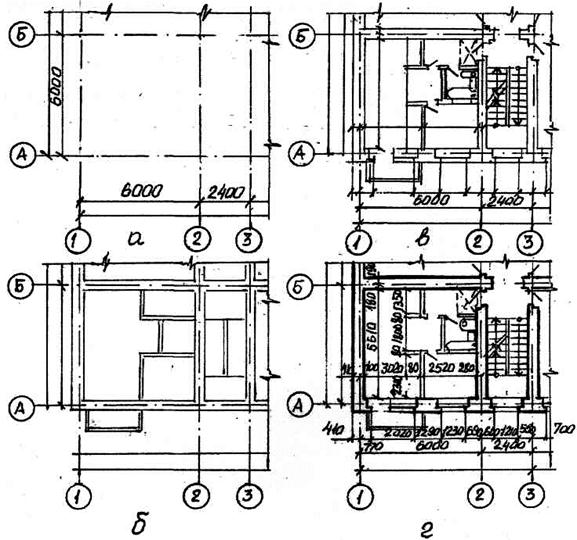
Рис. 6.2

Можлива також назва нульова прив'язка, коли координаційна вісь співпадає з внутрішньою поверхнею стіни (рис. 6.2, рис. 6.3). У внутрішніх стінах координаційна вісь повинна співпадати з віссю симетрії стіни, окрім стін сходових кліток і стін з каналами (центральними).

6.5. Розміри на будівельних кресленнях

Розміри на будівельних кресленнях проставляються в мм без позначення одиниці вимірювання. Наносять у вигляді замкнутого ланцюга (рис. 6.2). Розміри допускається повторювати. Замість стрілок застосовують зарубки у вигляді короткої суцільної основної лінії завдовжки 2…4·мм під 45^О до розмірної лінії. При цьому розміри лінії повинні виступати за крайні виносні на 1,3·мм (рис. 6.3).

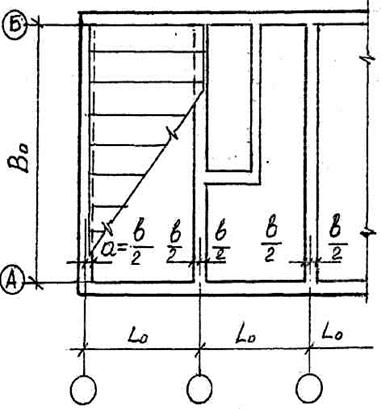
Рис. 6.3

Нанесення розмірів на плані будівлі виконують за ДСТ 2.307-68, що здійснюється таким чином. Поза габаритами плану поверху проставляють три ланцюжки розмірів:

1-й ланцюжок: прив'язка простінків і зовнішніх граней стін до координаційних осей, розміри простінків і отворів.

2-й ланцюжок: відстань між всіма координаційними осями, прив'язка осей крайніх колон.

3-й ланцюжок: габаритні розміри будівлі, тобто відстань між крайніми координаційними осями.

При нанесенні розмірів діаметрів, радіусів і кутів замість зарубок ставлять стрілки.

Відмітки рівнів (висоти, глибини) елементу будівлі або конструкції від будь-якого відлікового рівня, що приймається за нульовий, поміщають на виносних лініях (або лініях контуру). Їх позначають знаком "виносна лінія рівня відповідає поверхні". Відмітки вказують в метрах з трьома десятковими знаками. Умовну нульову відмітку позначають 0.000. Відмітки нижче умовної нульової позначають із знаком мінус, відмітки вище нульової – без знаку. На планах, якщо це необхідно, відмітки вказують із знаком +. Як нульовий для будівель зазвичай приймають рівень підлоги 1-го поверху. Відмітки при необхідності супроводжують пояснювальними написами: – Рівень підлоги; Рівень землі (рис. 6.4).

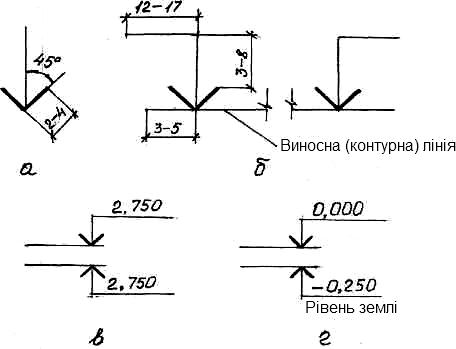
Рис. 6.4

На планах напрям ухилу площини вказують стрілкою, над якою (якщо потрібно) проставляють величину ухилу.
ЛЕКЦІЯ № · 7 Архітектурно–будівельне креслення

7.1. Склад робочих креслень.

7.2. Викреслювання плану будівлі.

Дата добавления: 2014-01-07