Контрольні питання. 1. Коли застосовують відхилення якості готового продукту як критерій ке-рування АПД ?

1. Коли застосовують відхилення якості готового продукту як критерій ке-рування АПД? Як в цьому випадку формують мету керування з допомогою те-хнологічної складової прибутку?

2. Коли застосовують продуктивність АПД як критерій керування цим апа-ратом? Як в цьому випадку формують мету керування з допомогою техноло-гічної складової прибутку?

3. Коли застосовують питомий вихід продукту як критерій керування АПД? Як в цьому випадку формують мету керування з допомогою технологічної скла-дової прибутку?

4. Наведіть постановку задачі динамічної оптимізації періодичних техноло-гічних процесів. Для чого у розв’язанні цієї задачі використовують математич-ні прогнозні моделі?

5. Наведіть постановку задачі динамічної оптимізації періодичних техно-логічних процесів. Для чого у разі розв’язання цієї задачі використовують фі-зичні прогнозні моделі?

6. Чому зміна тривалості циклу роботи (ТЦР) АПД впливає на його продук-тивність? Як ставиться та розв’язується задача вибору ТЦР з допомогою гра-фічного методу?

7. Чому зміна тривалості циклу роботи (ТЦР) АПД впливає на його продук-тивність? Як ставиться та розв’язується задача вибору ТЦР з допомогою аналі-тичного методу?

8. Чому зміна тривалості циклу роботи (ТЦР) АПД впливає на його продук-тивність? Як станоться та розв’язується задача ТЦР з допомогою розрахунково-графічного методу?

9. Як використовують одновимірний пошук з допомогою локалізації екстре-муму у разі застосування розрахунково-графічного методу вибору тривалості циклу роботи АПД?

10. Як використовують одновимірний пошук з допомогою золотого перерізу у разі застосування розрахунково-графічного метода вибору тривалості циклу роботи АПД?

Тема 6. РЕАЛІЗАЦІЯ РЕГУЛЯТОРІВ В МІКРОПРОЦЕСОРНИХ СИСТЕМ АВТОМАТИЗАЦІЇ (МСА)

Застосування прямого та непрямого керування при використанні ЕОМ. Позиційні та швидкісні регулятори. Реалізація керувальних функцій в регулюва-льних та логічних контролерах. Стандартні алгоритми регулювання, їх передатні функції та параметри настроювання. Використання автопідстро-ювання. Нелінійні логічні регулятори та види логічних функціональних при-строїв. Інтелектуальні регулятори нового покаління: експертні, асоциативні, нечіткі та нейромережні регулятори

1. Загальні положення. Існують два режими реалізації керуючих функцій в МСА: супервізорне (непряме) і безпосередне (пряме) керування. При супер-візорному керуванні ЕОМ змінює завдання х*(t) або (та) вектор параметрів на-строювання локального регулятора k (t). При прямому керуванні ЕОМ безпосередньо керує виконавчим механізмом (ВМ), змінюючи сигнал u(t). Як відомо, в сучасних системах керування функції локальних регуляторів вико-нують МПК, а функції ЕОМ – персональні комп’ютери (ПК), тому структура цих двох варіантів реалізації керуючих дій має вигляд, наведений на рис.15.

При цьому ліва частина малюнка відповідає супервізорному керуванню, права частина – контролерному керуванню без вживання терміна безпосереднє (пряме) керування, тому що в обох випадках функції регулятора і станції керування виконує МПК.

2. Позиційні та швидкісні алгоритми регулювання. Головна особ-ливість цих алгоритмів полягає у квантуванні за часом вихідного керуючого си-гналу, тому рівняння такого (іноді його називають цифровим) ПІ-регулятора має такий вигляд:

u_k = k_p Dx_k + u_ò.k, u_ò.k = u_ò.k-1+ (k_pT₀ /T_и ) Dx_k, (27)

де u_k – клерувальна дія на k-му кроці; Dx_k – розузгодження на k-му кроці; T₀ – період розрахунку u_k, який може співпадати з періодом опитування датчиків або бути більшим цього періоду; u_ò.0=0. Рівняння (27), як і всі операції з інтегрування в ЕОМ, щоб не використовувати багато пам’яті, побудовано з допомогою рекурентного співвідношення, коли замість запам’ятовування всіх значень розузгодження запам’ятовується тільки підсумок попереднього кроку.

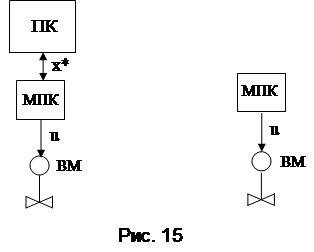Алгоритм (27) називають позиційним, оскільки при його використанні на виході ЕОМ формується повне значення u, а значить при відмові ЕОМ u =0 і в залежності від конструктивних особливостей ВМ він може займати крайнє положення, що є суттєвим недоліком цих алгоритмів. Цього недоліку не мають швидкісні алгоритми, які використовують в тих випадках, коли інтегрування відбувається не в обчислювальному пристрої, а в ЦАП або в ВМ (наприклад, крокові електродвигуни, електродвигуни ВМ постійної швидкості). У цьому випадку на виході ЕОМ формується не u, а D u:

Du = Du_к – Du_к-1 = k_p(Dx_к – Dx_к-1)+(k_pT₀Dx_к/T_и). (28)

Розглянуті алгоритми регулювання дозволяють доволі просто реалізувати комбіновані, автономні та інші багато контурні системи. В цьому випадку алго-ритми (27) і (28) зміняться таким чином:

u_k = k_p Dx_k + u_ò.k + u_k.k, (29)

Du = k_p(Dx_к – Dx_к-1) + (k_pT₀ Dx_к / T_и) + Du_k.k (30)

де u_k.k – сигнал компенсатора; Du_k.k – приріст сигналу компенсатора. При реа-лізації (29) і (30) з допомогою МПК треба пам’ятати, що крім обмеження на u і Du, яке існує в стандартних алгоритмах регулювання, необхідно також обме-ження сигналів на u і Du, які формуються як сума сигналів регулятора та ком-пенсатора.

3. Реалізація керуючих функцій з допомогою контролера. Для цього ви-коритовуються стандартні алгоритми, які є бібліотеках мікропроцесорних контролерів (МПК). У всіх бібліотеках МПК містяться алгоритми регуляторів з аналоговим і імпульсним виходом. Перші призначені для управління пнев-матичними виконавчими механізмами (ВМ) і іншими регуляторами в каскад-них системах, другі застосовують для управління електродвигунними ВМ пос-тійної швидкості. Дамо коротку характеристику бібліотекам різних контролерів з точки зору наявності в них алгоритмів регулювання.

Реміконти великої і середньої канальності (РВСК). Ці контролери мають найбільш розвинуту бібліотеку алгоритмів регулювання: 7 алгоритмів аналого-вого регулювання і 9 алгоритмів імпульсного регулювання.

Базовий (стандартний) алгоритм РАС для аналогового ПІД-регулювання (код 01) здійснює перетворення сигналу у відповідності до передатною функцією:

W(p) = k_п+ k_п(1/T_и p) + {k_пT_д p/ [(T_д p/8) + 1] [(T_д p/4) + 1]}, (31)

де k_п – коефіцієнт пропорціональності, який змінюється в інтервалі –127,8... +127,8 абсолютних одиниць з мінімальним кроком 0,1; T_и – час ізодрома який змінюється в інтервалі 0,01...136 хв при T_и = 0,27 с; T_д – час диференцювання, який змінюється в інтервалі 0,01...272 с при T_и = 0,51 с. Мінімальний крок зміни обох часових параметрів близько 3%.

Функціонально алгоритм РАС має два вхідних суматора, в яких підсумо-вується і масштабується п’ять вхідних змінних; інерційний фільтр для суматора перших трьох змінних; суматор, що формує розузгодження; вузол статичного розбалансування; зону нечутливості; інвертор; ПІД-ланку; пороговий елемент; нуль-орган, який контролює розузгодження і з’єднаний з дискретними вихо-дами алгоритму; вузол дистанційного керування (входи 6,7,8) з ланкою дина-мічного балансування.

Базовий (стандартний) алгоритм РІС для імпульсного ПІД-регулювання (код 11) здійснює перетворення сигналу у відповідності до передатної функ-цією (31), але з загальним коефіцієнтом T_м /T_м.о, де T_м і T_м.о – відповідно розра-хований повний час переміщення ВМ та його дійсне значення. Алгоритм міс-тить ПІД²-ланку, яка разом з ВМ реалізує ПІД-закон регулювання.

Автопідстроювання має ціла група алгоритмів РВСК, які використовую-ться на об’єктах з нестаціонарними параметрами. Це алгоритми РАП (04), ПАП (08), РИП (14), РПП (15), ПИП (18), ППП (19). У цих алгоритмів за винятком РПП і ППП входи 4 і 5 використовуються для змінювання коефіцієнтів пропорційності (вхід 4) та T_и і T_д (вхід 5) за формулою:

К = К₀ [1 + (К4(5) Х4(5)/13)], (32)

де К₀ – початкове значення k_п,T_и,T_д; Х4(5) - сигнали автопідстроювання; К4(5) – масштабні коефіцієнти, що визначають ступінь впливу сигналів Х4(5) на параметри k_п,T_и,T_д. Алгоритми РПП та ППП мають повне автопідстроювання, використовуючи для цього крім входів 4 і 5 ще вхід 2 підстроювання сталої ча-су ВМ T_м, а вхід 3 – для підстроювання зони нечутливості D за формулою (32).

Ломіконти. Їх бібліотека м ає 4 стандартних алгоритмидля регулювання: ПІД-А (аналоговий), ПІД-І (імпульсний), ПІ-А, ПІ-І, які фактично реалізують частину функцій алгоритмів РАС, РІС, ПАС і ПСІ РВСК, починаючи з су-матора перед елементом, що формує зону нечутливості, і закінчуючи обмежу-вачем на виході алгоритму. Передатні функції ПІД-А і ПІД-І алгоритмів пов-торюють передатні функції РАС і РІС алгоритмів, але без [(T_дp/4)+1] у знаме-ннику Д-складової. Авто підстроювання параметрів здійснюється за формулою:

К = К_о[1 + (К_ап Х_ап/512)],

де К_ап – коефіцієнт автопідстроювання; Х_ап – вхід автопідстроювання. У вказаних алгоритмах стала часу може змінюватися в діапазоні 1 с... 72 год 14 хв 56 с, коефіцієнт пропорціональності – 0... 100, масштабний коефіцієнт – 0... 1,99.

Реміконти малої канальності (РМК). Їх бібліотека м ає 2 стандартних алгоритмудля регулювання: РАН (аналоговий) і РІМ (імпульсний). Їх відмі-нність від алгоритмів РАС і РІС полягає у такому:

· підсумовуються тільки дві вхідні змінні, одна з яких масштабується і фі-льтрується;

· алгоритм має режим настроювання, в якому автоматично визначаються оптимальні параметри настроювання.

Передатна функція алгоритму РАН має такий вигляд:

W(p) = k_п+ k_п(1/T_и p) + {k_пT_д p/ [(T_д p/8) + 1] ²},

де k_п змінюється у тому ж діапазоні, що і у РАС-алгоритму; T_и і T_д можуть змінюватися, як і решта сталих часу у діапазоні 0... 819 с, хв, год (в залежності від настроювання); T_д = k_дT_и (при k_дT_и > 819, значення T_д дорівнює не скін-ченості); масштабний коефіцієнт змінюється в діапазоні –15,99... +15,99. Ана-логічно формується і РІМ-алгоритм, передатна функція якого відрізняється від передатної функції РАН-алгоритму множником T_м /T_м.о.

Підсумовуючи розглянуте, зазначимо що найбільшу ступінь інтеграції фу-нкцій автоматичного регулювання мають стандартні алгоритми РВСК. При використанні стандартних алгоритмів РМК вони повинні бути доповнені алго-ритмом ручного управління, алгоритмом оперативного регулювання і в необ-хідних випадках (при кількості входів більш одного) – алгоритмом підсумо-вування. При використанні стандартних алгоритмів ломіконта до вказаних до-даткових алгоритмів необхідно додати також алгоритм фільтрації.

4. Нелінійні логічні регулятори (НЛР). НЛР відносяться до нестандарт-них алгоритмів регулювання, в яких регулювальна дія на об’єкт є нелінійною функцією розузгодження, причому можуть бути як статичні, так і динамічні нелінійності. В НЛР нелінійний закон регулювання реалізується з допомогою логічних функцій. Застосування НЛР є ефективним алгоритмічним способом покращення якості функціонування АСР на об’єктах з несприятливими дина-мічними властивостями. Цей спосіб має суттєві переваги перед інформаційними способами, що домінують в апаратних системах автоматизації і пов’язані з застосуванням багато контурних АСР. По-перше, алгоритмічний спосіб більш економічний у зв’язку з тим, що не потребує додаткових інформаційних кана-лів. По-друге, він доволі просто, реалізується програмним шляхом в МСА.

Загальний вигляд структурної схеми АСР з НЛР наведений на рис.16.

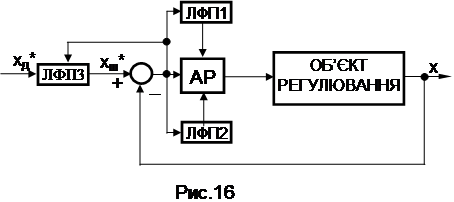В такій системі використовуються один або кілька логіко-функціональних пристроїв (ЛФП), які в залежності від розузгодження Dx або його похідної вми-кають чи вимикають складові закону регулювання (ЛФП1), змінюють пара-метри настроювання регулятора (ЛФП2) або формують штучне завдання x_ш* на деяких ділянках перехідного процесу (ЛФП3).

Прикладом найпростішого НЛР з ЛФП1 є ПІНД-регулятор, в якому в зале-жноті від значення розузгодження Dx вмикається або вимикається І-складова:

u = k_p{ Dx + (e ò Dx dt / T_и ) + [T_д d(Dx)/dt]}, (33)

де e – логічна функція розузгодження: e = 1, коли |Dx| < d, та e = 0, коли |Dx| >> d, причому значення d залежить від припустимої статичної похибки системи.

Прикладом НЛР з ЛФП2 є ПІД-регулятор з подвійною П-складовою – П2ІД:

u=k_p{ Dx |Dx| + (òDxdt / T_и ) + [T_д d(Dx)/dt]}. (34)

Для зменшення впливу Д-складової на перехідний процес вона може розрахо-вуватися не за значенням розузгодження Dx, а безпосередньо за значенням регульованої величини x.

І накінець, прикладом НЛР з ЛФП3 є регулятор зі зміною завдання за та-ким алгоритмом:

x_ш* = x_д*, коли d(Dx)/dt > 0; x_ш* = x, коли d(Dx)/dt = 0;

x_ш* = x_me^-lt, коли d(Dx)/dt < 0; (35)

де x_ш*,x_д*– відповідно штучне і дійсне значення завдання; x_m – значення змі-нної в момент відсічки дійсного завдання, тобто при d(Dx)/dt=0; l – параметр затухання експоненти. При використанні НЛР необхідно вирішити дві задачі: розробити програмно-конфігураційну схему реалізації такого регулятора та ви-значити його оптимальні параметри настроювання.

5. Інтелектуальні регулятори нового покоління. Розглянуті вище НЛР іноді відносять до інтелектуальних регуляторів 1-го покоління, враховуючи що вони змі-нюють режими роботи в залежності від ситуації на об’єкті. Нове, 2-го покоління інтелектуальних регуляторів пов’язано зі створенням регуляторів з розвинутою пам’яттю, наявністю стадії навчання в їх життєвому циклі та мож-ливістю застосування їх у разі невизначеності характеристик об’єкта регулю-вання. До них відносяться експертні, асоціативні, нечіткі та нейромережні регулятори.

Експертний регулятор (ЕР) призначений для активної самодіагностики об’єкта регулювання (ОР) з допомогою аналізу змін параметрів ОР та їх ком-пенсації перенастроюванням ЕР, структура якого складається з таких компо-нентів:

база знань містить теоретичні емпіричні знання з предметної області теорії автоматичного керування і ОР, включаючи знаннями, отримані під час навча-ння з допомогою аналізу динамічних властивостей системи, а також знання про діапазони зміни керуючих дій і збурень, порядок математичної моделі. При цьому сукупність сформованих теоретичних і емпіричних знань представляють вигляді продукційних правил, що регламентують автономне функціонування ЕР на кожному етапі його роботи;

база алгоритмів (іноді може входити в склад бази знань) має закони регу-лювання, алгоритми параметричної ідентифікації і синтезу АСР;

база даних зберігає поточні значення змінних ОР і характеристики про-цесів регулювання;

механізм логічного виводу формує експертні висновки, на базі яких відбу-вається перенастроювання ЕР.

Регулятор з асоціативною пам’яттю на базі інформації про стан об’єк-та регулювання миттєво вибирає із асоціативної пам’яті значення керуючої дії або параметрів настроювання регулятора. Навчання цього регулятора пов’язане з накопичення елементів асоціативної пам’яті, в якій певним значенням змінних x, z, Dх та швидкостям їх зміни відповідають певні значення u та параметрів настроювання регулятора. Найчастіше така система є системою з дискретно змінюваними параметрами.

Нечіткий регулятор побудований з використанням нечіткої (розмитої) логіки або «Fuzzy-Logic» (фуці-логіки), причому знання про взаємодію з об’єк-том регулювання представляються у вигляді правил ЯКЩО (ситуація на об’єк-ті) – ТО (реакція) або ЯКЩО – І (додаткова інформація про об’єкт) – ТО. Нап-риклад, ЯКЩО (тиск пари великий) І (температура збільшується), ТО (вентіль подачі палива закрити). Структурно регулятор складається з таких компонентів:

блок фуціфікації переводить значення змінних у лінгвістичні величини. Для цього їх числові значення характеризують лінгвістичними величинами (ЛВ) «мало», «середньо», «багато». Кожна ЛВ описується фуці-правилами (ФП), причому вони можуть накладатися одне на інше і одній змінній декілька ФП можуть давати різні значення;

база правил зберігає фуці-правила для кожної ЛВ;

блок формування логічного рішення використовує правила типу ЯКЩО-ТО і ЯКЩО-І-ТО, які в даному випадку описують поведінку регулятора. Цим пра-вилом досягається результат, при якому для будь-якої ЛВ керуючої дії як мі-німум одне правило буває дійсним;

блок дефуціфікації генерує керуючу дію, яку на виході регулятора отри-мують як нечітку множину у формі ФП. Найбільш часто в цьому випадку ви-користовується метод центру тяжіння, при якому керуюча дія обчислюється як значення абсциси центру тяжіння площини, що обмежена ФП та віссю абсциси.

Нейромережний регулятор (НМР) найчастіше створюється на базі бага-тошарової нейронної мережі (НМ) прямого розповсюдження, структура якої є дискетною решіткою з заданою кількістю прошарків та нейронів у прошарку, тому її функціонування описується рівнянням

N_k-1

А_kn = f _kn (S W_kin А_(k-1)i), n = 1,..., N_k ,

n=1

де N_k – кількість нейронів в k-му прошарку; А_kn – вихід n-го нейрона k-му про-шарку; W_kin – «вага» зв’язку від виходу n-го нейрона в (k–1)-му прошарку до входу n-го нейрона в k-му прошарку; f_kn(×) – функція перетворення n-го ней-рона в k-му прошарку, k=1,...,M (M – кількість прошарків в мережі).

Проектування НМР пов’язане з визначенням його розмірності (кількість прошарків і кількість нейронів в прошарку), а настроювання – з визначенням коефіцієнтів зв’язку. Коефіцієнти НМ можуть визначатися методом навчання або самоорганізації. Для настроювання коефіцієнтів методом навчання викори-стовують підключення промислового регулятора (ПР) та спеціальну вбудовану процедуру оптимізації. В самоорганізаційних НМ коефіцієнти зв’язку формую-ться в результаті нелінійних процесів конкурентної взаємодії між нейронами і механізмів саморегуляції.

Якщо динамічні процеси в нейронній мережі мало інерційні, то процеси оптимального настроювання параметрів мережі із-за інтегрального характеру процедур мають повільну збіжність. Це треба враховувати при застосуванні нейронних мереж в адаптивних систем керування, по-перше, під час узгоджу-ння швидкості пере-настроювання параметрів мережі, по-друге, при початково-му запусканні адаптивної системи. В останньому випадку із-за апріорної невизначеності в системі можуть виникати «пошукові блукання» і, як наслідок, великі перерегулювання. Для подолання цього недоліку використовують схему, коли попереднє НМР «навчають» з допомогою промислового регулятора (рис.17).

НМР формує керуючу дію u з допомогою послідовності попередніх зна-чень сигналу похибки керування Dх і даних прогнозу y нейромережного іденти-фікатора НМІ. Останній з допомогою сигналів u та x формує сигнал х_ін, який порівнюється з виходом об’єкту х і визначає таким чином похибку іденти-фікації Dх_ін. Оптимізатори регулятора ОР та ідентифікатора ОІ, використовую-чи похибки регулювання Dх і ідентифікації Dх_ін, визначають нові значення ве-кторних коефіцієнтів зв’язку W_р і W_ін, формуючи таким чином структуру НМР та модель об’єкта керування. НМР підіключено паралельно промисловому ре-гулятору ПР, який керує об’єктом. Cигнал розузгодження Du_нр використову-ється оптимізатором ОР для настроювання коефіцієнтов зв’язку НМР W_p. Од-ночасно відбувається настроювання параметрів моделі об’єкта в НМІ W_ін. Після закінчення попереднього навчання на вхід об’єкта замість ПР підмикається НМР.

Література для самостійної роботи: [5] С.24-26; [14 – 16].

Дата добавления: 2014-01-07