Втрати напору при ламінарній течії рідини

Як показують дослідження, при ламінарній течії рідини в круглій трубі максимальна швидкість перебуває на осі труби. У стінок труби швидкість дорівнює нулю, тому що частки рідини покривають внутрішню поверхню трубопроводу тонким нерухливим прошарком. Від стінок труби до її осі швидкості наростають плавно. Графік розподілу швидкостей по поперечному перерізу потоку являє собою параболоїд обертання, а переріз параболоїда осьовою площиною - квадратичну параболу (мал.4.3).

Рівняння, що зв'язує змінні υ і r, має такий вигляд:

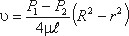
де P1 і P2 - тиску відповідно в перерізах 1 і 2.

Мал. 4.3. Схема для розгляду ламінарного потоку

У стінок труби величина r = R, означає швидкість υ = 0, а при r = 0 (на осі потоку) швидкість буде максимальною

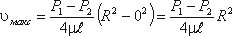
Тепер визначимо витрати рідини при ламінарній течії в круглій трубі. Тому що епюра розподілу швидкостей у круглій трубі має вигляд параболоїда обертання з максимальним значенням швидкості в центрі труби, то витрата рідини чисельно дорівнює об’єму цього параболоїда. Визначимо цей об’єм.

Максимальна швидкість дає висоту параболоїда

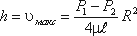
Як відомо з геометрії, об’єм параболоїда висотою h і площею ρR² дорівнює

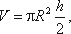
а в нашому випадку

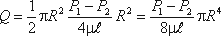
Якщо замість R підставити діаметр труби d, то формула (4.4) отримає вигляд

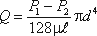
Витрати в трубі можна виразити через середню швидкість:

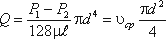
звідки

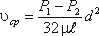
Для визначення втрат напору при ламінарній течії рідини в круглій трубі розглянемо ділянку труби довжиною l, по якій потік тече в умовах ламінарного режиму (мал.4.3).

Втрата тиску в трубопроводі буде рівна

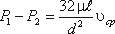
Якщо у формулі динамічний коефіцієнт в'язкості µ замінити через кінематичний коефіцієнт в'язкості υ і щільність ρ і розділити обидві частини рівності на об'ємну вагу рідини γ = γ g, то отримаємо:

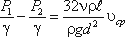
Так як ліва частина отриманої рівності дорівнює втратам напору h_пот у трубі постійного діаметра, то остаточно ця рівність прийме вигляд:

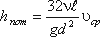
Рівняння може бути перетворене в універсальну формулу Вейсбаха-Дарсі, яка остаточно записується так:

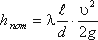
де λ - коефіцієнт гідравлічного тертя, який для ламінарного потоку обчислюється по вираженню:

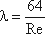
Однак при ламінарному режимі для визначення коефіцієнта гідравлічного тертя λ Т.М. Башта рекомендує при Re < 2300 застосовувати формулу

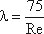
Дата добавления: 2014-01-07