Витікання через малі отвори в тонкій стінці при постійному напорі

Лекція 5. ВИТІКАННЯ РІДИНИ З ОТВОРІВ, НАСАДОК І З-ПІД ЗАТВОРІВ

Розглянемо різні випадки витікання рідини з резервуарів, баків, казанів через отвори й насадки (короткі трубки різної форми) в атмосферу або простір, заповнене газом або тією ж рідина. У процесі такого витікання запас потенційної енергії, який має рідина, що перебуває в резервуарі, перетворюється в кінетичну енергію вільного струменя.

Основним питанням, яке цікавить у цьому випадку, є визначення швидкості витікання й витрати рідини для різних форм отворів і насадок.

Розглянемо великий резервуар з рідиною під тиском Р₀, що має малий круглий отвір у стінці на досить великій глибині Н₀ від вільної поверхні (мал.5.1).

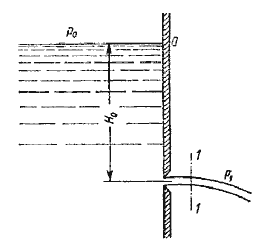
Мал. 5.1. Витікання з резервуара через малий отвір

Рідина випливає в повітряний простір з тиском Р₁. Нехай отвір має форму, показану на мал.5.2, а, тобто виконане у вигляді свердління в тонкій стінці без обробки вхідної кромки або має форму, показану на мал.5.2, б, тобто виконане в товстій стінці, але із загостренням вхідної кромки із зовнішнього боку. Струмінь, відриваючись від кромки отвору, трохи стискується (мал.5.2, а). Такий стиск обумовлений рухом рідини від різних напрямків, у тому числі й від радіального руху по стінці, до осьового руху в струмені.

Мал. 5.2. Витікання через круглий отвір

Ступінь стиску оцінюється коефіцієнтом стиску.

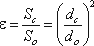
де S_с і S_о - площі поперечного переріза струменя й отвору відповідно; d_с і d_о - діаметри струменя й отвору відповідно.

Швидкість витікання рідини через такий отвір

де Н - напір рідини, визначається як

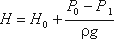
φ - коефіцієнт швидкості

де ζ - коефіцієнт Кориолиса;?- коефіцієнт опору отвору.

Витрата рідини визначається як добуток дійсної швидкості витікання на фактичну площу перерізу:

Добуток Sc і υ прийнято позначати буквою й називати коефіцієнтом витрати, тобто Q = Scυ.

У підсумку одержуємо витрату

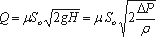
де ΔР - розрахункова різниця тисків, під дією якої відбувається витікання.

За допомогою цього вираження вирішується основне завдання - визначається витрату.

Значення коефіцієнта стиску ε, опору R, швидкості υ і витрати Q для круглого отвору можна визначити по емпірично побудованих залежностях. На мал.5.3 показані залежності коефіцієнтів ε, φ і υ від числа Рейнольдса, підрахованого для ідеальної швидкості

де ν - кінематична в'язкість.

Мал. 5.3. Залежність ε, φ і від числа Reu

Мал. 5.4. Інверсія струменів

При витіканні струменя в атмосферу з малого отвору в тонкій стінці відбувається зміна форми струменя по її довжині, що називається інверсією струменя (мал.5.4). Обумовлюється це явище в основному дією сил поверхневого натягу на криволінійні струмки, що випливають, і різними умовами стиску по периметру отвору. Інверсія найбільше проявляється при витіканні з некруглих отворів.

Дата добавления: 2014-01-07