
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Умовні ймовірності. Незалежність подій
|
|
|
|
Лекції 3,4.
Досить часто доводиться розглядати ймовірність події А за умови, що мала місце деяка інша подія В. Така ймовірність називається умовною й позначаються Р(А / В).
Приклад. Кинуто дві гральні кістки. Чому дорівнює ймовірність того, що сума очок, що випали, дорівнює 8, якщо відомо, що ця сума є парним числом?
Нехай А - сума очок, що випали, дорівнює 8,
В - сума очок, що випали, парне число.
Знайдемо спочатку ймовірність Р(А) за класичним означенням. Число всіх можливих наслідків експерименту n =6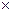 6=36, а сума очок, рівна 8, випаде в наступних комбінаціях: (2,6), (3,5), (4,4), (5,3), (6,2). У такий спосіб m =5 і Р(А) =
6=36, а сума очок, рівна 8, випаде в наступних комбінаціях: (2,6), (3,5), (4,4), (5,3), (6,2). У такий спосіб m =5 і Р(А) =  .
.
Тепер обчислимо ймовірність події А за умови, що наступила подія В. У цьому випадку можливі наслідки експерименту становлять комбінації, за яких сума очок, що випали, - парне число, таких комбінацій - 18, тому m = 5, n = 18, а умовна ймовірність Р(А / В) =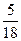 .
.
Дві події А и В називаються незалежними, якщо настання одного з них не впливає на ймовірність настання іншого, іншими словами, якщо умовна ймовірність дорівнює безумовної, Р(А / В) = Р(А). У противному випадку події вважають залежними. Так, у наведеному вище прикладі, події А і В є залежними.
Події А ,А
,А , …, А
, …, А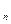 називаються незалежними у сукупності, якщо для будь-якого А
називаються незалежними у сукупності, якщо для будь-якого А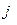 з їх числа й будь-якої підмножини даної сукупності, що не змістить події А
з їх числа й будь-якої підмножини даної сукупності, що не змістить події А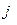 , подія А
, подія А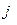 і добуток подій з підмножини взаємно незалежні.
і добуток подій з підмножини взаємно незалежні.
Розглянемо приклад. Тетраедр, три грані якого пофарбовані відповідно в червоний, зелений і синій кольори, а четверта грань містить всі три кольори, кидається навмання на площину. Події А, В, С полягають у тому, що тетраедр упав на грань, що містить відповідно червоний, зелений або синій кольори.
Безумовні ймовірності Р(А) = Р(В) = Р(С) =  ,
,
умовні ймовірності Р(А/В) = Р(А/С) = Р(В/С) = Р(С/А) = Р(В/А) = .
.
Отже попарно події незалежні, однак Р(А/ВС) = 1, а це свідчить про те що в сукупності події залежні.
Розглянемо формули, які використовуються для обчислення ймовірностей складних подій. Складною подією називається спостережувана подія, виражена через інші спостережувані у тому же експерименті події за допомогою допустимих алгебраїчних операцій.
Формула додавання. Для довільних подій А и В справедливе співвідношення
Р(А+В) = Р(А) + Р(В) - Р(АВ)
Для довільного скінченного числа подій формула додавання має вигляд:
Р(А +А
+А +…+А)
+…+А)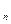 =Р(А
=Р(А )+ Р (А
)+ Р (А )+…+ Р(А
)+…+ Р(А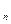 )-Р(А
)-Р(А А
А )-Р(А
)-Р(А А
А )-…- Р(А
)-…- Р(А А
А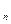 )+Р(А
)+Р(А А
А А
А )+Р(А
)+Р(А А
А А
А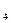 )+…+Р(А
)+…+Р(А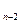 А
А А
А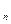 )-… (-1)
)-… (-1)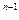 Р(А
Р(А А
А …А)
…А)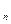 .
.
Для неспільних подій імовірність суми подій дорівнює сумі ймовірностей цих подій, тобто
Р(А +А
+А +…+А)
+…+А)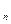 = Р(А
= Р(А )+ Р (А
)+ Р (А )+ … + Р(А
)+ … + Р(А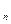 )
)
Формула множення. Для довільних подій А і В
Р(АВ) = Р(А) Р(B/A)=P(B)P(A/B.
Формула справедлива, якщо Р(А) > 0, P(B) > 0, і дозволяє обчислювати ймовірність здійснення обох подій А и В у тих випадках, коли умовна ймовірність вважається відомою або визначається методом допоміжного експерименту.
Для довільного скінченного числа подій формула множення має вигляд:
Р(А А
А …А)
…А)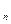 =Р(А
=Р(А ) Р(А
) Р(А / А
/ А )Р(А
)Р(А /А
/А А
А )Р(А
)Р(А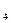 /А
/А А
А А
А )…Р(А
)…Р(А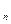 /А
/А А
А …А)
…А) .
.
Для незалежних у сукупності подій імовірність добутку подій дорівнює добутку їхніх імовірностей, тобто
Р(А А
А …А)
…А)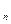 = Р(А
= Р(А А
А …А)
…А)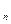 .
.
Приклад 4. В умовах експерименту, розглянутого в прикладі 3 знайти ймовірності того, що серед обраних виробів виявиться:
а) не більше одного бракованого;
б) хоча б одне браковане.
Нехай подія А - серед обраних виробів не більше одного бракованого,
Розглянемо події: А - серед обраних виробів - жодного бракованого,
- серед обраних виробів - жодного бракованого,
А - серед обраних виробів - один бракований.
- серед обраних виробів - один бракований.
Тоді А = А + А
+ А , причому А
, причому А , А
, А - несумісні. За формулою додавання шукана ймовірність Р(А) =Р(А
- несумісні. За формулою додавання шукана ймовірність Р(А) =Р(А + А
+ А ) =Р(А
) =Р(А ) +Р(А
) +Р(А ),
),
Р(А ) =
) =
 =
= 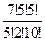 =
=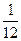 , Р(А
, Р(А ) =
) = 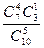 =
=  =
=  ,
,
Р(А) = 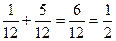
Нехай подія В - серед обраних виробів хоча б один бракований.
Можна розв’язати цю задачу за допомогою формули додавання, але розв’язок розв’язок буде значно простіше, якщо перейти до протилежної події  - серед обраних виробів немає бракованих.
- серед обраних виробів немає бракованих.
 = А
= А , Р(
, Р( ) = Р (А
) = Р (А ) =
) = 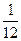 , Р(В) = 1 - Р(
, Р(В) = 1 - Р( ) = 1 -
) = 1 - 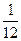 =
= 
Приклад 5. Визначити ймовірність того, що обраний навмання виріб є першосортним, якщо відомо, що 5% всієї продукції є браком, а 80% не бракованих виробів задовольняють вимогам 1-го сорту.
Позначимо А - обраний виріб є не бракованим,
В - обраний виріб задовольняє вимогам 1-го сорту,
тоді АВ - обраний виріб є першосортним, а шукана ймовірність
Р(АВ) = Р(А)Р(В/А) =  ,
,
тут Р(А) = 1 - 0,05 = 0,95, Р(В/А) = 0,8.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1162; Нарушение авторских прав?; Мы поможем в написании вашей работы!