
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формула повної ймовірності
|
|
|
|
Приклад 6. Нехай в одному із трьох ящиків знаходиться 3 білих і 2 чорних кулі, у другому - 2 білі й 3 чорних, у третьому - тільки білі кулі. З навмання обраного ящика витягають одну кулю. Знайти ймовірність того, що він білого кольору.
Позначимо через А подію, яка полягає в тому, що обрана куля білого кольору. Ймовірність цієї події залежить від того, з якого ящика обрана куля. Розглянемо події:
H - куля взята з першого ящика,
- куля взята з першого ящика,
H - куля взята із другого ящика,
- куля взята із другого ящика,
H - куля взята із третього ящика.
- куля взята із третього ящика.
Події H , H
, H , H
, H - несумісні, тоді подія А можна представити у вигляді суми добутків
- несумісні, тоді подія А можна представити у вигляді суми добутків
А= H А + H
А + H А + H
А + H А
А
Застосовуючи формули додавання й множення одержимо,
Р(А) = Р(H А + H
А + H А + H
А + H А) = Р(H
А) = Р(H А) + Р(H
А) + Р(H А) + (H
А) + (H А) =
А) =
Р(H )Р(А/ H
)Р(А/ H ) + Р(H
) + Р(H )Р(А/ H
)Р(А/ H ) + Р(H
) + Р(H )Р(А/ H
)Р(А/ H ) =
) =
Це і є формула повної ймовірності. Запишемо її в загальному виді. Нехай подія А може відбутися тільки разом з однією з подій H , H
, H , …, H
, …, H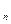 , які утворюють повну групу подій (гіпотез).
, які утворюють повну групу подій (гіпотез).
Ймовірність Р(А) визначається за формулою повної ймовірності
Р(А) = Р(H
Р(H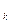 )P(A/ H
)P(A/ H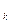 ), де
), де  Р(H
Р(H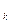 ) = 1.
) = 1.
Приклад 7. На двох автоматичних верстатах виготовляються однакові валики. Імовірність виготовлення валика вищого сорту на першому верстаті дорівнює 0,95, а на другому - 0,80. Виготовлені на обох верстатах не розсортовані валики перебувають на складі, серед них валиків, виготовлених на першому верстаті, у три рази більше, ніж на другому. Визначити ймовірність того, що навмання взятий валик виявиться вищого сорту.
Позначимо А - подію, яка полягає у тому, що взятий навмання валик виявиться вищого
сорту;
B - подія, яка полягає у тому, що взятий навмання валик
- подія, яка полягає у тому, що взятий навмання валик
зроблений на першому верстаті;
B - подія, яка полягає у тому, що валик зроблений на другому
- подія, яка полягає у тому, що валик зроблений на другому
верстаті.
Застосувавши формулу повної ймовірності одержимо:
Р(А) = Р(В )Р(А/ В
)Р(А/ В ) + Р(В
) + Р(В )Р(А/ В
)Р(А/ В ).
).
Оскільки валиків, зроблених на першому верстаті, в 3 рази більше, ніж на другому, то Р(В ) =
) =  , Р(В
, Р(В ) =
) =  .
.
У задачі дані умовні ймовірності:
Р(А/ В ) = 0,92, Р(А/ В
) = 0,92, Р(А/ В ) = 0,80.
) = 0,80.
Шукана ймовірність
Р(А) = 
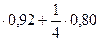 = 0,89.
= 0,89.
Формули Байеса.
В умовах Приклада 6, обрана з ящика куля, виявилася білого кольору. Знайти ймовірність того, що куля була взята із третього ящика.
Це задача відрізняється тим, що відома подія, яка наступила в результаті експерименту: Ця подія А – витягнута куля білого кольору. Потрібно знайти ймовірність гіпотези за умови, що наступила подія А, тобто Р(Н /А).
/А).
Розглянемо ймовірність Р(А Н ), за формулою множення
), за формулою множення
Р(А Н ) = Р(А)Р(Н
) = Р(А)Р(Н /А) = Р(Н
/А) = Р(Н )Р(А/ Н
)Р(А/ Н ).
).
З останньої рівності виразимо шукану ймовірність
Р(Н /А) =
/А) = 
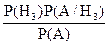
 , де Р(А) - повна ймовірність події А.
, де Р(А) - повна ймовірність події А.
Отримана рівність і є формула Байеса для Н. Аналогічно можна одержати формули для гіпотез H
Аналогічно можна одержати формули для гіпотез H і H
і H .
.
Використовуючи результати Приклада 6, одержимо
Р(Н /А) =
/А) = 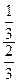 =
=  .
.
Запишемо формули Байеса в загальному виді:
Р(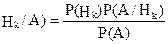 , Р(А) – повна ймовірність події А,
, Р(А) – повна ймовірність події А,
 Р(H
Р(H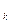 ) = 1, k =
) = 1, k = 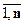 .
.
Приклад 8. В умовах Приклада 7, взятий навмання валик виявився вищого сорту. Визначити ймовірність того, що він зроблений на першому верстаті.
Використовуючи позначення Приклада 7, за формулою Баейса одержимо:
Р(В /А) =
/А) = 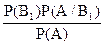 =
= 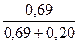 = 0,76.
= 0,76.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 508; Нарушение авторских прав?; Мы поможем в написании вашей работы!