Математичне сподівання

Числові характеристики випадкової величини.

Лекція 6.

Випадкові величини крім законів розподілу можуть описуватися також числовими характеристиками.

Математичним сподіванням М (x) випадкової величини називається її середнє значення.

Математичне сподівання дискретної випадкової величини обчислюється за формулою

М (x) =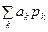, (1)

де 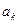– значення випадкової величини, 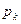- їх ймовірності.

Розглянемо властивості математичного сподівання:

1. Математичне сподівання константи дорівнює самій константі

М (С) = С

2. Якщо випадкову величину помножити на деяке число k, то й математичне сподівання помножиться на це ж число

М (kx) = kМ (x)

3. Математичне сподівання суми випадкових величин дорівнює сумі їх математичних сподівань

М (x₁ + x₂ + … + x_n) = М (x₁₎ + М (x₂₎ +…+М (x_n)

4. М (x₁ - x₂₎ = М (x₁₎ - М (x₂₎

5. Для незалежних випадкових величин x₁, x₂, … x_n математичне сподівання добутку дорівнює добутку їхніх математичних сподівань

М (x₁, x₂, … x_n ) = М (x₁₎ М (x₂₎ … М (x_n)

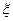6. М ((- М (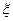)) = М (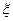) - М (М(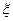)) = М (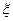) - М ((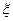) = 0

Обчислимо математичне сподівання для випадкової величини із Приклада 11.

М (x) = = .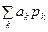

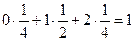Приклад 12. Нехай випадкові величини x₁, x₂ задані відповідно законами розподілу:

Таблиця 2. Закон розподілу x₁

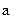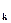
	- 0,1	- 0,01		0,01	0,1
р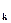	0,1	0,2	0,4	0,2	0,1

Таблиця 3. Закон розподілу x₂

b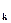	- 20	- 10
р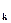	0,3	0,1	0,2	0,1	0,3

Обчислимо М (x₁₎ і М (x₂₎

М (x₁) = (- 0,1) 0,1 + (- 0,01) 0,2 + 0 · 0,4 + 0,01 · 0,2 + 0,1 · 0,1 = 0

М (x₂) = (- 20) 0,3 + (- 10) 0,1 + 0 · 0,2 + 10 · 0,1 + 20 · 0,3 = 0

Математичні сподівання обох випадкових величин однакові - вони дорівнюють нулю. Однак характер їхнього розподілу різний. Якщо значення x₁ мало відрізняються від свого математичного сподівання, то значення x₂ у великому ступені відрізняються від свого математичного сподівання, і ймовірності таких відхилень не малі. Ці приклади показують, що за середнім значенням не можна визначити, які відхилення від нього мають місце як у меншу, так і в більшу сторону. Так при однаковій середній величині опадів, що випадають у двох місцевостях, за рік не можна сказати, що ці місцевості однаково сприятливі для сільськогосподарських робіт. Аналогічно по показнику середньої заробітної плати не можливо судити про питому вагу високо- і низькооплачуваних працівників. Тому, запроваджується числова характеристика – дисперсія D (x), що характеризує міру відхилення випадкової величини від свого середнього значення:

D (x) = M (x - M (x))² . (2)

Дисперсія - це математичне сподівання квадрата відхилення випадкової величини від математичного сподівання. Для дискретної випадкової величини дисперсія обчислюється за формулою:

D (x) = 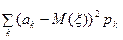= 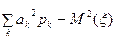(3)

Із означення дисперсії випливає, що D (x)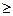0.

Властивості дисперсії:

1. Дисперсія константи дорівнює нулю

D (C) = 0

2. Якщо випадкову величину помножити на деяке число k, то дисперсія помножиться на квадрат цього числа

D (kx) = k² D (x)

3. D (x) = М (x²⁾ – М² (x)

4. Для попарно незалежних випадкових величин x₁, x₂, … x_n дисперсія суми дорівнює сумі дисперсій.

D (x₁ + x₂ + … + x_n) = D (x₁) + D (x₂) +…+ D (x_n)

Обчислимо дисперсію для випадкової величини із Приклада 11.

Математичне сподівання М (x) = 1. Тому за формулою (3) маємо:

D (x) = (0 – 1)²·1/4 + (1 – 1)²·1/2 + (2 – 1)²·1/4 =1/2

Відзначимо, що дисперсію обчислювати простіше, якщо скористатися властивістю 3:

D (x) = М (x²) – М² (x).

Обчислимо дисперсії для випадкових величин x₁, x₂ із Приклада 12 за цією формулою. Математичні сподівання обох випадкових величин дорівнюють нулю.

D (x₁) = (0,1)²· 0,1+(0,01)²· 0,2+ (0,01)²· 0,2+(0,1)²· 0,1 = 0,001 + 0,00002 + 0,00002 + 0,001 = = 0,00204

D (x₂) = (-20)² · 0,3 + (-10)² · 0,1 + 10² · 0,1 + 20² · 0,3 = 240 +20 = 260

Чим ближче значення дисперсії до нуля, тим менше розкид випадкової величини навколо середнього значення. Величина 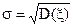називається середньоквадратичним відхиленням.

Модою випадкової величини x дискретного типу Md називається таке значення випадкової величини, якому відповідає найбільша ймовірність.

Дата добавления: 2014-01-07