
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Щільність розподілу
|
|
|
|
Неперервні випадкові величини.
Лекція 7,8.
.
Аналогічно можна показати, що математичне сподівання й дисперсію відповідно рівні 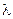 ,
,
М (x) = 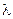 , D (x) =
, D (x) = 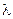 .
.
Закон Пуассона називають законом рідких подій.
Щільність розподілу ймовірностей f(x) характеризує ймовірність попадання випадкової величини в деякий інтервал. Ця ймовірність дорівнює площі фігури, розташованої між віссю абсцис і графіком функції f(x) на інтервалі 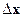 (Рисунок 8). Зазначимо, що функція f(x) =
(Рисунок 8). Зазначимо, що функція f(x) =
 .
.

Рисунок 8. Щільність розподілу ймовірностей f(x)
Щільність розподілу має наступні властивості:
1. f (x) >0
2. 
3. p(a
4. f(x) = 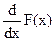 в точках неперервності функції f(x).
в точках неперервності функції f(x).
Поняття функції розподілу, математичного сподівання й дисперсії мають такий же смисл, як у дискретному випадку, а обчислюються відповідно за формулами (6) - (8).
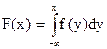 (6)
(6)
M (x) = 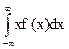 (7)
(7)
D ( x) = 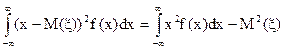 (8)
(8)
Приклад 13. Випадкова величина 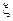 , що розподілена за законом, який визначається щільністю розподілу ймовірностей виду
, що розподілена за законом, який визначається щільністю розподілу ймовірностей виду
f (x) = 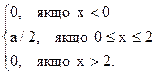

Знайти параметр a, F(x), M (x), D ( x).
Параметр a знайдемо із властивості  , інтеграл
, інтеграл 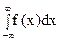 розіб'ємо на суму трьох інтегралів
розіб'ємо на суму трьох інтегралів
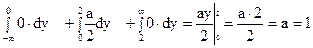
Намалюємо графік щільності розподілу f (x) (Рисунок 9)

Рисунок 9. Графік щільності розподілу f (x)
Обчислимо функцію розподілу, для цього розглянемо інтервали  .
.
1. х Î (- ∞, 0) 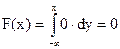 ,
,
2. х Î [0, 2] 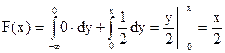 ,
,
3. х 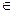 (2,
(2,
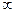 )
)  .
.
Графік функції наведений на Рисунку 10.
Обчислимо математичне сподівання й дисперсію:


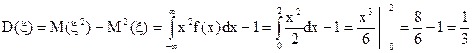
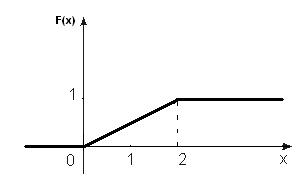
Рисунок 10. Графік функції розподілу.
Модою випадкової величини x неперервного типу Md, називається дійсне число - точка максимуму щільності розподілу ймовірностей f(x).
Медіаною випадкової величини x неперервного типу Mn називається дійсне число, що задовольняє рівняння
F(x) =  .
.
Квантилью порядка р розподілу випадкової величини x неперервного типу називається дійсне число 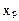 , що задовольняє рівняння р
, що задовольняє рівняння р = р
= р
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1772; Нарушение авторских прав?; Мы поможем в написании вашей работы!