Приклади розподілів безперервної випадкової величини

1. Рівномірний розподіл.

Випадкова величина x неперервного типу називається розподіленою рівномірно на відрізку [a,b], якщо її щільність розподілу має від:

f(x) = (9)

Обчислимо математичне сподівання й дисперсію: ,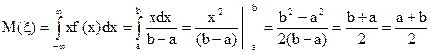

=

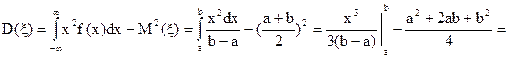
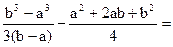
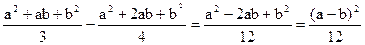
Розглянутий в Прикладі 13 розподіл є рівномірним при a = 0 і b = 1.

2. Показниковий (експонентний) розподіл:

Випадкова величина x називається розподіленою за показниковим (експонентним) законом з параметром 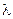>0, якщо вона неперервного типу і її щільність розподілу задається формулою

f(x) = 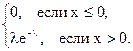(10)

Графік функції наведений на Рисунку11.

Рисунок 11. Щільність показового (експонентного) розподілу

Математичне сподівання й дисперсія відповідно рівні:

M (x) = 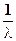, D (x)=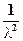

3. Закон нормального розподілу.

Випадкова величина називається розподіленою за нормальним законом з параметрами а й 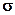>0, якщо щільність розподілу ймовірностей має вигляд

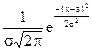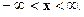
f(x) = , (11)

Для того, щоб побудувати графік цієї функції, проведемо її дослідження. Обчислимо похідну

.

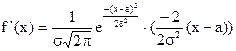При x < a 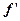> 0, отже на інтервалі 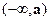функція зростає, а при x > a 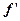< 0, - функція спадає. У точці x = a – функція має максимум. Графік функції наведений на Рисунку 12.

Важливе значення в прикладних задачах має окремий випадок щільності нормального розподілу при a = 0 і 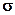=1

. (12)

Це, так званий, стандартний нормальний розполіл. Функція (12) - парна, тобто

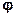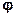(-x) = (x).

Для значень цієї функції є таблиці (Додаток 1).

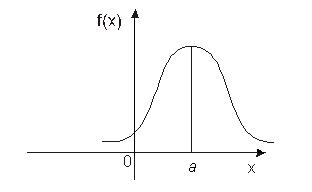
Рисунок 12. Щільність нормального розподілу.

Обчислимо математичне сподівання й дисперсію:

; ; .

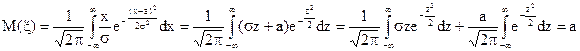
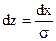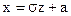При обчисленні інтегралів використані властивості:

1) 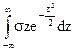= 0, як інтеграл від непарної функції в симетричних межах;

2) 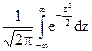=1, як інтеграл від щільності нормального розподілу з параметрами a = 0 і 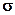= 1 (властивість 2 функції щільності розподілу).

Аналогічно можна показати, що D (x) =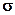². Параметри a і 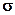збігаються з основними характеристиками розподілу. Надалі, якщо щільність розподілу випадкової величини має вигляд (11), то для стислості будемо записувати x ~ N ().

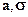Ймовірність попадання випадкової величини x в інтервал 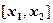обчислюється за формулою

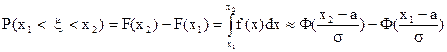, (13)

де 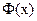- функція Лапласа

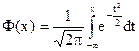, ( 14)

функція нормального розподілу N(0,1),для цієї функції є таблиці (Додаток 2).

Відзначимо, що

Ф(-x) = 1 - Ф(x) (15)

Приклад 14. Коробки із шоколадом упаковують автоматично. Їхня середня маса дорівнює 1,06 кг. Відомо, що 5 % коробок мають масу менше 1 кг. Який відсоток коробок, маса яких перевищує 940 р. (вага коробок розподілена нормально)?

В умовах задачі параметр а = 1,06, параметр 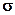-невідомий. Розглянемо випадкову величину (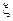- маса коробок. Потрібно визначити

p (x > 0,94), тобто p (x > 0,94) = p (0,94 < x < + ∞)

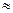
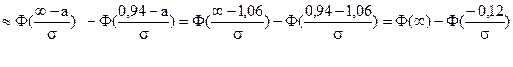
З таблиці Додатка 2 визначимо 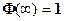, за формулою (14) маємо

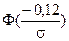= 1-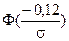, тоді p (0,94 < x < + ∞) 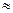1-1+= .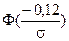

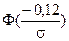Параметр 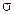знайдемо з умови р (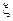< 1) = 0,5

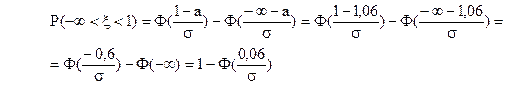
тобто 1-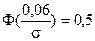 звідки одержимо ) = 0,95.

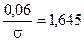За таблицею Додатка 3 визначимо = 1,645, тоді з рівності знайдемо значення . Остаточно одержимо

.

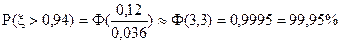4. Розподіл Парето

Розподіл Парето використовується при вивченні розподілу доходів, що перевищують деякий граничний рівень x₀.

f(x) = 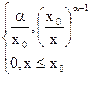x₀ < x < ∞, α > 0, х₀ > 0 – параметри розподілу, (16)

При 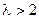математичне сподівання і дисперсія визначаються за формулами

M(ξ)=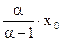, D(ξ)=.

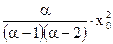Дата добавления: 2014-01-07